René Descartes Descartes et les Mathématiques

Calcul différentiel appliqué à la recherche d'extremums

Capes externe de mathématiques 2007 - Épreuve sur dossier

Sommaire

Problème d'optimisation :
Recherche d'un volume maximal avec une surface minimale

3. Casserole
Découper une casserole dans une plaque
4. Parallélépipède rectangle
Boite à chaussures

Technique GéoPlan : dans ces exercices est utilisée une seule figure avec deux cadres : le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction.

1. Le canal ouvert

figure geometrique et optimisation d'une fonction - profil d'un canal - copyright Patrice Debart 2008

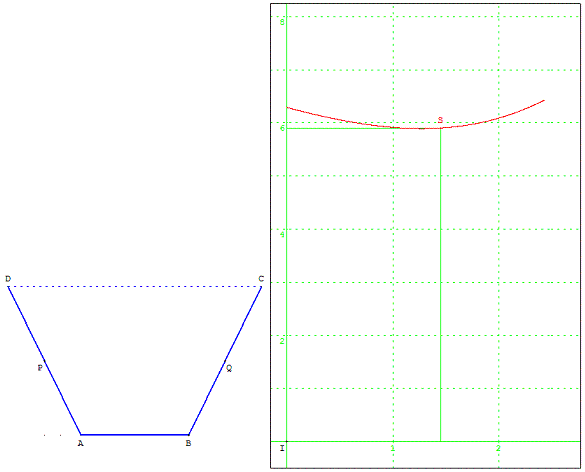
Un canal ABCD a une section en forme de trapèze isocèle de hauteur h et d'aire S fixées. La petite base AB = a et la grande base CD = b.

Comment choisir a pour que le bétonnage des bords et du fond du canal soit optimal, soit DA + AB + BC minimal.

Déplacer le point A pour trouver le minimum.

Déplacer P, milieu de [AD], pour modifier les données h et S.

Télécharger la figure GéoPlan canal.g2w

Calculs

S = h × (a+b)/2 d'où a+b = 2S/h = q. Soit b = q − a.

p = DA + AB + BC = AB + 2 DA

DA² = ((b−a)/2) + h² = (q/2 − a)² + h²

donc p = a + 2 rac[ (q/2 − a)² + h²]

Je ne sais pas étudier le minimum de cette fonction de la variable a. Il doit y avoir une astuce à retrouver dans les manuels.

Problème d'optimisation : maximisation de volume avec une surface minimale

2. Cylindre

Optimiser l'aire d'un cylindre : le cylindre « économique » a un diamètre égal à sa hauteur.

Première question de l'épreuve de physique du concours de l'X de l'année 2004 en MP.

Indications

On nomme h la hauteur du cylindre, r son rayon.
À volume V fixé, on cherche les valeurs de r et h telles que l'aire du fond et du côté du cylindre soit minimale.

Il suffit d'exprimer le volume en fonction de r et h : V = πr²h,
de calculer h dans cette formule : h = V/(πr²).
Puis exprimer l'aire A en fonction de r et h : A = 2πr² + 2πrh.
On substitue h pour exprimer l'aire en fonction de r et du volume V : A = 2πr² + 2V/r.

En classe de première, on utilise la dérivée A’ = dA/dr : A’ = 4 πr − 2V/r² = (4πr³ − 2V)/r².
L'aire est extrémale lorsque A’ s'annule : on obtient donc une relation entre r et V : 4 πr³ − 2V = 0, soit r³ = V/(2π).
Mais comme d'après le calcul du volume V/π = r²h, on a : h = 2r.

On a donc r = h/2 = {V/(2π)}^(1/3).

3. Casserole

a. Optimisation du volume d'une casserole

Montrer que pour un volume V donné, la casserole « économique » est celle dont le rayon est égal à la hauteur.

Indications

On nomme h la hauteur du cylindre, r son rayon.
À volume V fixé, on cherche les valeurs de r et h telles que l'aire du fond et du côté du cylindre soit minimale.

Il suffit d'exprimer le volume en fonction de r et h : V = πr²h,
de calculer h dans cette formule : h = V/(πr²).
Puis exprimer l'aire A en fonction de r et h : A = πr² + 2πrh.
On substitue h pour exprimer l'aire en fonction de r et du volume V : A = πr² + 2V/r.

En classe de première, on utilise la dérivée A’ = dA/dr : A’ = 2πr − 2V/r² = (2πr³ − 2V)/r².
L'aire est extrémale lorsque A’ s'annule : on obtient donc une relation entre r et V : 2πr³ − 2V = 0, soit r³ = V/π.
Mais comme d'après le calcul du volume V/π = πr²h, on a : h = r.

On a donc r = h = (V/π)^(1/3).

b. Découper une casserole dans une plaque

figure geometrique et optimisation d'une fonction - decouper une casserole dans une plaque - copyright Patrice Debart 2008

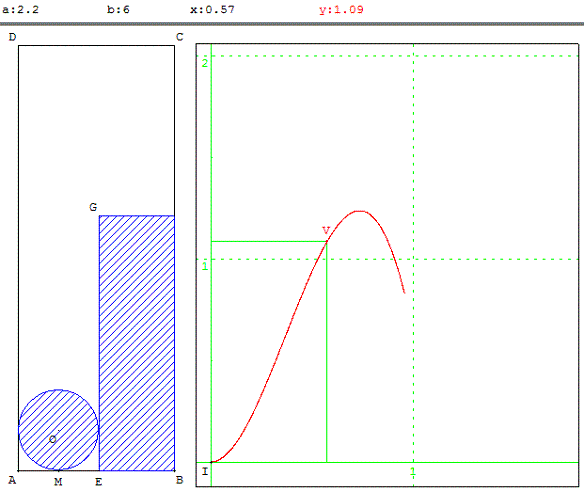
Dans une plaque rectangulaire ABCD de largeur a = AB et de longueur b = BC, on découpe le fond d'une casserole, un disque de rayon x, et un rectangle de longueur 2πx pour le bord.

Comment choisir x pour que la casserole soit de volume maximal ?

Solution : x = b/(2π) si a<b/(6π) (G est alors situé sur [CD]), sinon x = a/3.

Le problème n'a d'intérêt que lorsque la longueur b de la plaque est suffisamment grande pour que l'optimisation conduise à un bord de longueur inférieure à celle de la plaque (EG < b).

L'abscisse a/3 du maximum relatif de la fonction du troisième degré représentant le volume, V(x) = π x² (a − 2x), se trouve alors entre 0 et b/(2π), avec a < b/(6π).

Télécharger la figure GéoPlan casserole.g2w

d. Découper un cylindre dans une plaque

Dans une plaque rectangulaire ABCD de longueur a = AB et de largeur b = BC, on découpe deux disques de rayon x, et un rectangle de longueur 2 π x pour le bord d'un cylindre.

Comment choisir x pour que le cylindre soit de volume maximal ?

Les contraintes d'optimisation sont pratiquement les mêmes que pour la casserole.

Télécharger la figure GéoPlan cylindre.g2w

4. Parallélépipède rectangle (pavé droit)

On cherche les dimensions (x:longueur, y:largeur et z: hauteur) d'une boite parallélépipède rectangle qui permettent de maximiser son volume V tout en minimisant son aire S.

Bien sûr, V = xyz et S = 2(xy+yz+xz).

la solution est x = y = z = V^(1/3)

Tu peux le résoudre avec des outils de 1^ère S :

1) On fixe V=V₀ et x=x₀. On considère la fonction y → S(y)
{S(y) = 2(x₀ y + V₀/x₀ + V₀/y) }
Une étude de fonction élémentaire montre que le minimum est atteint pour y_m= rac(V₀/x₀).

2) On cherche le « minimum des minima » en étudiant la fonction x₀ → S(y_m).
Là aussi une étude élémentaire montre que le minimum est atteint pour x₀ = V₀^(1/3)

Voir : multiplicateur de Lagrange

Boite à chaussures

Optimisation du volume d'une boite

Classe de 1^ère S

figure geometrique et optimisation d'une fonction - boite a chaussures - copyright Patrice Debart 2008

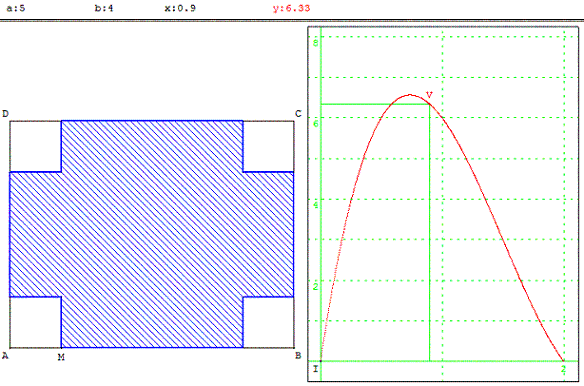
Dans une plaque rectangulaire ABCD de longueur a = AB et de largeur b = BC, on découpe dans chaque coin un carré de côté x, pour construire une boite de hauteur x.

Comment choisir x pour que la boite soit de volume maximal ?