
 Descartes et les Mathématiques
Descartes et les Mathématiques
Échelle appuyée contre un mur
Sommaire
1. Problème
2. Échelle vue de profil
3. Lieu d'un point de l'échelle
4. Lieux des barreaux d'une échelle
5. Figure interactive avec GeoGebra
1. Problème

Un problème très ancien, trouvé sur une tablette babylonienne de 2000/1800 avant J.-C. :
« Un bâton 5 unités de longueur est appuyé contre un mur. Le haut glisse d'une unité.
De combien le pied du bâton s'est-il éloigné de la base du mur ? »
Intérêt
Les élèves n'ont pas d'idée immédiate du résultat et plusieurs conjectures peuvent surgir.
La construction d'un segment de longueur constante, dont les extrémités sont mobiles sur des demi-droites perpendiculaires, nécessite l'élaboration d'une stratégie de construction.
La démonstration est accessible en classe quatrième.
Une autre version :
Une échelle de 7 m est appuyée contre un mur,
elle glisse sur le sol en restant en contact avec le mur.
Étudier le lieu du milieu de l'échelle.
2. Échelle vue de profil
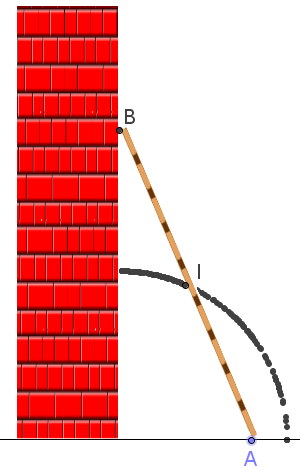
Le lieu du milieu I de [AB] est un quart de cercle de centre O de rayon égal à la moitié de la longueur de l'échelle.
Indication
OAB un triangle rectangle et le segment [IO] est la médiane de ce triangle, issue de l'angle droit, médiane égale à la moitié de la longueur de l'hypoténuse [AB].
Compétences mathématiques
Exploiter les propriétés du triangle rectangle :
– Le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse, d'où la longueur de la médiane issue de l'angle droit.
En classe de cinquième, on inscrit le triangle rectangle AOB dans un rectangle AOBC et on exploite les propriétés des diagonales.
Problème de Pappus - échelle contre un mur
Dans un repère Oxy, on considère un carré OIJK de côté a avec I sur [Ox) et J sur [Oy). Une échelle de longueur l, passant par J, est posée en A sur la demi-droite [Ox)
et s'appuie en B sur la demi-droite [Oy).
Déterminer la position de cette échelle : cela revient à calculer OA et OB en fonction de a et l.
![]() Télécharger la figure GéoPlan equerre2.g2w
Télécharger la figure GéoPlan equerre2.g2w
3. Lieu d'un point de l'échelle
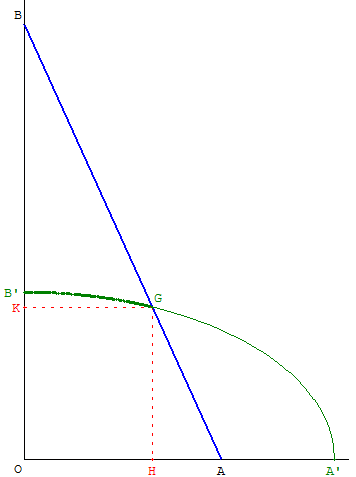
Étudier le lieu d'un point G situé sur le segment [AB].
Dans ce cas particulier, le point G est le barycentre des points pondérés (A, 1-k) et (B, k) ; avec k ≠ 0
Avec GeoGebra G est le point (1-k) A + k B
Lorsque l'on déplace le point A, on trouve un quart d'ellipse, comme lieu du point G.
Démonstration analytique - Après bac
On note a l'abscisse de A, b l'ordonnée de B et l la longueur de l'échelle. Dans le triangle rectangle OAB, on a la relation de Pythagore a2 + b2 = l2.
Soit G(x, y) un point fixe de l'échelle tel que AG = k AB (0 < k < 1).
Soit H(x, 0) et K(0, y) les projections de G sur les axes.
On a y = kb et x = (1 - k)a ; d'où a = x/(1 - k) et b = y/k.
Par substitution dans la relation de Pythagore on a :
x2/(1 - k)2 + y2/k2 = l2,
soit x2/((1 - k)l)2 + y2/(kl)2 = 1, équation d'une ellipse de sommets A’ et B’ où A’ est le point de [OA) tel que OA’ = (1 - k)l et B’ le point de [OB) tel que OB’ = kl.
![]() Télécharger la figure GéoPlan echelle_contre_mur.g2w
Télécharger la figure GéoPlan echelle_contre_mur.g2w
4. Lieux des barreaux d'une échelle
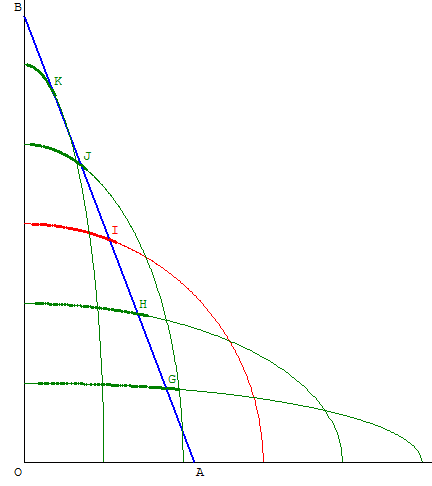
Échelle à cinq barreaux
Une échelle, de longueur 6, a cinq barreaux.
On représente les lieux des cinq barreaux à partir des points :
G barycentre des points pondérés (A, 5) et (B, 1),
avec GeoGebra saisir G = (5A + B)/6
H barycentre des points pondérés (A, 4) et (B, 2),
saisir H = (4A + 2B)/6
I milieu de [AB],
J barycentre des points pondérés (A, 2) et (B, 4), saisir J = (2A + 4B)/6
K barycentre des points pondérés (A, 1) et (B, 5), saisir K = (A + 5B)/6
Les trajectoires sont des arcs d'ellipses.
![]() Télécharger la figure GéoPlan echelle_contre_mur2.g2w
Télécharger la figure GéoPlan echelle_contre_mur2.g2w
5. Figure interactive avec GeoGebra
Une échelle de 7 m est appuyée contre un mur,
elle glisse sur le sol en restant en contact avec le mur.
étudier le lieu du milieu de l'échelle.
Lieu de point
Déplacer le point A,
appuyer sur CTRL F ou cliquer sur « Réinitialiser la construction » pour rafraéchir l'affichage du lieu de points.
![]() Figure interactive dans GeoGebraTube : échelle contre un mur
Figure interactive dans GeoGebraTube : échelle contre un mur
Table des matières
Bibliographie : Le LGD mène l'enquête, IREM de Lyon
|
|
|
|
Page no 188, créée le 24/1/2012 |