Descartes et les Mathématiques
Vitre cassée
Sommaire
1. Problème
2. Porte surmontée d'un arc de cercle
3. Porte surmontée d'une demi-ellipse
4. Porte surmontée d'une anse de panier
1. Problème
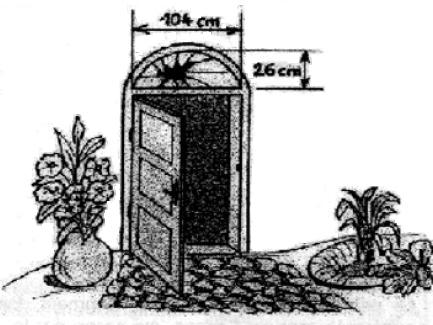
On doit remplacer le carreau cassé au-dessus d'une porte d’entrée.
Comment le vitrier peut-il faire pour construire ce carreau ?
On utilise le logiciel GeoGebra :
On crée trois nombres :
• grand axe, largeur de l'ellipse : l = 1,04,
• la flèche : f = 0,26
• et h la hauteur de la porte (ajustée à la taille de l'écran).
2. Porte surmontée d'un arc de cercle
Déterminer la position du centre du cercle :
• technique de l'intersection de deux médiatrices de [AB] et de [BF], où F est le milieu de l'arc AB) ;
• Les triangles rectangles OFB et JFI sont semblables (côtés perpendiculaires).
Déterminer le rayon r du cercle et l'angle au centre de l'arc AB :
Des rapports de similitudes IF/BF = JF/ OF, avec a = l/2 = OB, f = OF et d = BF
où Pythagore dans OFB donne d2 = a2 + f2,
on trouve IF/d = (d/2)/f soit r = IF = d2/(2f) = (a2 + f2)/(2f).
Avec α = AÎB, l'aire de la vitre est égale à l'aire πr2(α/360) du secteur circulaire IAB moins l'aire 
IO × AB du triangle IAB.
Figure dans GeoGebraTube : porte surmontée d'un arc de cercle
3. Porte surmontée d'une demi-ellipse
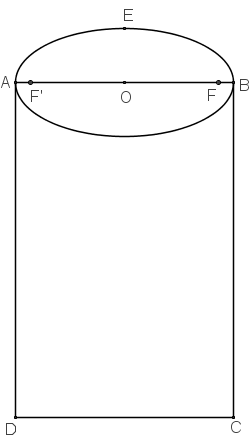
Avec GeoGebra il est facile de tracer l'ellipse de grand axe AB = l = 1,04 = 2a,
de demi-axe OF = f = 0,26 en plaçant sur [AB] les foyers F et F’ d'abscisses c = rac(a2 - f 2) et -c.
L'aire de la demi-ellipse est égale à π af.
Figure dans GeoGebraTube : porte surmontée d'une demi-ellipse
4. Porte surmontée d'une anse de panier
Cintre surbaissé à trois centres
WikiPédia : Arc (architecture), photo : Miroslav Zlevský
La Porte est certainement placée sous une voûte. Depuis l'antiquité avec Héron d'Alexandrie,
on utilise l'anse de panier pour les dessiner.
Une anse de panier est une courbe destinée à remplacer une demi-ellipse,
courbe formée d'un en nombre impair d’arcs de cercle, souvent utilisée en architecture pour réaliser une voûte.
Sa forme se rapproche de celle de l'ellipse.
Construction d'une anse de panier
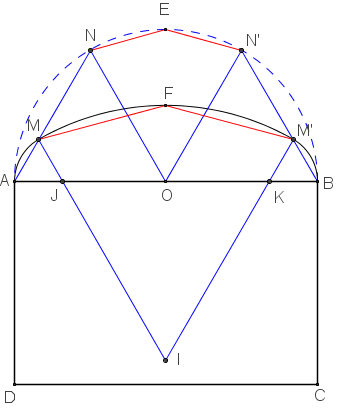
Nous utilisons la méthode de Huyghens, de partage en trois arcs de cercle correspondant à des angles au centre de 60°,
arcs qui facilitent les calculs.
Sur le grand axe [AB], de longueur 2a, décrivons une demi-circonférence de milieu E.
Partageons ce demi-cercle en trois arcs de même longueur aux points N et N’.
Par le sommet F de la flèche, traçons les parallèles à (EN) et (EN’). Elles coupent [AN] et [AN’] en M et M’.
Les parallèles à (ON) et (ON’) coupent [AB] en J et K et se coupent en I.
Les points J, I et K sont les centres de trois arcs cherchés.
La surface de la vitre se calcule facilement avec l'aire des trois secteurs circulaires, d'angles 60°
(mesurant 
r2 avec r = JM ou r = IM), diminuée de l'aire du triangle équilatéral IJK.
Figure dans GeoGebraTube : porte surmontée d'une anse de panier
Table des matières
Mobile friendly
WikiPédia : anse de panier
Page no 186, créée le 1/12/2011
mise à jour le 12/11/2014