Descartes et les Mathématiques

La géométrie du triangle rectangle

Cercles inscrits et théorème de Feuerbach

Sommaire

1. Construction des cercles inscrit et exinscrits dans un triangle
    – Points de Feuerbach
2. Point de Feuerbach

3. Utilisation de l'espace dans la résolution d'un problème plan
    – Losanges de côtés r

Avec GéoPlan, dans d'autres pages du site

Le triangle rectangle - paragraphes précédents :
     trois cercles inscrits dans le triangle rectangle

Théorème de Feuerbach (triangle quelconque)

Google friendly

1. Point de Feuerbach dans un triangle rectangle

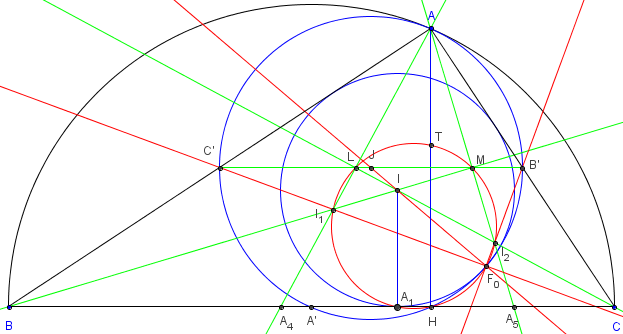
Théorème de Feuerbach-Ayme

Soit ABC un triangle rectangle en A, H le pied de la hauteur de ABC sur (BC), I₁et I₂ les centres des cercles inscrits dans les triangles AHB et AHC, et F_e le point de Feuerbach « inscrit » du triangle ABC ; alors les droites (C’I₁) et (B’I₂) sont orthogonales et se coupent au point de Feuerbach.
Le cercle de diamètre [I₁I₂] passe par F_e.

Remarque : outre le point de Feuerbach, le cercle de diamètre [I₁I₂] contient le pied H de la hauteur issue de A, le point de contact A₁ du cercle inscrit dans ABC avec le côté (BC) et les points d'intersection des bissectrices des angles aigus B et C avec la droite des centres (B’C’).
Ces deux derniers points sont aussi situés sur les bissectrices en A des triangles AHB et AHC.

Le point T, situé sur la hauteur [AH] à une distance r de A, est aussi situé sur ce cercle ;
r est le rayon du cercle inscrit.

Soit A₄ et A₅ les points d'intersection des bissectrices des angles aigus B et C avec le côté (BC).
A₁ est le milieu de [A₄A₅] et le point A₁ est situé à une distance r de A₄ et de A₅.

Figure interactive dans GeoGebraTube : point de Feuerbach d'un triangle rectangle

2. Utilisation de l'espace pour un problème plan

Losanges de côtés r

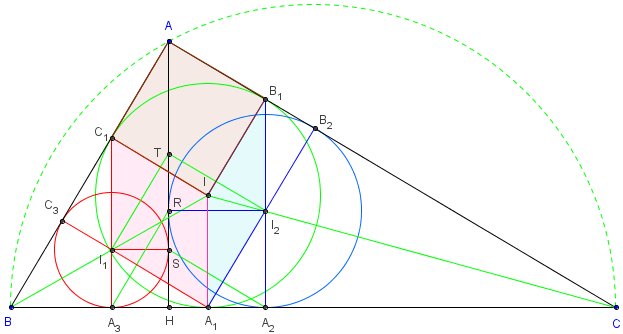
Les rayons (I₁C₃) et (I₂B₂) sont concourants en A₁.

A₃, I₁ et C₁ sont alignés, de même A₂, I₂ et B₁ sont alignés.

A₁I₂TI₁ et IB₁AC₁ sont deux carrés de côtés r.

Cette figure permet d'imaginer un cube A₁I₂TI₁IB₁AC₁. Les segments de la représentation ayant pour longueur r.

Les droites (AI) et (I₁I₂) sont perpendiculaires.

Les démonstrations se font avec les triangles rectangles HSA₂ et HRA₃, de côtés de longueurs r₁ et r₂ et d'hypoténuse r, semblable à ABC.

Par exemple montrons que le point A₁est situé sur la droite (I₁C₃) :
Dans le losange A₁IC₁C₃, on a A₁I = I₁C₁= r ; le triangle rectangle C₃C₁I₁ est inversement isométrique à HRA₃, donc C₁C₃ = r₂.

Soit A’ le point d'intersection de (BC) et (I₁C₃). A₃I₁A’ est un triangle rectangle de côté r₁ et est, par côtés parallèles, isométrique à HSA₂. Donc A₃A’ = r₂.
Par rapport aux tangentes en B du cercle inscrit (c₁) on a BA’ = BA₃ + A₃A’ = BA₃ + r₂ = BC₃ + r₂ = BC₃ + C₃C₁ = BC₁.
Par rapport aux tangentes en B du cercle inscrit (c) on a BC₁ = BA₁.
On a donc BA’ = BA₁. Les points A’ et A₁ sont confondus.

On montre de même que le point A₁est situé sur la droite (I₂B₂).

Remarque : dans cette figure, on retrouve les calculs de la hauteur : h = HS + ST + TA = r₁ + r₂ + r
ou h = HR + RT + TA = r₂ + r₁ + r.

Figure interactive dans GeoGebraTube : trois cercles inscrits dans un triangle rectangle

Figures réalisées à partir des pages de F Marsal : triangle rectangle et cercles inscrits ; où l'on trouvera les démonstrations.

3. Construction des cercles inscrit et exinscrits dans un triangle

Points de Feuerbach

Légende :
En vert : les côtés du triangle
En bleu : les bissectrices intérieures
En rouge : les bissectrices extérieures
En violet : les trois cercles exinscrits
En orange : le cercle inscrit

Figure interactive dans GeoGebraTube : théorème de Feuerbach

Théorème de Feuerbach

Dans un triangle, le cercle d'Euler est tangent au cercle inscrit et aux trois cercles exinscrits.

Indications

Comme son nom l'indique, ce théorème a été découvert en 1822 par Feuerbach (1800-1834), puis démontré par M'Clelland en 1891 et Lachlan en 1893.

Les quatre points de contact entre le cercle d'Euler et le cercle inscrit et les trois cercles exinscrits s'appellent les points de Feuerbach.

Les trois points F₁, F₂ et F₃ de tangence des cercles exinscrits forment le triangle de Feuerbach du triangle donné.

Le centre I du cercle inscrit dans le triangle ABC est l'orthocentre du triangle I₁I₂I₃ (acutangle : dont les trois angles sont aigus) formé par les trois bissectrices extérieures.

Version interactive

Index triangle

La géométrie
avec GeoGebra

WikiPédia
Théorème de Feuerbach-Ayme

Page n^o 191, réalisée le 22/9/2011
mise à jour le 29/11/2013