Descartes et les Mathématiques
Travaux pratiques de géométrie avec GeoGebra : feuille de travail dynamique.
Trois cercles égaux tangents à l'intérieur d'un triangle
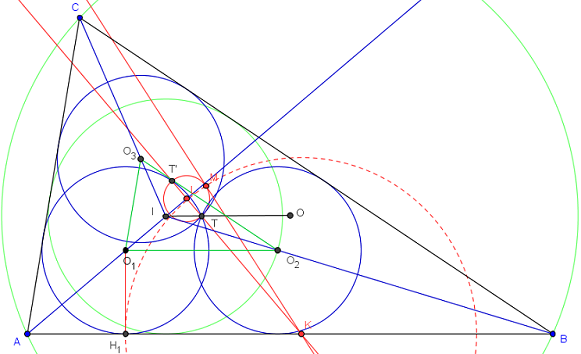
La figure suivante a été l'objet d'une question sur le forum les-mathematiques.net il a quelque temps (la question était : montrer que les points I, T et O sont alignés).
Emmanuel Moreau propose quelques questions supplémentaires, qui peuvent faire l'objet de beaux problèmes en TS spé maths.
Trois cercles de même rayon se rencontrent en un point T. À partir de ces trois cercles, on construit un triangle ABC en traçant, à l'extérieur des cercles, des tangentes communes aux cercles pris 2 à 2, comme l'indique la figure ci-dessous.
Réciproquement
Dans la figure précédente, tout est effacé sauf le triangle ABC. Il s'agit de retrouver les trois cercles « inscrits » avec leurs centres O1, O2 et O3.
On note :
I le centre du cercle inscrit dans ABC et O le centre du cercle circonscrit à ABC.
r le rayon des cercles de centres O1, O2 et O3.
R le rayon du cercle inscrit dans ABC.
R’ le rayon du cercle circonscrit à ABC.
Trouver une relation reliant ces trois rayons.
Homothétie de centre I
TO1, TO2 et TO3 sont des rayons des trois cercles inscrits, de longueur r. T est donc le centre du cercle circonscrit au triangle O1O2O3, de rayon r. L'homothétie de centre I et de rapport r/R transforme le triangle ABC en O1O2O3. Les côtés du triangle O1O2O3 sont donc parallèles à ceux du triangle ABC. L'image du cercle circonscrit à ABC est le cercle circonscrit à O1O2O3. L'image du centre O par cette homothétie est le centre T.
Recherche
Sachant que les côtés du triangle O1O2O3 sont parallèles à ceux du triangle ABC, il est facile, avec un logiciel de géométrie dynamique de placer un centre O1 sur la bissectrice de l'angle en BAC, et construire les centres O2 et O3 à l'intersection des parallèles aux côtés de l'angle BAC et des deux autres bissectrices, puis de construire trois cercles tangents chacun à deux côtés du triangle.
Déplacer le point O1 de telle manière que les trois cercles soient sécants en T.
Une construction
gb dans le phorum les-mathematiques.net a montré que 1/r = 1/R + 1/R’.
Il note que :
L'homothétie de centre I et de rapport r/R transforme le cercle circonscrit à ABC, de rayon R = IA,
en le cercle circonscrit à O1O2O3 de rayon r = IO1.
Le rapport d'homothétie est r/R = IO1/IA.
Soit une autre homothétie de centre A qui transforme le cercle inscrit dans ABC en le cercle de centre O1 tangent aux côtés [AB] et [AC] ;
Cette homothétie transforme I en O1 ; H2 en H1 ;
le rayon [IH2] en le rayon [O1H1].
Le rapport d'homothétie est AO1/AI = O1H1/IH2 = r/R’.
D'où r/R’ + r/R = AO1/AI + O1I/AI = (AO1 + O1I)/AI = 1
et en divisant par r : 1/R + 1/R’ = 1/r.
Il suffit alors de tracer les parallèles aux côtés, situées à une distance r de ceux-ci, pour obtenir la solution du problème.
Figure interactive de GeoGebraTube : trois cercles égaux tangents à l'intérieur d'un triangle
Construction de Wallis
Plus ludique, nous avons fait ci-dessus pour un triangle non isocèle en A, le tracé à partir du point T, sur le segment [IO], que gb a montré comme étant l'image de O par l'homothétie de centre I et de rapport r/R.
Il suffit alors de tracer le cercle passant par le point T, tangent aux côtés [AB] et [AC]. C'est donc un problème PDD que nous ramenons à un problème PPD en construisant le point T’, symétrique de T par rapport à la bissectrice de l'angle A.
Pour cela, la construction de Wallis, d'un cercle passant par T et T’ tangent à (AB), permet de tracer le point K, intersection de la droite (TT’) avec le côté (AB), et le cercle de diamètre [TT’].
Une tangente, issue de K, coupe ce cercle en M.
Le cercle de centre K, passant par M, coupe le côté [AB] en H1, point de contact du cercle tangent cherché ;
d'où son centre O1 ;
puis les deux autres cercles.
Page no 165, créée le 25/1/2011
mise à jour le 6/8/2014