Descartes et les Mathématiques
Les vecteurs
Addition de vecteurs, multiplication d'un vecteur par un réel, prototype GéoPlan
Sommaire
En 1970, l'enseignement des vecteurs avait en France 50 ans d'avance, maintenant il a 50 ans de retard !
Définition
Définir le vecteur à partir du parallélogramme : 
= 
si ABCD est un parallélogramme.
Au collège et au lycée, on ne parle plus de classe d'équivalence de bipoints.
Quelques vecteurs
, 
, , 
, 
Repères
a) Droite : (A, 
)
b) Plan : (O, 
, 
) ; (O, , 
)
c) Espace : (O, , , 
) (O, , , 
)
1. Prototype (technique GéoPlan pour le professeur)
Un prototype est une macro, fonction au sens informatique du terme, qui une fois défini permet, comme tout article du menu « Créer », de construire un objet à partir d'autres objets.
Vecteur sur bipoint (A, B)
GéoPlan n'a pas prévu le tracé de vecteur, mais on peut, par exemple, définir le prototype « vecteur sur bipoint (A,B) » qui, à partir d'un bipoint (A, B), fabriquera la flèche représentant un vecteur.
Pour cela, à partir de deux points A et B, avec des similitudes créer deux points B1 et B2, extrémités de la flèche, et – astuce GéoPlan pour obtenir un seul objet – créer un polygone ABB1BB2B.
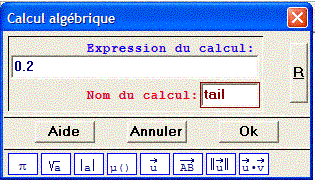
Avec l'option calcul algébrique, on crée une variable numérique tail = 0.2 qui correspond à la taille de la pointe de la flèche.
Ici 0,2 unité (modifiable en fonction de l'échelle de la figure).
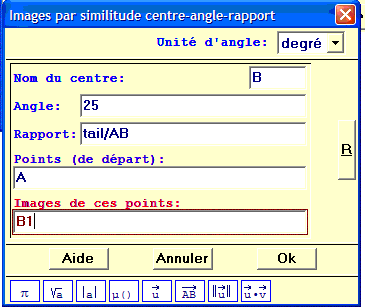
Avec une similitude, il faut ensuite construire un des points B1 de la pointe de la flèche.
> Créer
> Point
> Point image par
> Similitude (centre - angle en degré - rapport)
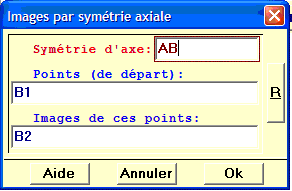
Avec une symétrie axiale, on construit ensuite l'autre point B2 de la pointe de la flèche.
Avec le menu aspect des objets, effacer (non dessiné) les noms B1 et B2.
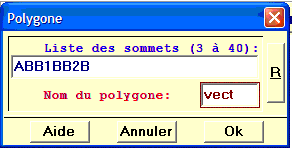
Le polygone ABB1BB2B nommé vect correspond au dessin de la flèche du vecteur.
Télécharger la figure GéoPlan def_vecteur.g2w
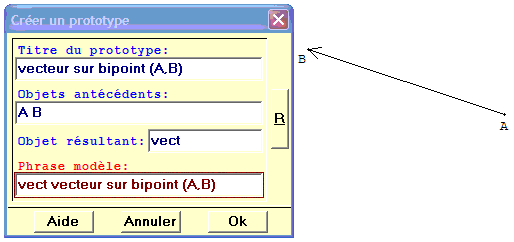
Valider dans le menu : divers > créer un prototype, ce qui servira pour faire le vecteur , mais aussi d'autres vecteurs.
On donne le titre du prototype :
vecteur sur bipoint (A,B)
L'objet polygone est créé; à partir de deux points A et B et a été appelé vect.
Dans la phrase modéle, il faut reprendre le nom vect de l'objet résultant suivi des objets antécédents.
Phrase modéle : vect vecteur sur bipoint (A,B)
La figure GéoPlan vecteur.g2w contient le prototype créé par le logiciel. L'enregistrer sous (un nouveau nom) pour pouvoir dessiner des vecteurs ou coller le texte de la macro au début d'une figure existante (les noms des points antécédents et du polygone résultant ont été modifiés pour rendre le prototype plus lisible) :
Début de [vecteur sur bipoint (A,B)] A point donné B point donné tail = 0.2 B1 image de A dans la similitude (centre B angle 25 rapport tail/AB) B2 image de B1 par la symétrie d'axe (AB) vect polygone ABB1BB2B Description de l'interface vect vecteur sur bipoint (A,B) Origine (point): Extrémité (point): Nom de la flèche: Fin de [vecteur sur bipoint (A,B)]
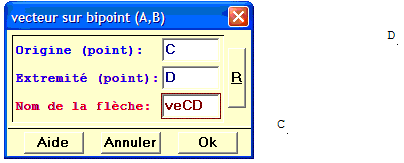
Dans le menu « Créer », on trouve alors :
> objet selon un prototype
> vecteur sur bipoint (A,B)
GéoPlan va créer la flèche avec l'instruction :
veCD vecteur sur bipoint (C,D)
Voir d'autres prototypes : marquer un angle ou marquer un angle droit
2. Addition de vecteurs
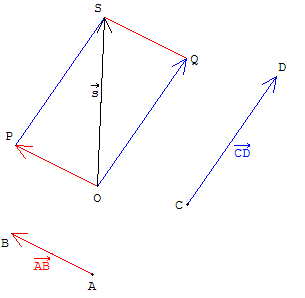
Méthode du parallélogramme OPSQ :
=
+ 
= 
+ 
= 
.
Déplacer les points A, B, C, D ou O.
Technique GéoPlan
Pour afficher les noms des vecteurs nommer u1, v1 et s1 les milieux des segments [AB], [CD] et [OS], éditer le texte de la figure puis à la fin, avant le commentaire écrire :
A la place de u1, afficher: \vec(A,B)\ A la place de v1, afficher: \vec(C,D)\ A la place de s1, afficher: \vec(s)\
Télécharger la figure GéoPlan som_vect.g2w
3. Multiplication d'un vecteur par un nombre réel
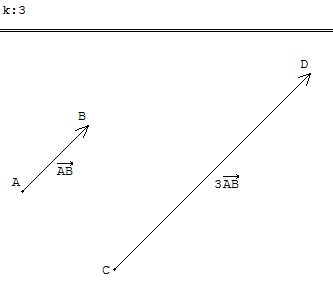
= k .
Déplacer les points A, B ou C ;
modifier k avec les flèches du clavier, touches + ou - pour modifier le pas de pilotage.
Technique GéoPlan
Pour afficher les noms des vecteurs et k ,
nommer u1 et v1 les milieux des segments [AB] et [CD] puis à la fin du texte de la figure écrire :
A la place de u1, afficher: \vec(A,B)\ A la place de v1, afficher: \val(k,2)\ \vec(A,B)\
Télécharger la figure GéoPlan mul_vect_reel.g2w
4. Combinaison linéaire de deux vecteurs
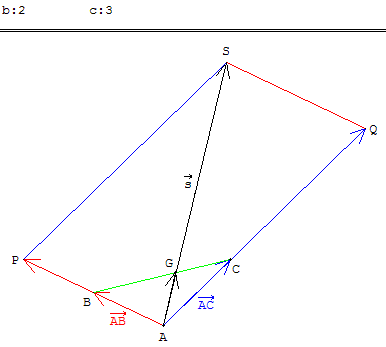
Technique du parallélogramme APSQ :
= b
+ c 
= 
+ 
= 
.
Remarque pour la 1ère S : si b + c ≠ 0, le point G, intersection des droites (AS) et (BC), est le barycentre de (B, b) et (C, c) ;
= 
(b
+ c ) = .
Avec GéoPlan, déplacer les points A, B ou C ;
modifier b ou c avec les flèches du clavier,
taper B pour modifier b,
taper C pour modifier c.
Télécharger la figure GéoPlan combin_vect.g2w
Table des matières
Faire de la géométrie dynamique
Copyright 2005 - © Patrice Debart
Page no 79, réalisée le 6/3/2005