
Journées Nationales de l'APMEP
Math en marche
Grenoble - 22 au 25 octobre 2011

Atelier APMEP,
JN de Grenoble 2011
Compte rendu
![]() pdf
pdf
Document d'accompagnement de l'atelier 49
Atelier 049 du 24 octobre
Faire de la géométrie dynamique du collège à la première
Patrice Debart, professeur retraité
Atelier TP réalisé devant 10 collègues, du collège au lycée, avec ordinateurs (personnels ?) et utilisation d'un vidéoprojecteur.
Transformer, optimiser… Utiliser GéoPlan ou GeoGebra avec des élèves qui n'ont plus l'étude des transformations au collège ni de cours de géométrie en première.
La présentation avec GeoGebra de deux exemples (un exercice élémentaire et un scénario plus sophistiqué pour le lycée) sera suivie d'un échange sur la géométrie et Internet :
• Quels sont les problèmes consistants au sens de la géométrie dynamique ?
• Quelles ressources mettre à disposition sur le net ?
• Au moment où l'institution se désintéresse de la géométrie, va-t-elle devenir une activité réservée à Internet ?
Référence
Atelier : http://www.debart.fr/APMEP/JN_Grenoble.html
Image de Sébastien Leclerc : Traité de géométrie théorique et pratique
Deux triangles isocèles
Énoncé
On considère un triangle isocèle ABC dans lequel la médiatrice du côté AC coupe le prolongement de la base BC au point D.
On joint DA que l'on prolonge d'une longueur AE = BD.
– Montrer que le triangle DAC est isocèle. Conséquences ?
– Comparer les triangles ABD et CAE.
– Que peut-on dire du triangle CDE ?
1. Euclide
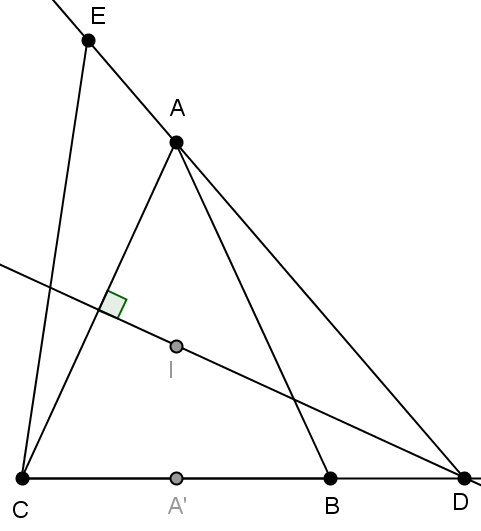
démonstration par le deuxième cas d'isométrie des triangles
Les triangles ABD et CAE sont isométriques, car :
– les côtés sont de même mesure par construction : BD = AE et AB = CA,
– les angles ABD et CAE sont égaux, car ils ont même supplémentaire α.
De l'isométrie des triangles ABD et CAE,
on déduit l'égalité des angles CDE = DEC.
Le triangle CDE est isocèle, car deux angles sont égaux.
Avec GeoGebra, noter les égalités des côtés, marquer les angles égaux α = ABC = ACB, puis α = CAD et dessiner les triangles isométriques ABD et CAE.
Lorsque l'on déplace le point A, le triangle DAC est isocèle tant que D est à l'extérieur de [BC].
Après le cas particulier du triangle équilatéral, lorsque α < 60°, le triangle DAC n'est plus isocèle.
2. Rotation
Il est facile d'identifier la rotation qui transforme le triangle ABD en CAE, en dessinant le centre I du cercle circonscrit à ABC.
Le centre de la rotation est situé sur la médiatrice de [AC] et sur la médiatrice de [BA], c'est donc le point I. L'angle de la rotation est l'angle au centre 2α du triangle ABC.
Cette rotation permet d'obtenir une construction du point E (attention au sens des angles avec GeoGebra).
Le triangle DAC est isocèle quel que soit l'angle α.
3. Symétries
Une troisième démonstration très simple du fait que CDE est isocèle :
La symétrie par rapport à la médiatrice de [BC] transforme ABD en ACD’,
la symétrie par rapport à la médiatrice de [AC] transforme ACD’ en CAE.
Référence
Deux triangles isocèles: http://www.debart.fr/APMEP/geogebra/triangle_isocele_classique.html
Carré inscrit dans un pentagone
Énoncé
Construire un carré aussi grand que possible à l'intérieur d'un pentagone régulier.
Construction
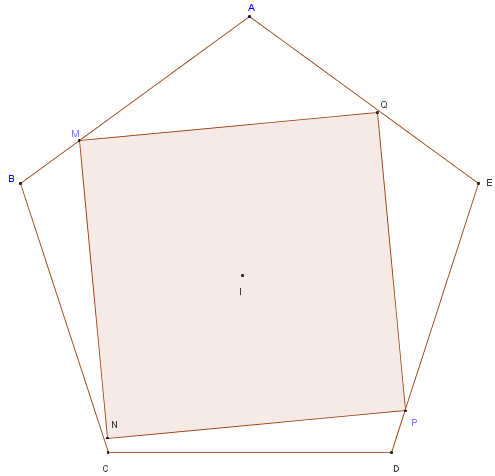
Pour construire un pentagone régulier ABCDE de côté a = 1 avec GeoGebra, créer deux points : A de coordonnées (0 ; 0,85) et B de coordonnées polaires (0,85 ; 162°) et dessiner le pentagone penta=Polygone[A, B, 5].
1. Carré ayant deux sommets consécutifs sur le pentagone
Pour un point M sur [AB] et N sur les côtés [AB] ou [BC] {N = Point[penta]}, tracer le carré MNPQ. Montre si P et Q sont strictement à l'intérieur du pentagone, on peut trouver un carré plus grand.
Un tel carré maximal a trois sommets sur le pentagone et la recherche peut se réorienter vers des carrés ayant deux sommets opposés situés sur le pentagone.
2. Carré ayant deux sommets opposés sur deux côtés consécutifs du pentagone
Soit le point M sur [AB] et P sur le côté [BC]. Le carré MNPQ n'est pas à l'intérieur du pentagone.
3. Carré ayant deux sommets opposés sur deux côtés non consécutifs du pentagone
Étudier le cas où le point M est sur [AB] et P est sur le côté [DE].
Vérifier que N ou Q sont sur le pentagone : un carré maximal a trois sommets sur le pentagone
4. Carré inscrit dans le pentagone
Si trois des sommets du carré (distincts des sommets du pentagone) sont situés sur le pentagone alors les quatre sommets y sont : le carré est inscrit dans le pentagone.
Prendre les points variables N sur [BC] et P sur [DE]. La recherche du carré est facilitée avec une figure de clôture : La perpendiculaire en P à (NP) coupe [AE] en Q, la perpendiculaire en Q à (PQ) coupe [AB] en M, reporter, en N1, la longueur NP sur la perpendiculaire en M à (MQ). Faire coïncider N et N1 ; conclure au parallélisme de (CD) et (NP).
5. Carré ayant un sommet en commun avec le pentagone
Carré AMNP à l'intérieur du pentagone.
On trace le cercle circonscrit au pentagone de centre O. Tracer [M’P’], le diamètre perpendiculaire au rayon [OA], puis les segments [AM’] et [AP’].
Trouver le carré maximal et conclure.
Référence
Carré inscrit dans un pentagone : http://www.debart.fr/APMEP/carre_ds_pentagone/pentagone_carre_classique.html
![]() « Descartes et les Mathématiques »
« Descartes et les Mathématiques »
Accueil : www.debart.fr
Page créée le 18/10/2011