Aire minimale de deux carrés dans un carré

Descartes et les Mathématiques Optimisation en classe de seconde avec GeoGebra
Sommaire Recherche de minimum Parabole avec GeoGebra		Exemples de contenu pour l'enseignement en seconde Le plus grand rectangle inscrit dans un triangle rectangle Le plus grand rectangle inscrit dans un triangle isocèle Le plus grand triangle isocèle inscrit dans un cercle
Version interactive	Avec GeoGebra : Optimisation d'aires	Statue de la Liberté	Menu optimisation
Aire minimale de deux carrés dans un carré Énoncé On considère un carré ABCD de côté 4. On place un point M, variable sur la diagonale ]AC[, et par M on trace deux parallèles aux côtés du grand carré qui le partagent en deux carrés et deux rectangles. Il s'agit de déterminer la position du point M sur le segment [AC] pour que la somme des aires des petits carrés soit minimale. Remarque : on retrouve cette figure dans les Éléments où Euclide montre que les deux rectangles ont même aire. À une ou deux affinités près, cet exercice se traite dans un rectangle ou dans un parallélogramme. On obtient toujours la même conclusion : Le minimum est atteint pour le milieu de la diagonale.
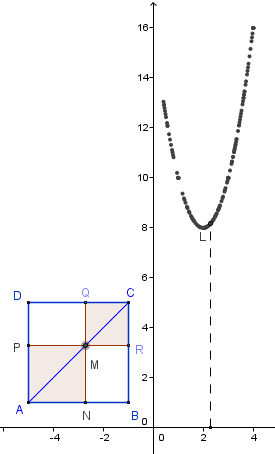
Aire minimale avec la géométrie dynamique Sur une feuille de travail GeoGebra, on affiche les axes. – On construit le carré ABCD et un point M sur la diagonale. On calcule la différence a des abscisses de M et de A. – On construit les carrés ANMP et MRCQ, GeoGebra renvoie leurs aires que l'on somme dans la variable b. – On construit enfin le point L de coordonnées (a, b) dont on active la trace. On peut dès lors faire varier le point M et conjecturer le minimum b = 8, pour a = 2.
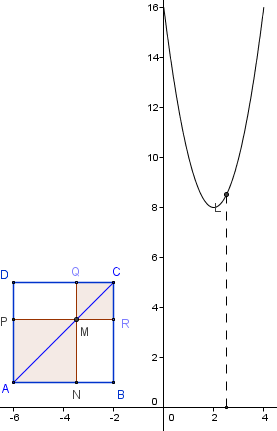
Parabole avec GeoGebra – En déplaçant M sur toute la diagonale, on observe que la trace semble être une branche de parabole. Pour effacer la trace du point L, cliquer sur « Réinitialiser la construction » ou appuyer simultanément sur les deux touches CTRL et F. – Cocher la case parabole de recherche, saisir la fonction carré f(x) = x^2, et l'«amener » sur la trace par trouve la fonction f représentant l'aire. – Cocher la case parabole solution : GeoGebra affiche alors la fonction (x - 2)² + 8, ce qui permet de répondre à la question. En effet, ce calcul de l'aire est du second degré, avec 1 pour coefficient de x². Vérifier la parabole sur trois points suffit pour valider le résultat. Le lieu des points est alors,une parabole. Figure interactive dans GeoGebraTube : aire minimale de deux carrés dans un carré
Mobile friendly		Page n^o 187, créée le 2/11/2011 mise à jour le 18/11/2013