Descartes et les Mathématiques
L'axe orthique, droite de 24 points
Polaires de l'orthocentre par rapport au cercle circonscrit et au cercle d'Euler
Mobile friendly ; sur ordinateur, version desktop
1. Données
2. Droite de 12 points
3. Indications pour une démonstration par homothétie
4. Détermination géométrique du centre du cercle d'Euler
5. Indications pour une démonstration par inversion
Inversion échangeant le cercle circonscrit et le cercle d'Euler
1. Données
Soit ABC un triangle et cercle (c) son cercle circonscrit, de centre O.
On désigne par H son orthocentre ;
AA1, BB1, CC1 : les trois hauteurs, A1, B1, C1 les pieds des hauteurs, formant le triangle orthique, inscrit dans le cercle d'Euler (c’) du triangle ABC ;
Ω, milieu de [OH], est le centre du cercle d'Euler ;
A", B", C" : les milieux des segments [AH], [BH], [CH], situés sur le cercle d'Euler ;
A2, B2, C2 : les intersections des trois hauteurs avec le cercle circonscrit (c), symétriques de l'orthocentre ;
P, Q, R : les intersections des droites (BC, B1C1), (CA, C1A1), (AB, A1B1) ;
P’, Q’, R’ : les intersections de (B"C", B2C2), (C"A", C2A2), (A"B", A2B2) ;
I, J, K : les intersections de (B1C", BC2), (C1A", CA2), (A1B", AB2) ;
I’, J’, K’ : les intersections de (C1B", CB2), (A1C", AC2), (B1A", BA2);
P1, Q1, R1 : les intersections de (B"C", B1C1), (C"A", C1A1), (A"B", A1B1) ;
I1, J1, K1 : les intersections de (B"C1, C"B1), (A"C1, C"A1), (B"A1, A"B1) ;
P2, Q2, R2 : les intersections de (BC, B2C2), (CA, C2A2), (AB, A2B2) ;
I2, J2, K2 : les intersections de (BC2, CB2), (CA2, AC2), (AB2, BA2).
2. Douze points remarquables sur l'axe orthique
- Les points P, Q, R ; intersection des côtés du triangle et de ceux du triangle orthique A1B1C1, sont alignés sur un même droite Δ, axe orthique du triangle, axe radical des deux cercles (c) et (c’),
Les neuf autres points : P’, Q’, R’, I, J, K, I’, J’, K’ appartiennent à cet axe. Cet axe Δ contient donc douze points remarquables ; - Les six points P1, Q1, R1, I1, J1, K1 appartiennent à une droite D1, polaire de H par apport au cercle d'Euler ;
- Les six points P2, Q2, R2, I2, J2, K2 appartiennent à une droite D2, polaire de H par apport au cercle circonscrit ;
- L'axe orthique Δ est perpendiculaire à la droite d'Euler (l'axe radical des deux cercles est perpendiculaire à la ligne des centres OΩ) ;
- Les droites D1, D2 et Δ sont parallèles et l'axe Δ est équidistant de D1 et de D2 ;
- Par l'homothétie de centre H, de rapport 2, D2 est l'image de D1, les points P1, Q1, R1, I1, J1, K1 ont respectivement pour images P2, Q2, R2, I2, J2, K2.
Polaires de H par rapport aux cercles d'Euler et circonscrit
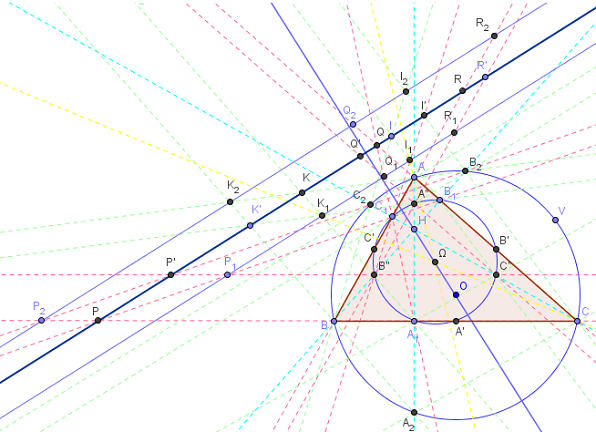
Les points J et J’sont à l'extérieur de cette figure
En 1990, date de ces trouvailles, Michel Saad avait aurait fait une démonstration par une méthode analytique basée sur les équations de cercles et de droites (niveau 1ère S) et tracé cette figure à la main.
Maintenant, avec le logiciel « GeoGebra », il est possible de vérifier ces propriétés en quelques minutes, est-ce une preuve ?
Figure dans GeoGebraTube : douze points sur l'axe orthique
3. Homothétie
Il est possible de trouver des démonstrations :
• en géométrie synthétique avec l'homothétie et la puissance d'un point par rapport à un cercle ;
• en terminale S avec les nombres complexes ou avec la méthode du barycentre ;
• après le bac, comme ci-dessous, avec une transformation du plan comme l'inversion.
Indications pour une démonstration par l'homothétie
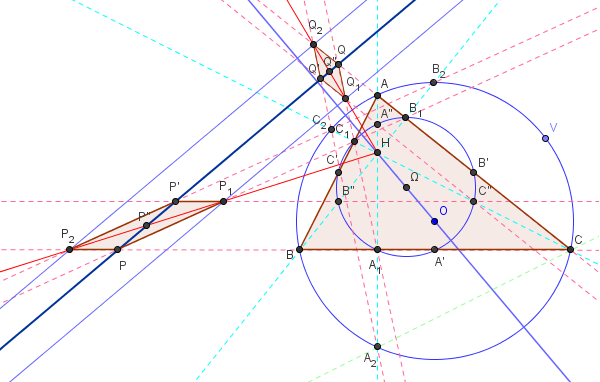
Télécharger la figure GeoGebra homo_droite_24_points.ggb
Par définition, avec l'homothétie de centre H, de rapport 2, le triangle A"B"C" a pour image ABC et le triangle orthique A1B1C1 a pour image A2B2C2.
Les intersections des divers côtés parallèles, homologues par l'homothétie, permettent de montrer l'alignement de H avec les points homologues P1P2…
On obtient six parallélogrammes PP1P’P2… chaque parallélogramme ayant l'axe orthique Δ comme diagonale, l'autre diagonale passant par le centre H.
Six autres points remarquables
La droite (HP2), diagonale du parallélogramme PP1P’P2, coupe Δ au « centre remarquable » P’’, milieu des diagonales [P1P2] et [PP’].
Les six milieux de ces diagonales [P1P2], [Q1Q2], [R1R2], [I1I2], [J1J2], [Q1Q2] et [K1K2] sont autant de points remarquables situés sur l'axe orthique Δ.
Ces milieux sont donc les images des six points P1, Q1, R1, I1, J1, K1 de la droite D1, par l'homothétie de centre H et de rapport 
, ces images sont bien situées sur l'axe Δ.
4. Détermination géométrique du centre du cercle d'Euler
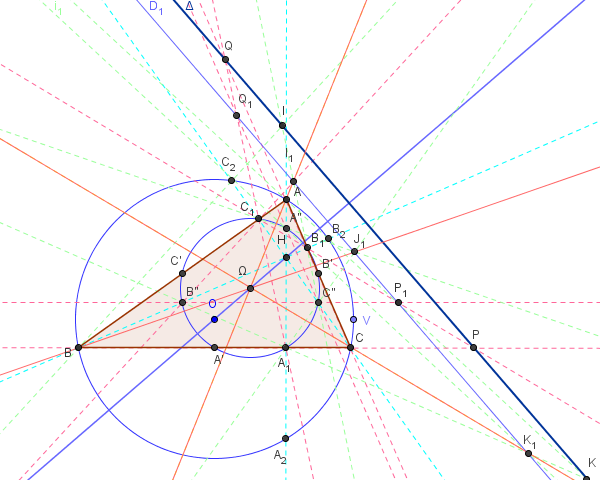
- Les droites (AI1), (BJ1), (CK1) sont concourantes en Ω, centre du cercle d'Euler (c’) du triangle ABC.
Ω centre du cercle d'Euler, point X(5) de ETC.
en : nine-point center - center of the nine-point circle
Figure dans GeoGebraTube : détermination du centre du cercle d'Euler
5. Indications pour une démonstration par inversion
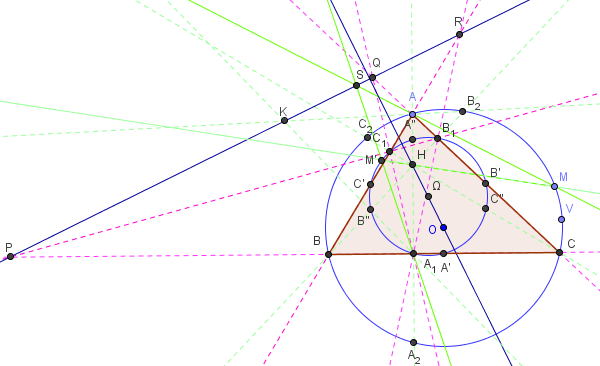
Télécharger la figure GeoGebra droite_24_points_inversion.ggb
Une inversion de pôle H transforme le cercle circonscrit (c) en (c’), cercle d'Euler.
Dans cette inversion, le point A a pour image A1. Si M est un point de (c), la droite (MH) coupe (c’) et en choisissant le point d'intersection situé à l'extérieur du segment [MH], on trouve le point M’ image de M par l'inversion.
La droite (AM) et, son antihomologue, la droite (A1M’), se coupent en un point S, situé sur l'axe radical des deux cercles.
Cette remarque, avec la figure ci-dessous, permet de retrouver 4 points remarquables de l'axe Δ.
Où l'on retrouve l'axe orthique Δ, contenant les deux points Q et R, ainsi que les points K et J, comme axe orthique
En plaçant M en B, puis en C, on montre que l'axe Δ, contenant les points Q et R, est l'axe orthique.
Le troisième point P se trouve à partir de (BM) et B1 (ou C et C1).
En plaçant M en B2, puis en C2, on trouve que K et J sont sur l'axe radical.
Technique GeoGebra : déplacer le point M sur le cercle (c).
D'autres points sur l'axe orthique Δ
Cinq autres points remarquables se retrouvent par permutation circulaire : à la place de A, mettre B avec (BM) et, son antihomologue, la droite (B1M’),
puis mettre C avec (CM) et, son antihomologue, la droite (C1M’).
Par ailleurs, le point P’ est l'intersection de (B2C2) et de son antihomlogue (B"C") ; de même pour Q’ et R’.
L'inversion a donc permis de démontrer que les 12 premiers points remarquables étaient sur l'axe orthique.
Intersections de tangentes
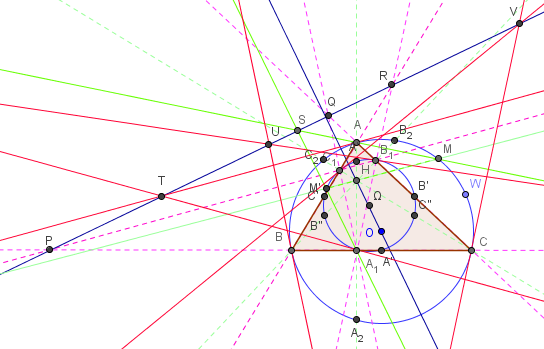
Télécharger la figure GeoGebra droite_24_points_tangente.ggb
Par position limite, les tangentes en M au cercle (c) et en, son homologue, M’ au cercle (c’), se coupent en S sur l'axe radical.
Technique GeoGebra : déplacer le point M sur le cercle (c).
Remarque : S est l'intersection de la médiatrice de [MM’] avec l'axe Δ. En effet, comme S est sur l'axe radical, MS2, la puissance de S par rapport à (c) est égale à M’S2, puissance de S par rapport à (c’). MS = M’S, le triangle MM’S est isocèle, et on retrouve une propriété générale de l'inversion de deux courbes : les tangentes en deux points homologues M et M’ sont symétriques par rapport à la médiatrice de [MM’].
Trois paires de tangentes
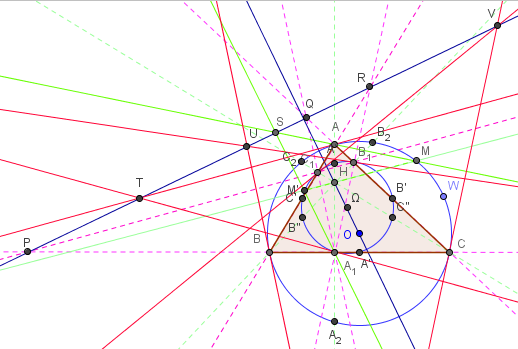
Par position limite, dans la situation 5 de la droite (AM), lorsque M tend vers A, on trouve les tangentes en A au cercle (c) et en A1 au cercle (c’) qui se coupent sur l'axe radical en T.
Par permutation circulaire on trouve le point U, intersection des tangentes en B au cercle (c) et en B1 au cercle (c’),
puis le point V, intersection des tangentes en C au cercle (c) et en C1 au cercle (c’).
Les points T, U, V sont trois autres « points remarquables » sur l'axe orthique Δ.
Télécharger la figure GeoGebra droite_24_points_tangente_1.ggb
Trois autres paires de tangentes : 24 points sur l'axe orthique
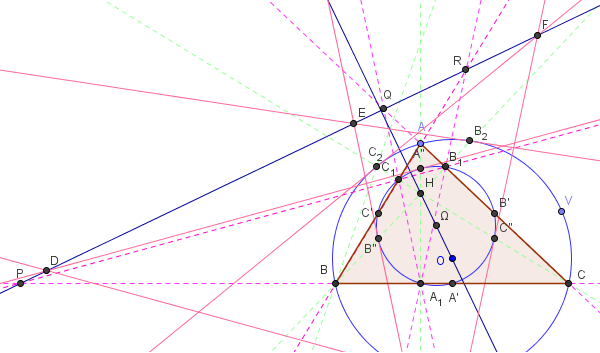
Télécharger la figure GeoGebra droite_24_points_tangente_2.ggb
Les points D, E et F sont trois autres points, soit 24 « points remarquables » sur Δ.
Ni droite des 12 points, ni droite des 24 points, il est préférable de laisser à Δ son nom d'«axe orthique ».
Glossaire
Axe orthique
L'axe orthique d'un triangle est l'axe radical du cercle circonscrit et du cercle d'Euler de ce triangle.
Il contient les trois points d'intersection des côtés du triangle et de ceux du triangle orthique.
Il est perpendiculaire à la droite d'Euler.
Axe radical
L'axe radical de deux cercles, de centres distincts, est l'ensemble des points ayant même puissance par rapport à ces deux cercles. C'est une droite perpendiculaire à la ligne des centres. Si les cercles sont sécants, l'axe radical est la droite joignant les points d'intersection.
Les tangentes menées aux deux cercles, à partir d'un point de l'axe radical (extérieur aux deux cercles), ont la même longueur.
Voir : géométrie du cercle
Pour cette « droite de 24 points », je me contente des démonstrations par « GeoGebra », qui me semble suffisamment sûres !
Bibliographie
Juillet 2009 : peu de références et de démonstrations sur le net.
On peut retrouver l'axe orthique L3 et les points X(230), X(232) et X(523) dans ETC
Septembre 2012 : diophante.fr, site de problèmes mathématiques !
le site diophante.fr revient sur ce très bel alignement de 24 points.
En 2009 dans l'article ci-dessus, Patrice Debart a montré que les 12 points remarquables appartiennent à l'axe orthique
et a identifié 12 autres points, soit une « droite des 24 points ».
Pour diophante.fr, Dominique Roux et Jean Nicot proposent deux solutions.
Page no 145, créée le 18/6/2009
adaptée aux mobiles le29/11/2016