Descartes et les Mathématiques
Ellipse d'Euler avec GeoGebra
Sommaire
1. O et H foyers d'une conique tritangente au triangle
2. Détermination géométrique du centre du cercle d'Euler
Avec GeoGebra
Avec GéoPlan
Coniques à centre : ellipse, hyperbole
1. O et H foyers d'une conique tritangente au triangle
L'ellipse d'Euler est une conique, tangente aux trois côtés d'un triangle, ayant pour foyers l'orthocentre et le centre du cercle circonscrit.
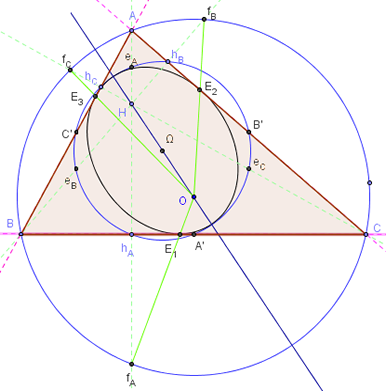
Soit ABC un triangle acutangle, ni rectangle, ni équilatéral.
Considérons la conique de foyer H et de cercle directeur le cercle circonscrit au triangle ABC, de centre O. Puisque les hauteurs (AH), (BH) et (CH) coupent ce cercle aux points fA, fB et fC symétriques de H respectivement par rapport aux côtés (BC), (AC) et (AB), ces trois points permettent de construire les points de la conique en lesquels les côtés du triangle seront tangents à la conique.
On construit ainsi E1 intersection de (OfA) et (BC), de même E2 puis E3. Puisque Ω, le centre du cercle d'Euler, est le milieu entre les deux foyers O et H, c'est le centre de la conique, on peut donc construire trois autres points de la conique E’1, E’2 et E’3, symétriques de E1, E2 et E3 par rapport à Ω, et ainsi construire la conique.
IL est aussi possible de construire des symétriques par rapport à l'axe (OH).
L'ellipse est donc tritangente en E1, E2 et E3 aux côtés du triangle.
Elle a pour cercle principal, l'homothétique du cercle circonscrit par l'homothétie de centre H et de rapport 
, soit, le cercle d'Euler.
Remarque : avec GeoGebra, la construction d'une conique à centre est faite en désignant les deux foyers et le point E1.
Il est aussi possible d'utiliser cinq points de l'ellipse : les points de contact E1, E2, E3, et par exemple E’1, E’2 , deux symétriques de E1, E2 par rapport à Ω.
Figure interactive dans GeoGebraTube : ellipse d'Euler
2. Détermination géométrique du centre du cercle d'Euler
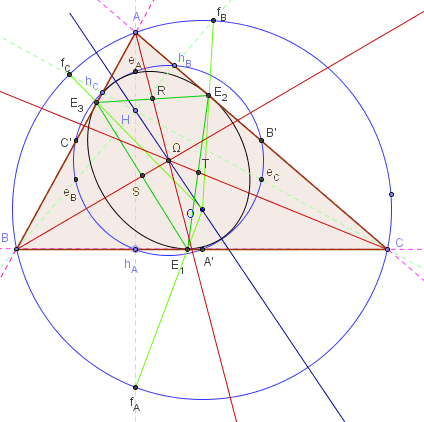
On rappelle que E1, E2 et E3 les points où (OfA), (OfB) et (OfC) coupent les côtés (BC), (CA), (AB) (ce sont les points de contact des côtés de ABC avec la « conique d'Euler »),
puis R, S, T les milieux de (E2E3), (E3E1), (E1E2).
Alors les droites (AR), (BS), (CT) concourent en Ω.
Dix droites passant par le centre
Sur cette figure, avec Ω milieu de [OH], on a quatre droites passant par Ω.
On peut trouver trois autres médiatrices du triangle médian concourantes au centre du cercle d'Euler.
On peut trouver encore trois autres médiatrices du triangle orthique concourantes en Ω.
Voir aussi : 24 points sur l'axe orthique
Mobile friendly
Page no 147, créée le 18/7/2009
mise à jour le 18/11/2013