Descartes et les Mathématiques
Hyperbole avec GeoGebra
Homothétie transformant deux hyperboles
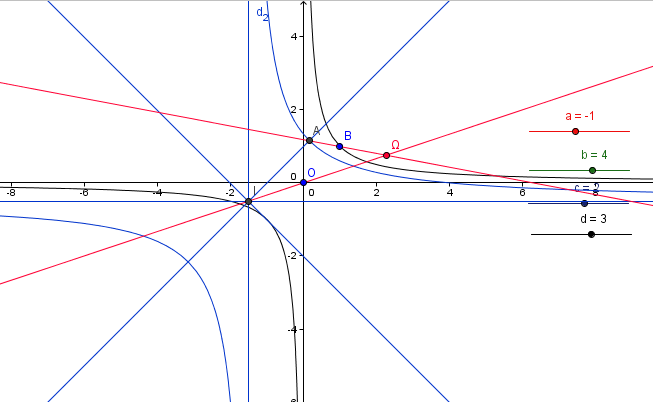
On utilise le logiciel GeoGebra.
• On crée quatre curseurs a, b, c et d prenant tous des valeurs entre - 10 et 10.
• On crée les fonctions définies par f(x) = (ax + b)/(cx + d) et h(x) = 1/x.
• Modifier la valeur des curseurs a, b, c et d.
H1 est une hyperbole de centre I(-d/c, a/c), H2 a pour centre O.
L'image par l'homothétie d'un point A de l'hyperbole H1 est un point B situé sur l'hyperbole H2.
Le centre Ω de l'homothétie est à l'intersection des droites (OI) et (AB).
Figure interactive dans GeoGebraTube : hyperboles homothétiques
Mobile friendly
La géométrie dynamique
…avec GeoGebra
Trisection : hyperbole de Chasles
Capes, page no 11, créée le 20/1/2009
mise à jour le 28/11/2013