Descartes et les Mathématiques
Les Coniques du problème de Pappus
Figures interactives avec GeoGebra
1. Le problème de Pappus « à quatre droites »
2. Solution du problème de Pappus « à quatre droites »
3. Cercle solution du problème de Pappus
4. Parabole
5. Conique de Pappus passant par un point donné
Le problème de Pappus dans la Géométrie (version classique)
Problème de Pappus à quatre droites
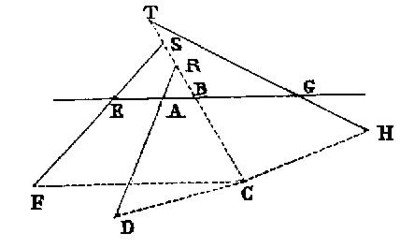
1. Le problème de Pappus « à quatre droites »
Le problème de Pappus « à quatre droites » est la recherche du lieu géométrique d'un point C tel que le produit des distances de C à deux d'entre elles soit égal au produit des distances de C aux deux autres droites.
Descartes utilise des rapports de similitude plutôt que des distances et cherche le lieu du point C dont les segments menés de ce point à chacune des droites suivant des directions données ont des produits égaux.
Étant donné les quatre droites (AB), (EF), (AD) et (GH), le problème de Pappus, est de trouver le lieu géométrique des points C dont les segments (en pointillés sur la figure ci-dessus) menés de ce point C à chacune des droites suivant des directions données ont des produits égaux.
Le lieu de Pappus est alors l'ensemble des points C tel que CB × CF = CD × CH.
2. Solution du problème de Pappus « à quatre droites »
Dans la page des figures de Pappus, nous avons fait, avec GéoPlan, les figures des calculs de Descartes.
Ici, avec GeoGebra nous ferons des projections orthogonales et nous utilisons un repère orthonormé, d'origine A, où nous respectons les notations modernes.
Descartes exprime les longueurs des segments en fonction de deux inconnues x et y et en liaison avec la notion moderne de « distance d'un point à une droite donnée par son équation ».
La droite (AB) est choisie comme axe des abscisses, AB comme abscisse et CB comme ordonnée,
puis les trois droites (EF), (AD) et (GH), données de position par rapport à la première, ont pour équations ax + by + c = 0, dx + ey = 0 et fx + gy + h = 0 (avec a2 + b2 = 1 ; d2 + e2 = 1 ; f2 + g2 = 1).
Pour un point C(x, y), nous utilisons les mesures algébriques des projections orthogonales :
x = 
, y = 
, 
= ax + by + c, 
= dx + ey et 
= fx + gy + h.
Le lieu des points C tel que CB × CF = CD × CH est celui des points tel que × = ± × .
D'où deux équations du second degré y × (ax + by + c) = ± (dx + ey) × (fx + gy + h) qui sont celles des deux coniques du lieu.
Ces coniques passent par quatre points situés aux intersections des droites : les points A et G, et les points P et Q situés sur la droite (ES).
Une des deux courbes a été oubliée dans les calculs de Descartes.
Cas général
Figure interactive dans GeoGebraTube : problème de Pappus
3. Cercle solution du problème à 4 droites
Cas où le coefficient de xy, dans l'équation de la conique, est nul.
Figure interactive dans GeoGebraTube : cercle solution du problème de Pappus
Voir aussi les calculs de Descartes dans les figures de Pappus avec GéoPlan
4. Parabole solution du problème à quatre droites
Cas où le coefficient de y2, dans l'équation de la conique, est nul.
Figure interactive dans GeoGebraTube : parabole du problème de Pappus
Voir aussi les calculs de Descartes dans les figures de Pappus avec GéoPlan
5. Conique de Pappus passant par un point donné
Par tout point C du plan, il est possible de construire une conique (ou deux droites) passant par C, solution du problème de Pappus.
Déplacer le point C avec la souris.
Remarque :
Pour tout point C on a le rapport
λ = (CB × CF) /(CD ×CH).
La conique de Pappus passant par C est le lieu des points M tels que :
(MB × MF) /(MD × MH) = λ (où B, F, D et H sont les projections de M).
En inversant le sens, une deuxième conique complète le lieu des points M tels que :
(MB × MF) /(MD × MH) = λ.
Figure interactive dans GeoGebraTube : conique de Pappus passant par un point
La Géométrie
Livre premier
Théorème de Pappus : plan projectif
Petit théorème de Pappus
Parallélogramme de Pappus : homothétie
Démonstration de Pappus du théorème de Pythagore
Glossaire
Publimath : problème de Pappus
La Géométrie - Livre second – texte et notes pour mobiles
De la nature des lignes courbes
Livre troisième – texte et notes pour mobiles
Page no 23, réalisée le 28/10/2010