Descartes et les Mathématiques

Descartes et le problème de Pappus

Figure interactive avec GeoGebra

Notes sur Pappus version classique	Œuvre mathématique de René Descartes	La Géométrie Livre premier	Les coniques du problème de Pappus à 4 droites avec GeoGebra – Figures classiques
Le problème de Pappus (figures classiques) Descartes et le problème de Pappus 1. Note sur le Problème de Pappus 2. Observations 3. Solution du problème de Pappus à quatre droites avec GeoGebra 4. Lieu à cinq droites dans la Géométrie de Descartes			Problème de Pappus à quatre droites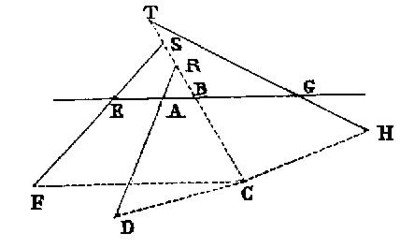

Le problème de Pappus

Le problème de Pappus « à quatre droites » est de construire le lieu géométrique d'un point C tel que le produit des distances de C à deux d'entre elles soit égal au produit des distances de C aux deux autres droites ;
tel que le produit des distances de C à deux d'entre elles soit égal au carré du produit des distances de C à la troisième droite pour le problème avec trois droites.

Descartes utilise des rapports de similitude plutôt que des distances et cherche le lieu du point C dont les segments menés de ce point à chacune des droites suivant des directions données ont des produits égaux.

1. Note sur le Problème de Pappus

Traduction du texte grec de Pappus, d'après l'édition de Fr. Hultsch
(Pappi Alexandrini Collectionis quœ supersunt, vol. II, Berlin, Weidmann, 1877, pp. 676-680).

Nous donnons tout d'abord le passage, visé dans ce texte, du préambule du livre I des Coniques d'Apollonius :

« Le livre III contient nombre de théorèmes remarquables, qui sont utiles pour la synthèse des lieux plans et la détermination des conditions de possibilité des problèmes.
La plupart de ces théorèmes et les plus beaux sont nouveaux ; leur découverte nous a fait reconnaître qu'Euclide n'a pas effectué la synthèse du lieu à 3 et 4 lignes, mais seulement celle d'une partie de ce lieu prise au hasard, et qu'il ne s'en est même pas heureusement tiré ; c'est que, sans nos découvertes, il n'était pas possible de faire la synthèse complète. »

Pappus : « Mais ce lieu à 3 et 4 lignes, dont Apollonius dit, à propos de son livre III, qu'Euclide ne l'a pas complètement traité, lui-même, pas plus qu'aucun autre, n'aurait pu l'achever, ni même rien ajouter à ce qu'Euclide en a écrit, du moins en s'en tenant exclusivement aux Éléments des Coniques déjà démontrés au temps d'Euclide… »

« Voici quel est ce lieu à 3 et 4 lignes, à propos duquel Apollonius se décerne de grands éloges pour ses additions et dont il aurait dû savoir gré au premier qui en a écrit. Si, trois droites étant données de position, on mène d'un même point, sur ces trois droites, trois autres sous des angles donnés, et qu'on donne le rapport du rectangle compris sous deux des menées au carré de la troisième, le point se trouvera sur un lieu solide donné de position, c'est-à-dire sur l'une des trois coniques.

« Si c'est sur quatre droites données de position que l'on mène des droites sous des angles donnés, et qu'on donne le rapport du rectangle de deux des menées à celui des deux autres, le point se trouvera de même sur une section conique donnée de position. D'autre part, si les droites sont seulement au nombre de deux, il est établi que le lieu est plan ; mais, s'il y a plus de quatre droites, le lieu du point n'est plus de ceux qui soient connus ; il est de ceux qu'on appelle simplement lignes (sans en savoir davantage sur leur nature ou leurs propriétés), et on n'a fait la synthèse d'aucune de ces lignes, ni montré qu'elle servît pour ces lieux, pas même pour celle qui semblerait la première et la plus indiquée. »

Voici comment on propose ces lieux. (Titre du traducteur)

« Si d'un point on mène à cinq droites données de position d'autres droites sous des angles donnés, et qu'on donne le rapport entre le parallélépipède rectangle compris sous trois des menées et le parallélépipède rectangle compris sous les deux autres et sous une donnée, le point se trouvera sur une ligne donnée de position. »

« Si les droites données sont au nombre de six, et que l'on donne le rapport du solide compris sous trois des menées au solide compris sous les trois autres, le point se trouvera de même sur une ligne donnée de position. »

« S'il y a plus de six droites, on ne peut plus dire que l'on donne le rapport entre quelque objet compris sous quatre droites et le même compris sous les autres, puis qu'il n'y a rien qui soit compris sous plus de trois dimensions. Cependant, peu de temps avant nous, on s'est accordé la liberté de parler ainsi, sans rien désigner pourtant qui soit aucunement intelligible, en disant le compris sous telles droites par rapport au carré de telle droite ou au compris sous telles autres. Il était cependant aisé, au moyen des rapports composés, d'énoncer et de prouver en général les propositions précitées et celles qui suivent. »

« Voici comment :

Si d'un point on mène à des droites données de position d'autres droites sous des angles donnés et que l'on donne le rapport composé de celui de l'une des menées à une autre, de celui des menées d'un second couple, de celui des menées d'un troisième, enfin de celui de la dernière à une donnée, s'il y a sept droites en tout, ou bien de celui des deux dernières, s'il y en a huit, le point se trouvera sur une ligne donnée de position. »

« On pourra dire de même, quel que soit le nombre des droites, pair ou impair. Mais, comme je l'ai dit, pour aucun de ces lieux qui suivent celui à 4 droites, il n'y a eu une synthèse faite qui permette de connaître la ligne. »

2. Observations

Nous avons déjà, dans la correspondance, discuté le passage particulièrement obscur du texte de Pappus, et nous en avons donné une traduction un peu différente de celle qui précède, pour laquelle nous avons suivi la leçon des manuscrits.

Nous ajouterons ici quelques autres remarques, d'abord sur le passage de Pappus, puis sur la solution de Descartes.

I. La façon dont les anciens traitaient le lieu à trois et quatre droites a

été magistralement élucidée dans le remarquable ouvrage de M. Zeuthen, de Copenhague, ouvrage traduit en allemand par M. von Fischer-Benzon, sous le titre : Die Lehe von den Kegelschnitten in Altertum (Copenhague, Höst, 1886). Nous relèverons donc seulement, ici, ce qui, dans le langage d'Apollonius et de Pappus, pouvait induire en erreur, au XVII^e siècle, sur l'histoire réelle de ce problème.

Il a dû être posé et résolu, par les procédés d'analyse géométrique des anciens, dans un ouvrage un peu antérieur à Euclide, les cinq Livres des Lieux Solides d'Aristée (lesquels contenaient d'ailleurs certainement les éléments de nombre de théories qui font défaut dans les Coniques d'Apollonius, et que, par suite, on a cru à tort ignorées de lui, comme les propriétés du foyer de la parabole, des directrices des coniques, etc.).

La synthèse, dont la marche était tout indiquée par l'analyse, n'offrait d'intérêt que comme exercice ou application à des données particulières ; mais il importait de réunir et d'établir les divers théorèmes nécessaires, soit pour la faciliter, soit pour la rendre complète. Ce fut le but (et non pas la synthèse elle-même) que paraît s'être proposé Euclide dans une partie de ses quatre Livres des Coniques, ouvrage qui n'était déjà plus étudié au temps de Pappus ; Euclide semble s'y être borné à réunir les travaux synthétiques des géomètres plus anciens, et cela, pour faciliter en particulier l'étude des Lieux Solides d'Aristée. Apollonius accomplit, dans son troisième Livre, la théorie laissée imparfaite (un des grands progrès qu'il réalisa fut, en particulier, la considération simultanée des deux hyperboles opposées, ou, comme nous le disons, des deux branches d'une même hyperbole) ; mais ce Livre ne pouvait être utilisé, pour le lieu à trois ou quatre droites, que si l'on connaissait déjà la solution analytique, qui, seule, pouvait mettre en lumière la véritable portée des théorèmes d'Apollonius et la façon de les appliquer.

Au commencement du XVII^e siècle, les géomètres, n'ayant plus l'ouvrage d'Aristée, pas plus que les Coniques d'Euclide, ne disposant que des quatre premiers Livres d'Apollonius et des indications très insuffisantes de Pappus, avaient donc, pour résoudre la question du lieu à trois et quatre droites, à retrouver l'analyse ancienne, dont ils ignoraient les procédés, ou à essayer une divination réellement difficile.

Aussi Descartes ne pouvait guère mieux choisir que ce lieu pour illustrer, par un exemple frappant, l'emploi de la méthode analytique nouvelle qu'il avait conçue pour faciliter l'application du calcul algébrique à la géométrie.

Le problème avait été proposé par Golius à Mydorge, au moins dès 1630 (Correspondance, tome I, p. 256, 1. 18), et à Descartes en 1631 (Ibid., p. 232-235). Dès avant la publication de sa Géométrie, Descartes l'indique à Mersenne, en t632 et 1 634, comme un problème à poser à Roberval (Ibid., p. 256 et 288). Avant 1637, Fermat (Œuvres de F., II, p. 105, 1. 2) l'avait résolu à la façon des anciens ; sa solution, très élégante, pour le lieu à trois droites, se trouvé seule conservée. Roberval ne parait s'en être occupé que plus tard, mais le 4 août 1640 (Ibid., p. 201, 8), il écrit à Fermat : « Depuis cette invention (celle de sa méthode des tangentes), je me suis appliqué aux lieux solides ad tres et quatuor lineas, lesquels j'ai entièrement restitués, quoique, pour n'y rien oublier, il ne faille guère moins de discours qu'aux six premiers Livres des Éléments. » Il avait donc dû faire la synthèse complète.

2. Le problème général, tel que l'énonce Pappus pour un nombre quelconque de droites, peut aisément se poser comme suit. Soient :

A₁ = 0, A₂ = 0, … A_n = 0,
B₁ = 0, B₂ = 0, … B_n = 0,

(Paul Tannery note A = 0 l'équation d'une droite ax + by + c = 0)

les équations de 2n droites en coordonnées rectangulaires ou obliques, λ un coefficient arbitraire, l'équation du lieu à 2n droites sera :

A₁ A₂ … A_n-1 A_n ± λ B₁ B₂ … B_n-1 B_n = 0,

tandis que celle du lieu à 2n – 1 droites serait :

A₁ A₂ … A_n-1 A_n ± λ B₁ B₂ … B_n-1 = 0.

Lieu de Pappus « à quatre droites » (AB), (EF), (AD) et (GH).

En liaison avec la notion moderne de « distance d'un point à une droite donnée par son équation », dans un repère d'axe (AB), où les trois autres droites (EF), (AD) et (GH) ont pour équations
ax + by + c = 0, dx + ey = 0 et fx + gy + h = 0 (avec a² + b² = 1 ; d² + e² = 1 ; f² + g² = 1),
on a x = , y = , = ax + by + c, = dx + ey et = fx + gy + h (avec a² + b² = 1 ; d² + e² = 1 ; f² + g² = 1).

Un lieu de Pappus « à quatre droites » est l'ensemble des points C tel que CB × CF = CD × CH.

Cette relation donne deux équations du second degré y × (ax + by + c) = ± (dx + ey) × (fx + gy + h) qui sont celles de deux coniques.

Paul Tannery note ces équations sous la forme A₁ A₂ ± λ B₁ B₂ = 0.

Dans les deux cas, l'équation est du degré n, mais, à cause du double signe λ, elle représente l'ensemble de deux courbes de ce même degré, circonstance que n'a pas relevée l'auteur de la Géométrie.

Il est à remarquer que la définition de Pappus pour le lieu en général, quand le nombre des droites est impair, ne concorde pas avec sa définition particulière pour le lieu à trois droites, qui revient à l'équation :

A₁ A₂ ± λ B² = 0.

Enfin, c'est par suite d'une heureuse erreur, puisqu'elle lui a fait aborder au moins deux cas simples du lieu à cinq lignes, que Descartes a interprété la traduction de Commandin comme si les anciens avaient traité l'un de ces cas. Quoique le texte de Pappus reste douteux, il a certainement voulu dire tout le contraire.

3. Dans sa solution générale, Descartes reconnaît nettement la nature algébrique de la courbe et le degré de l'équation ; seulement, de même qu'il classe les problèmes d'après le degré de la courbe à employer pour les résoudre avec un cercle et non avec une ligne droite, il comprend sous un même genre, d'ordre n, les courbes de degré 2n et 2n – 1. Cette nomenclature amène quelques ambiguïtés.

D'autre part, il affirme que toute courbe du genre n (degré 2n) peut être lieu pour 4n droites. Ceci est vrai pour n = 1 ; il suffit de remarquer, pour les courbes du second degré, que, le lieu passant, en général, par chacune des intersections d'une droite A avec une droite B, on a ici quatre points et que le coefficient λ donne la cinquième condition pour déterminer la conique. La proposition est encore vraie pour n = 2 (lieu à huit droites). Mais, pour les valeurs supérieures de n, le nombre des conditions nécessaires pour déterminer la courbe générale du degré 2n, dépasse celui des conditions du problème. Il n'y a donc en général, si n > 2, que certaines espèces de courbes du degré 2n qui jouissent de la propriété que leur équation puisse se mettre sous la forme de l'équation du lieu à 4 n droites.

4. Descartes explique très clairement sa solution pour le premier cas simple du lieu à cinq lignes qu'il a traité ; quant au second, ce qu'il dit est d'une obscurité probablement volontaire, et même inexact, si on le prend à la lettre. Car, supposant le lieu rapporté à un diamètre (soit l'axe des x) et à l'axe conjugué passant par le sommet (l'axe des y), il dit que les ordonnées y sont égales à celles d'une section conique, dont les abscisses z formeraient, avec les abscisses correspondantes x du lieu, un produit constant, soit m². C'est-à-dire que l'on aurait :

y² = 2 pz – et zx = m².

Mais il est clair qu'à moins de supposer nul le terme en z², l'équation en x et y sera alors du quatrième degré et non du troisième, comme elle doit être pour un lieu à cinq lignes ; que, d'autre part, si la conique est simplement une parabole y² = 2 pz, l'équation du lieu prendra la forme xy² = k³ qu'on ne voit pas le moyen de mettre sous celle qui correspond au cas examiné par Descartes.

Il a dû supposer les quatre droites parallèles symétriques par rapport à l'axe des x, et prendre la droite les traversant comme axe des y ; les équations des cinq droites sont alors :

y – a = 0, y + a = 0, y – b = 0, y + b = 0, x = 0,

et celle du lieu :

x (y² – b²) = m (y² – a²).

En posant ma² = b²c, c – m = n, x = c + x’, on ramène cette équation à la forme y² = .

En posant maintenant x’ + n = on a y² = (n – z). On arrive bien ainsi à l'équation d'une parabole ; seulement l'abscisse du lieu n'est pas, comme le dit Descartes, comptée à partir du sommet, mais bien à partir de la rencontre de l'axe des x avec une perpendiculaire, asymptote de deux branches de la courbe.

5. En ce qui concerne l'analyse du lieu « à quatre droites », que Descartes a présentée sous forme d'une discussion générale de l'équation du second degré à deux inconnues, on peut remarquer qu'il a omis de considérer le cas où le coefficient de y² est nul.

Il a lui-même reconnu cette omission et l'a signalée dans sa lettre à Debeaune du 20 fév. 1639 ;
il y fait déjà probablement allusion le 31 mars 1638, plutôt qu'au cas que nous avons supposé visé, dans la note sur ce passage.

Paul Tannery.

D'après le polycopié : Géométrie de Descartes, photocopies des éditions Adam et Tannery : IREM de Basse-Normandie (1993).

3. Solution du problème de Pappus « à quatre droites »

Dans la page des figures de Pappus, nous avons fait, avec GéoPlan, les figures des calculs de Descartes.
Ici, avec GeoGebra nous suivons les observations de la note ci-dessus, avec un repère orthonormé, d'origine A, où nous respectons les notations modernes.

Nous donnons les solutions du problème avec quatre droites : lieu des points C tel que CB × CF = CD × CH où les angles CBA, CDA, CFE et CHG sont donnés en grandeur. Pour simplifier les calculs, nous prenons tous ces angles droits.

La droite (AB) est choisie comme axe des abscisses, AB comme abscisse et CB comme ordonnée,
puis les trois droites (EF), (AD) et (GH), données de position par rapport à la première, ont pour équations ax + by + c = 0, dx + ey = 0 et fx + gy + h = 0 (avec a² + b² = 1 ; d² + e² = 1 ; f² + g² = 1).

Pour un point C(x₀, y₀), nous utilisons les mesures algébriques des projections orthogonales :

x₀ = , y₀ = , = ax₀ + by₀ + c, = dx₀ + ey₀ et = fx₀ + gy₀ + h.

Figure interactive dans GeoGebraTube : problème de Pappus

Remarque : le point C est astreint à se déplacer sur l'ellipse, grâce à la commande « Lier/libérer » du menu « point ».

Le lieu des points C tel que CB × CF = CD × CH est celui des points tel que × = λ × , avec λ = 1 et λ = – 1.

GeoGebra permet de trouver ces lieux d'équations y( ax + by + c) = λ (dx + ey)(fx + gy + h).
Ce sont deux coniques passant par quatre points situés aux intersections des droites : les points A et G sur la droite (AB), puis les points P et Q situés sur la droite (EF).

Une des deux courbes a été oubliée dans les calculs de Descartes.

Dans la résolution du problème par Descartes, la position relatives des trois dernières droites n'intervient pas et il ne s'intéresse pas au point P intersection de (EF) et (AD), ainsi qu'au point Q intersection de (EF) et (GH). Ces deux points sont pourtant des solutions évidentes du problème.

Si les segments CB, CF, CD ou CH ont des directions données par grandeur, on se ramène au cas de projections orthogonales en multipliant le coefficient λ par les rapports de similitude (sinus des angles entre les droites et les directions). Les solutions sont toujours des coniques.

4. Lieu à cinq droites dans la Géométrie de Descartes

Pages précédentes, voir : problème de Pappus

De plus, on voit ici que ce que j'ai pris pour le premier genre des lignes courbes n'en peut comprendre aucune autre que le cercle, la parabole, l'hyperbole et l'ellipse, qui est tout ce que j'avais entrepris de prouver.

Quelle est la première et la plus simple de toutes les lignes courbes qui servent à la question des anciens quand elle est proposée en cinq lignes

La Géométrie - Livre second - Page 335

Que si la question des anciens est proposée en cinq lignes qui soient toutes parallèles, il est évident que le point cherché sera toujours en une ligne droite (au moins une droite, le cas général est deux ou six lignes droites) ; mais si elle est proposée en cinq lignes, dont il y en ait quatre qui soient parallèles, et que la cinquième les coupe à angles droits, et même que toutes les lignes tirées du

On arrive à une équation de la forme x(x–a)(x–b) ± λ (x–c)(x–d) = 0 (Descartes est un peu rapide lorsqu'il affirme que c'est une droite. A-t'on deux lignes droites ou six lignes droites ?

La Géométrie - Lieu à cinq droites - Page 336

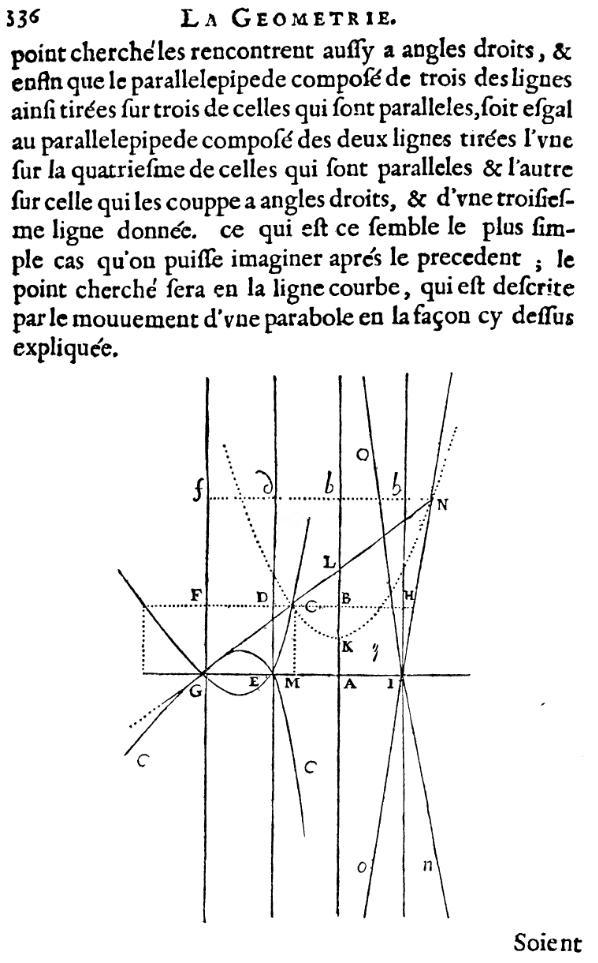
point cherché les rencontrent aussi à angles droits, et enfin que le parallélépipède (avec les notations de Tannery, le produit des longueurs A₁A₂A₃) composé de trois des lignes ainsi tirées sur trois de celles qui sont parallèles, soit égal au parallélépipède (le produit A₄A₅, simplement multiplié par GE) composé des deux lignes tirées, l'une sur la quatrième de celles qui sont parallèles, et l'autre sur celle qui les coupe à angles droits, et d'une troisième ligne donnée, ce qui est, ce semble, le plus simple cas qu'on puisse imaginer après le précédent ; le point cherché sera en la ligne courbe qui est décrite par le mouvement d'une parabole, en la façon ci-dessus expliquée.

Pour respecter la règle des homogènes, le produit A₄A₅ = CM × CB = xy est multiplié par GE = a pour obtenir, comme deuxième terme, le parallélépipède axy.

La Géométrie - Livre second - Page 337

Soient par exemple les lignes données AB, IH, ED, GF, et GA, et qu'on demande le point C, en sorte que tirant CB, CF, CD, GH et CM à angles droits sur les données, le parallélépipède des trois CF, CD et CH soit égal à celui des deux autres CB et CM, et d'une troisième qui soit AL.

Je pose GB = y, CM = x, AI ou AE ou GE = a; de façon que le point C étant entre les lignes AB et DE,
j'ai CF = 2a – y, CD = a – y, et CH = y + a ; et multipliant ces trois l'une par l'autre,
j'ai y³ – 2ay² – a²y + 2a³ égal au produit des trois autres, qui est axy.

Après cela je considère la ligne courbe CEG, que j'imagine être décrite par l'intersection de la parabole CKN, qu'on fait mouvoir en telle sorte que son diamètre KL est toujours sur la ligne droite AB, et de la règle GL qui tourne cependant autour du point G en telle sorte qu'elle passe toujours dans le plan de cette parabole par le point L.

Et je fais KL = a, et le côté droit principal, c'est-à-dire celui qui se rapporte à l'essieu (axe) de cette parabole, aussi égal à a, et GA = 2a, et CB ou MA = y, et CM ou AB = x.

Puis à cause des triangles semblables GMC et CBL, GM qui est 2a – y, est à MC qui est x, comme CB qui est y, est à BL qui est par conséquent .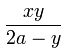

Et pourceque KL est a, BK est , ou bien .

Et enfin pourceque ce même BK, étant un segment du diamètre de la parabole, est à BC qui lui est appliquée par ordre, comme celle-ci est au côté droit qui est a, le calcul montre que
y³ – 2ay² – a²y + 2a² est égal à axy ; (la courbe est la cubique d'équation y³ – 2ay² – a²y + 2a² = axy, appelée « parabole cartésienne » par Newton et « trident de Newton » par d'autres mathématiciens.)

et par conséquent

La Géométrie - Lieu de Pappus à cinq droites - Page 338

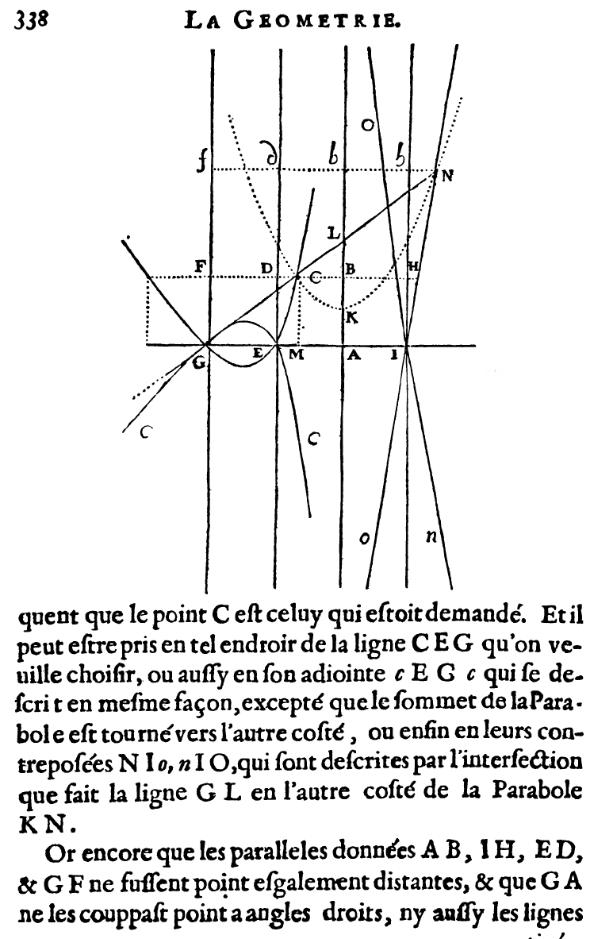
que le point C est celui qui était demandé. Et il peut être pris en tel endroit de la ligne CEG qu'on veuille choisir, ou aussi en son adjointe cEGc, qui se décrit en même façon, excepté que le sommet de la parabole est tourné vers l'autre côté, ou enfin en leurs contreposées NIo, nIO, qui sont décrites par l'intersection que fait la ligne GL en l'autre côté de la parabole KN.

Or encore que les parallèles données AB, IH, ED, et GF, ne fussent point également distantes, et que GA ne les coupât point à angles droits, ni aussi les lignes

La Géométrie - Livre second - Page 339

tirées du point C vers elles, ce point C ne laisserait pas de se trouver toujours en une ligne courbe qui serait de même nature : et il s'y peut aussi trouver quelquefois, encore qu'aucune des lignes données ne soient parallèles.

Mais si lorsqu'il y en a quatre ainsi parallèles, et une cinquième qui les traverse, et que le parallélépipède de trois des lignes tirées du point cherché, l'une sur cette cinquième, et les deux autres sur deux de celles qui sont parallèles, soit égal à celui des deux tirées sur les deux autres parallèles, et d'une autre ligne donnée : ce point cherché est en une ligne courbe d'une autre nature (Courbe d'équation axy – xy² + 2 a²x = a²y – ay², d'après Rabuel), à savoir en une qui est telle, que toutes les lignes droites appliquées par ordre (perpendiculairement à l'axe ; d'où le mot ordonnée) à son diamètre étant égales à celles d'une section conique, les segments (abscisse d'un point de la courbe) de ce diamètre qui sont entre le sommet et ces lignes ont même proportion à une certaine ligne donnée, que cette ligne donnée a aux segments du diamètre de la section conique, auxquels les pareilles lignes sont appliquées par ordre.

Et je ne saurais véritablement dire que cette ligne soit moins simple que la précédente, laquelle j'ai cru toutefois devoir prendre pour la première, à cause que la description et le calcul en sont en quelque façon plus faciles. (l'abscisse d'un point de la courbe est la quatrième proportionnelle avec l'abscisse d'un point de la conique dont l'ordonnée est la même que le point donné et une ligne donnée, voir Rabuel ?)

Pour les lignes qui servent aux autres cas, je ne m'arrêterai point à les distinguer par espèces, car je n'ai pas entrepris de dire tout ; et ayant expliqué la façon de trouver une infinité de points par où elles passent, je pense avoir assez donné le moyen de les décrire.

Pages suivantes : la méthode des tangentes