Faire de la géométrie dynamique avec GéoPlan
Faire de la géométrie dynamique avec GéoPlan
Activités avec GéoPlan/GéoSpace : des outils pour l'utilisation du logiciel de constructions géométriques.
GéoPlan au collègeTriangle, carré, cercle, rectangle Construction à la « règle et au compas » Perpendiculaires et parallèles Exercices de géométrie plane au collège |
||
|
(pages périmées) |
||
6e - 5e : |
Terminale | |
|
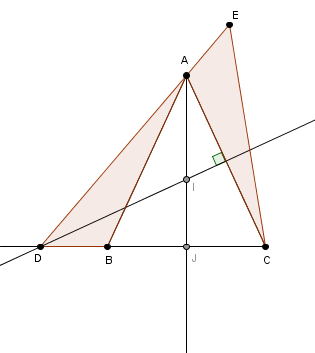
Troisième : Triangle inscrit dans un carré 4e - 2nde : Théorème de Thalès Retrouver un triangle à partir de droites remarquables Les droites remarquables du triangle Démonstrations géométriques de Pythagore Construction du pentagone régulier |
||
GéoPlan en seconde |
||
|
Ne pas confondre | |
Wikis GéoPlan GéoSpace |
Technique GéoPlan-GéoSpaceTrucs et astuces GéoPlan |
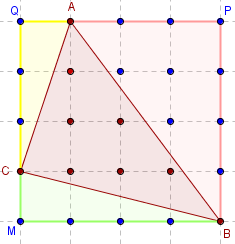
La planche à clous comme geoplan
Ne pas confondre le logiciel de géométrie dynamique, avec la construction de la planche à clous.
Logiciels gratuits de géométrie dynamique
GéoPlan/GéoSpace ou GeoGebra sont des logiciels de construction de figures mathématiques dans le plan et l'espace.
Ces logiciels de construction ont une double fonctionnalité :
- d'une part celle de création d'objets mathématiques reliés éventuellement entre eux, avec un codage très proche de leur description en langage mathématique habituel,
- d'autre part celle d'interprétation de ces objets pour en donner une représentation graphique dynamique et interactive, cette interactivité étant aussi exploitable sur Internet.
En facilitant les tracés, ces logiciels rendent la géométrie expérimentale et naturelle.
Les objets primitifs : point, droite, ligne, plan… sont implicitement définis par le tracé fait par le logiciel.
Les logiciels permettent de définir et d'utiliser des points ou objets situés hors de la figure (sans faire de zoom).
Il est possible de fabriquer des macros : prototypes avec GéoPlan qui, à partir d'objets de départ, fournissent un objet résultant.
Ce sont aussi des logiciels de géométrie analytique, avec toutes les facilités de calculs et de tracés sur les coordonnées.
Par exemple, le partage d'un segment en trois peut se faire directement en plaçant un point d'abscisse ![]() sans passer nécessairement par une construction à la règle et au compas.
sans passer nécessairement par une construction à la règle et au compas.
On peut aussi construire des fonctions et aussi investir d'autres champs mathématiques comme l'analyse.
 GéoPlan-GéoSpace
GéoPlan-GéoSpace
J'utilise l'écriture phonétique « GéoPlan-GéoSpace » que je préfère aux anglicismes « Geoplan-Geospace » ou « GeoplanW » !
Installation de GéoPlan-GéoSpace
GéoPlan-GéoSpace, logiciel libre de géométrie dynamique pour Windows 95 à XP et Vista, a été diffusé par le CRDP de Champagne-Ardenne
Télécharger GéoPlan
L'équipe du AID-CREEM, qui a développé GéoPlan-GéoSpace, vous l'offre gratuitement la dernière version pour toute utilisation pédagogique non commerciale…
Pour cela :
1 - Créer un dossier sur disque dur (nommé, par exemple, « gg » ou « geoplan-geospace »),
2 - Y télécharger les 3 fichiers compressés,
3 - Décompresser ces fichiers pour obtenir programme, librairies et aides,
4 - Créer un raccourci vers le programme « GeoplanGeospace.exe » et associer les extensions « .g2w » et « .g3w » à ce programme.
GéoPlan logiciel libre
Les sources de GéoPlan-GéoSpace étaient distribuées par Christian Mercat et l'équipe aid-creem, sous licence CeCILL.
Vous pouviez modifier ces sources, avec le logiciel Delphi, conformément à la licence et distribuer ces modifications et les exécutables créés en conservant la licence.
GéoPlan en ligne
ActiveX pour Internet Explorer sous Windows XP (version périmée)
Il n'y a pas de barre de menus, ni de boutons : double cliquer sur la figure pour avoir accès aux commandes.
Les menus fichier et option manquent.
Les contrôles ActivX ne permettent pas de charger ou d'enregistrer une figure.
Travailler en « copier-coller » en swapant entre l'éditeur du texte de la figure et un traitement de texte ou un éditeur de pages html. De même, les images se copient et s'impriment dans un logiciel spécifique comme Paint.
Faire de la géométrie dynamique
Mon projet de fin de carrière fût, avec GéoPlan, de mettre en forme une centaine de figures clefs.
Au fil des années, s'est constituée une base d'exercices présentant la moitié des figures de géométrie synthétique réalisées avec GéoPlan dans l'enseignement secondaire.
Dans 200 pages couvrant l'ensemble des chapitres de la géométrie classique l'application « Faire de la géométrie dynamique » présente 1 500 exercices de géométrie.
C'est une synthèse des activités des classes de 6e à la terminale.
Ces documents sont destinés à l'usage des élèves et à la documentation des professeurs de mathématiques.
Chaque page contient une dizaine d'exercices réalisés avec GéoPlan avec les fichiers en téléchargement. Des figures GeoGebra peuvent aussi être téléchargées.
Interactivité de GéoPlan-GéoSpace
pages périmées
Les anciennes pages sont aussi diffusées avec les contrôles ActiveX qui permettaient de rendre les figures interactives, mais en raison des difficultés avec Vista, le développement est stoppé et la version interactive n'est plus mise à jour depuis 2007.
Mes exemples sont souvent pilotables au clavier : appuyez sur les flèches de déplacement pour mouvoir un point caractéristique.
Le clic droit glissé translate la figure GéoPlan, le clic droit permet de la faire tourner une figure GéoSpace.
En général, dans mes figures GéoSpace la touche W permet de revenir à la vue initiale et la touche F permet d'obtenir une vue de Face.

La géométrie dynamique
Les logiciels de géométrie permettent une approche dynamique de la construction de figures et par la mise en valeur d'invariants facilitent la résolution de problèmes. De plus, dans le cas de la géométrie dans l'espace en particulier, GéoSpace est une source de visualisation et, à ce titre, contribue à la formation donnée aux élèves.
Initiation à GéoPlan
Le plus simple est de commencer par les exercices de sixième.
• Réaliser les figures de base et faire les exercices,
• en cas problème, télécharger la figure et en éditer le texte de figure pour comprendre.
Continuer ensuite en choisissant divers exercices dans les pages pour le collège.
Humeur et tableau noir – Plot n°25
Faire des mathématiques avec GéoPlan
Effets observés de l'introduction de l'outil informatique sur l'enseignement et sur l'activité des élèves en groupes (modules, TD etc.)
Lorsque la configuration le permet, les professeurs organisent quelques séances en salle d'informatique. Schématiquement, on peut voir que des activités de deux types sont alors proposées :
- Résolution de problèmes : modélisation – expérimentation sur ordinateur ou calculatrice – conjecture – démonstration tout ou partie effectuée par les élèves.
Ce type d'activité est au centre du travail mathématique et donc de la formation de l'élève. Il faut, pour cela, veiller à laisser à l'élève une autonomie suffisante pour qu'il puisse se livrer à des essais, chercher, découvrir, se tromper, apprendre à contrôler son travail (et l'outil informatique apporte alors bien souvent une aide décisive). Il est donc essentiel que la façon dont l'activité est présentée permette une véritable découverte et suscite de véritables questions. C'est à cette condition que le travail mathématique peut véritablement s'installer.
Il faut donc proscrire les présentations d'activités qui ne laissent plus à l'élève que la responsabilité d'effectuer chacune des microtâches indiquées sur la fiche. - Des exercices d'entraînement et/ou de remédiation.
Les mathématiques et la géométrie
Depuis 30 siècles les mathématiques oscillent entre calcul et raisonnement.
Quand un Mésopotamien attaque une division, il sait qu'il aboutira, ce n'est guère ludique et il peut même évaluer le temps approximatif qu'il mettra !
Quand un pythagoricien aborde un problème de géométrie, il ne sait pas combien de temps il « séchera », et même s'il trouvera un jour ! Mais quelle joie lorsqu'il trouve.
Le mythe de la méthode de Descartes était de « diviser chacune des difficultés que j'examinerai en autant de parcelles qu'il se pourrait et qu'il serait requis pour les résoudre » et tous les problèmes de géométrie peuvent se réduire à des calculs sur des nombres. Génial en 1637, mais cela ne marche pas.
L'enseignement des mathématiques doit être repensé en raison des mauvais résultats de nos élèves et du rejet de la matière par nombre d'entre eux, avec une majorité de filles.
Il faut recentrer le cursus mathématique sur les problèmes réels et cet enseignement doit contribuer à l'« alphabétisation numérique ».
On ne fait plus de mathématiques sans outils informatiques. Ce n'est pas le plus simple, surtout pour les enseignants, et on cumule les difficultés :
• les maths,
• l'informatique qui n'est pas moins abstraite que la mathématique,
• sans oublier le problème des effectifs : un enseignant ne peut travailler sur plus de 8 postes, avec au maximum deux élèves par ordinateur ;
ceci est peu compatible avec le bourrage actuel des classes et la suppression des groupes à effectif réduit.
La géométrie
Bien que devenue pratiquement absente de l'enseignement secondaire, la géométrie est de plus en plus présente dans notre civilisation de l'image (virtuelle), mais sans bonnes images mentales, on ne peut bien travailler dans « l'espace fonctionnel » : même devant l'ordinateur, on ne peut faire des maths (et de la géométrie non euclidienne) qu'en dessinant des schémas avec un crayon, dans le plan euclidien d'une feuille.
Les axiomes comme l'« unicité d'une parallèle » ou les « cas d'égalité des triangles » ont été explicités par Euclide et fournissent un fondement de la géométrie, imparfait certes, mais sur lesquels les autres résultats reposent solidement.
Avec la méthode synthétique, Euclide a organisé la géométrie de manière déductive en donnant, à partir des propriétés géométriques établies précédemment, un raisonnement pour déduire chaque propriété cherchée.
Contrairement aux spéculations de Bourbaki sur la mort d'Euclide, de nombreux problèmes de géométrie, d'apparence simple :
• sont toujours non résolus, ou résolus récemment au prix de difficultés considérables,
• pour être compris, demandent un degré d'abstraction bien supérieur à celui de leur énoncé,
• les outils mathématiques utilisés pour les résoudre ont été conçus ou serviront dans de tout autres buts.
La géométrie doit être enseignée :
• elle est belle, utile et infinie,
• il est indispensable d'avoir une vision géométrique,
• elle est le lieu privilégié de l'apprentissage de la recherche, de l'imagination et de la rigueur,
• les logiciels de géométrie dynamique libèrent de l'imperfection des figures. Ces figures sont facilement modifiables et affranchies de la difficulté des calculs ; la maîtrise du logiciel est une bonne formation à l'informatique.
Le site « Descartes et les Mathématiques »
Le site présente des activités géométriques de la 6e à la terminale.
Dans la mesure du possible, mes figures sont constructions ou des recherches de niveau élémentaire, mais non évidentes, où la géométrie dynamique est pertinente.
Ma pratique est de :
• Réaliser une figure :
devant un problème de géométrie, je fais une figure sur mon ordinateur, c'est déjà une activité formatrice.
• Rechercher une solution :
la figure faite, j'étudie les invariants ; je vérifie quelques conjectures et souvent je me contente de la preuve par GéoPlan !
Autrefois, je ne publiais que des imagiciels nus, la figure dynamique se suffisant à elle-même.
Petit à petit, en raison de la nature même d'Internet, où l'interactivité, y compris dans les wikis, est bien moindre que ce que l'on pourrait penser, j'ai été amené à proposer une recherche davantage guidée, abrégeant la démarche expérimentale.
Les indications de recherche et les solutions sont, dans la mesure du possible, données dans divers cadres : géométrie synthétique, isométries ou similitudes…,
en évitant la géométrie analytique (calculs sous-entendus par le logiciel) et en essayant d'identifier les transferts entre domaines.
• Faire des démonstrations :
La place de la démonstration en géométrie est souvent exagérée. On a dû se résigner à pratiquement ne plus en faire du Collège et à la première. Quelle est sa place véritable en Terminale S ?
Elle n'apporte pas forcément grand-chose de plus, surtout si elle se réduit, comme dans trop de problèmes de bac, à un calcul analytique ou avec les nombres complexes, alors que le contexte géométrique est complètement occulté
La démonstration rassure le professeur…, mais il faut sérieusement repenser sa place dans le contexte de la géométrie dynamique, pour qu'elle retrouve attractivité et légitimité.
La position de l'inspection est assez schizophrène : entre incitation à en faire et suppression dans les programmes.
• Origine et téléchargement
Les exercices sont tirés de mes cours, de mes lectures ou de manuels.
Ils ont été le plus souvent adaptés ou réécrits et, en général, la figure est mon œuvre personnelle ;
Lorsque ce n'est pas original, les sources sont citées.
Tous les exercices sont libres, librement modifiables, et proposés au téléchargement avec GéoPlan/GéoSpace ou GeoGebra.
Ils sont proposés à l'état brut, sans scénario pédagogique, ni animation.
Étant à la retraite, je n'ai pas réalisé que très peu de ces figures avec des élèves.
• Organisation multicritère
Mes pages « .html » sont formées de quatre à une dizaine d'exercices proposés avec énoncés, figures et solutions.
Les exercices y sont regroupés :
– par thème : constructions, inscription, contact, optimisation, transformations, lieu, triangle, polygones, espace ;
– par niveau : de la sixième à la terminale, après-bac, Capes et ce qui a été retiré des programmes ;
– selon des critères historiques : Antiquité, Euclide, Descartes,
grands théorèmes et culture mathématique.
Divers menus permettent de naviguer dans le site et Google y est très à l'aise.
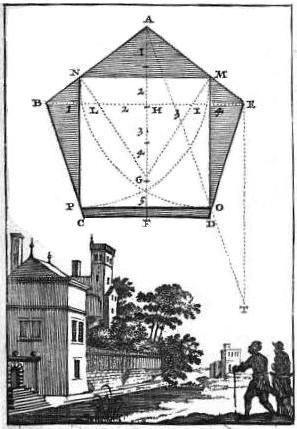
Image ci-contre de Sébastien Leclerc : Traité de géométrie théorique et pratique
• Histoire des mathématiques
Retrouver des figures anciennes est un plus et permet d'introduire une perspective historique dans l'enseignement
(voir les mathématiciens cités dans le site).
• WikiPédia
J'ai inséré de nombreuses figures dans WikiPédia (géométrie du triangle) et dans les forums où trop d'énoncés sont donnés sans images.
• Liens et rétroliens
De nombreux liens sont proposés vers d'autres sites et vers Google qui assure 80 % de la diffusion.
Il y a peu de collaboration et peu de feedback, même sur les Wikis.
• GeoGebra comme Outil de Présentation
J'utilise GeoGebra et ses feuilles de travail dynamique comme logiciel de présentation pour la géométrie.
J'espère que les solutions proposées sur mon site stimuleront l'intérêt des collègues et pourront les convaincre d'intégrer la géométrie dynamique au cours de mathématique.
Mais avec la suppression de l'épreuve pratique et la dégradation des programmes de géométrie du lycée, la majorité de mes pages pour la première et la terminale sont maintenant hors programme.
La géométrie au lycée se réduit maintenant au calcul ou à la répétition des exercices de collège !
Je suis très triste des évolutions de l'enseignement, en général, et de la géométrie en particulier.
|
Rétroliens (backlinks) Régis DELEUZE : Apprendre à utiliser Géoplan & Géospace Google attribue faussement cette page à : www.eu/search?q=nombres fl%26#232;ches gratuits | |
|
Page créée le 23/3/2011 | |
 WikiPédia
WikiPédia