Descartes et les Mathématiques

Courbes de poursuite - Les quatre chiens

Simulation de processus dynamiques : création itérative en 1^ère S avec GéoPlan.

Sommaire

1. Problème des quatre chiens

2. Figures itératives : carrés gigognes

3. Étude d'une suite tendant vers 0

4. Figures itératives : polygones réguliers

a. triangles gigognes

b. pentagones gigognes

5. Retour sur les carrés emboîtés

Étude d'une suite tendant vers 1

6. Courbes du chien

Mobile friendly: sur tablette numérique ou smartphone, bascule automatique vers la version mobile

Les problèmes des chiens sont des problèmes de poursuite et d'interception, dans lesquels on cherche les trajectoires et les points de rencontre de chiens, placés initialement aux coins d'un polygone régulier.

1. Figures géométriques et concept de limite

Courbe de poursuite

C'est Léonard de Vinci qui étudia le premier les problèmes de poursuite. Ce sont des problèmes idéaux pour les ordinateurs, qui se décrivent facilement à l'aide d'algorithmes simples.

Peut être l'objet d'un chapitre d'une leçon, hors sujet, de l'agrégation (que j'ai raté trois fois !).

Énoncé
Quatre chiens, quatre mouches, quatre scarabées, quatre lièvres, quatre tortues ou quatre souris (pour les anglophones : four mice problem ; four bugs, four spiders…) : moult versions pour un même problème…

On suppose que quatre chiens identiques « au sens mathématique du terme » sont situés aux quatre sommets d'un carré ABCD. Le chien A se met à courir en direction du chien B, qui lui-même court en direction du chien C, le chien C vers le chien D et le chien D vers le chien A.

La vitesse des chiens est constante en norme. Au fur à mesure des déplacements les chiens parcourent des segments de droite et modifient leurs trajectoires pour rester en direction de leur cible.

Ce problème, important en balistique pour l'étude de la poursuite de missiles, a été étudié au XIX^e siècle et nous allons le simuler avec GéoPlan.
Ne pas confondre cette application des suites à la géométrie avec les suites géométriques, étudiées en analyse.

Situation
A chaque déplacement une fraction k de la longueur du côté du carré est parcourue.
Étant donné un nombre k compris entre 0 et 1, on considère la suite des carrés obtenus à partir d'un premier carré A₀B₀C₀D₀ par l'algorithme suivant : le carré numéro n + 1 est obtenu à partie du carré numéro n en plaçant dans le repère (A_n, A_nB_n) le point A_n+1 d'abscisse k et en faisant de même pour les trois autres côtés.

Figures itératives avec GéoPlan

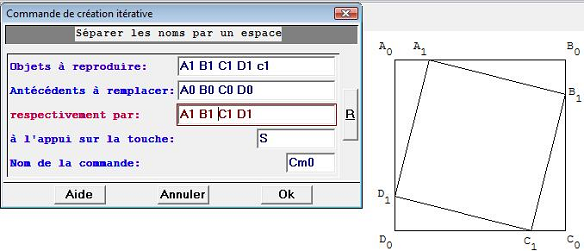
Commentaires sur la réalisation
Cet exercice est réalisé avec une commande de création itérative.
Supposons créés les deux premiers carrés : A₀B₀C₀D₀ appelé c₀ et A₁B₁C₁D₁ appelé c₁.
Une commande de création itérative demandant de reconstruire A₁ B₁ C₁ D₁ et c₁ en changeant A₀ B₀ C₀ D₀ respectivement en A₁ B₁ C₁ D₁ donnera, par l'appui sur la touche S choisie, un nouveau carré A₂B₂C₂D₂ appelé c₂ (les noms avec 2 en indice sont donnés automatiquement par GéoPlan). Encore un appui, sur cette même touche S, donnera un nouveau carré, construit de la même façon et nommé c₃ également automatiquement, etc.

2. Figures itératives : carrés gigognes

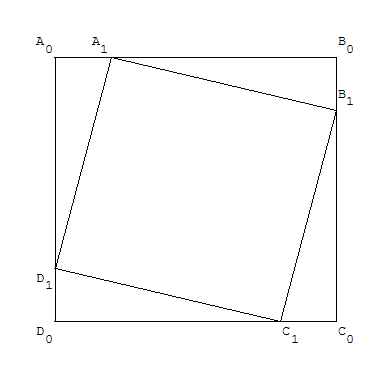
Première figure itérative

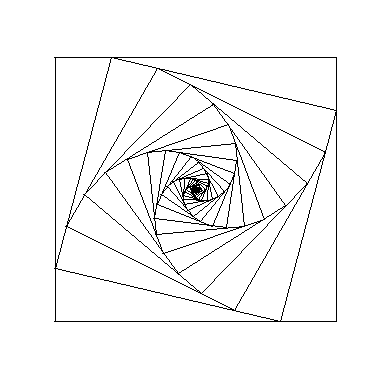
Résultat de l'itération

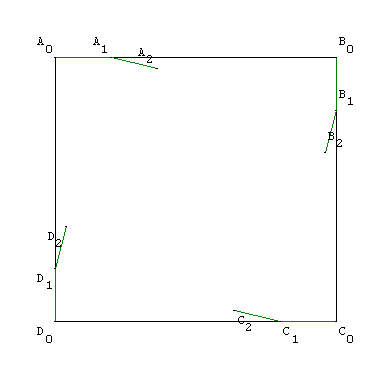
télécharger la figure GéoPlan chien4_1.g2w

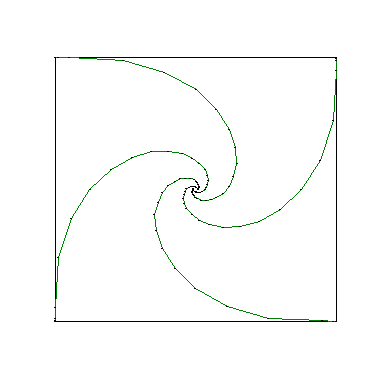
Les chiens tracent quatre spirales logarithmiques dont le centre est celui du carré et de longueur égale au côté du carré.

 télécharger la figure GéoPlan chien4_8.g2w

3. Calculs

Associons à ce problème la suite a des mesures des côtés des carrés a_n = A_nB_n

Choisissons comme unité de longueur A₀B₀, le côté du premier carré, soit a₀ = 1.

Cas particulier k =

Dans le triangle rectangle A₁B₀B₁ d'après la propriété de Pythagore, on a  :
A₁B₁² = A₁B₀² + B₀B₁² = = .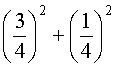

a₁ = A₁B₁ = , a₂ = A₂B₂ = .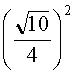
La suite (a_n) des longueurs des côtés des carrés est une suite géométrique de premier terme a₀ = 1 et de raison λ = .

Les aires des carrés sont s₀ = 1, s₁ = , s₂ = … ; (s_n) est une suite géométrique de premier terme s₀ = 1 et de raison .

Le chien situé en A parcourt les longueurs b₀ = A₀A₁ = , b₁ = A₁A₂ = , b₂ = A₂A₃ = …

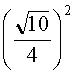La trajectoire parcourue par le chien A est la ligne polygonale A₀A₁A₂A₃ … A_n-1A_n. Elle a pour longueur :
t_n = b₀ + b₁ + b₂ + … + b_n-1 = 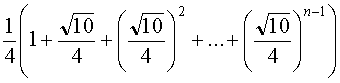somme des n premiers termes d'une suite géométrique b_n de premier terme b₀ = et de raison λ = .
Cette somme est égale à = .

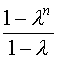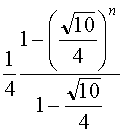Comme λ est compris entre 0 et 1, lorsque n tend vers +∞, λⁿ tend vers 0,
la limite est égale à = 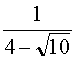≈ 1,19 ; c'est la longueur d'une trajectoire.

Cas général

Dans le triangle rectangle A₁B₀B₁, d'après la propriété de Pythagore, on a :
A₁B₁² = A₁B₀² + B₀B₁² = (1 –k)² + k² = 1 - 2k + 2k².

La suite (a_n) des côtés des carrés est une suite géométrique de premier terme a₀ = 1
et de raison λ = .

La suite (s_n) des aires des carrés est une suite géométrique de premier terme s₀ = 1 et de raison 1 - 2k + 2k².

La ligne polygonale A₀A₁A₂A₃ … A_n-1A_n parcourue par le chien A a pour longueur t_n = b₀ + b₁ + b₂ + … + b_n-1 somme des n premiers termes d'une suite géométrique de premier terme k et de raison λ = . Cette somme est t_n = k.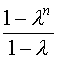

Comme λ est compris entre 0 et 1, lorsque n tend vers +∞, λⁿ tend vers 0, la limite est égale à :
l_k = k = 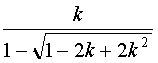. Cette limite représente la longueur d'une trajectoire.

Approximation de l_k

Le chemin idéal où le chien modifie sa trajectoire à tout instant correspond au cas où k tend vers 0.

Pour calculer la limite de l_k lorsque k tend vers 0, nous connaissons en 1^ère S, lorsque x est « petit », les approximations affines :
≈ 1 + et ≈ 1 + x.

Ici nous devons développer la racine à l'ordre 2, avec par exemple sur la TI-92 la fonction taylor(Ö(1+x),x,2),
et utiliser ≈ 1 + - . En remplaçant x par - 2k + 2k² et en négligeant les termes supérieurs au degré 2 {ou directement sur la TI-92 avec la fonction taylor(Ö(1-2*k+2*k^2),k,2) } on obtient ≈ 1 - k + .

Donc, l_k = 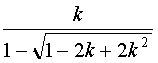≈ ≈ ≈ ≈ 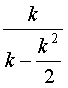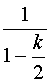1 +

Lorsque k tend vers 0, a pour limite 0, l_k tend vers 1. La longueur d'une trajectoire est égale au côté du carré.
On a donc une courbe « illimitée » qui a pourtant une longueur finie. Cette courbe admet un « point limite » qui par raison de symétrie est le centre O des carrés.

Encadrement de l_k

Pour démontrer, utilisons l'encadrement 1 - k < < 1 - k + k².

On a (1 - k + k²)² = 1 - 2k + 3k² - 2k³ + k⁴ et en élevant au carré la double inégalité :

1 - 2k + k² < 1 - 2k + 2k² < 1 – 2k + 2k² + k²(1 – k)². Les différences entre les termes sont les nombres positifs k² et k²(1 – k)². Ces inégalités sont bien vérifiées.

d'où k <1 - < k - k² et 1 < < .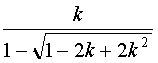

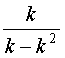Donc, 1 < l_k < . Si 0 < k < , alors < 1 + 2k.

1 < l_k < 1 + 2k, lorsque k tend vers 0, 1 + 2k a pour limite 1 et, d'après le théorème des gendarmes, l_k tend vers 1. La longueur d'une trajectoire est bien égale au côté du carré.

4. Figures itératives : polygones réguliers

Plus généralement, le problème des chiens est un problème de poursuite et d'interception dans lequel on cherche le point de rencontre de chiens, placés initialement aux coins d'un polygone régulier.

Les chiens se déplacent à la même vitesse constante en norme. Au fur et à mesure des déplacements les chiens parcourent des segments et modifient leur trajectoire pour rester en direction de leurs cibles.

Les chiens tracent des spirales logarithmiques dont le centre est celui du polygone et de longueur égale au côté du polygone.

4.a. Triangles gigognes

Première figure itérative

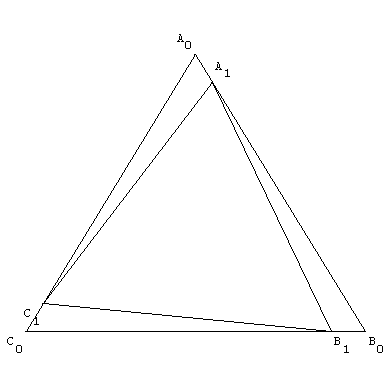
Résultat de l'itération

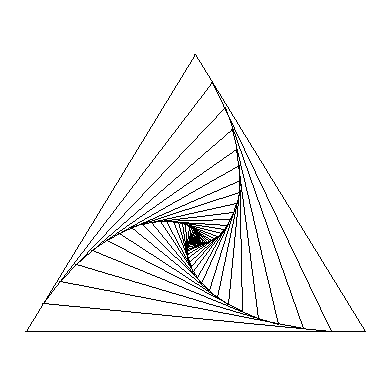
: télécharger la figure GéoPlan chien3_1.g2w

4.b. Pentagones gigognes

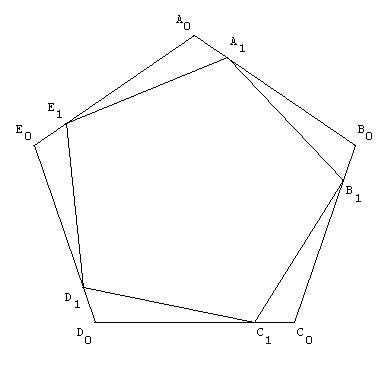
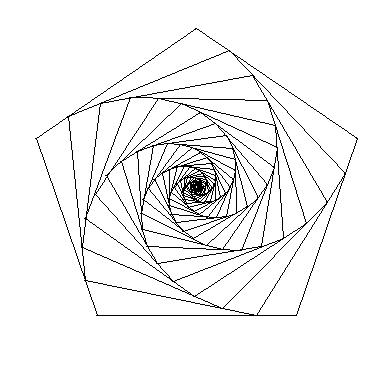
télécharger la figure GéoPlan chien5_1.g2w

5. Retour sur les carrés emboîtés

Autre forme d'après la brochure d'accompagnement des programmes de 1^ère S : la suite obtenue n'est ni arithmétique, ni géométrique, une formule explicite ne peut se conjecturer facilement et la limite n'est pas nulle.

À chaque étape du déplacement, la longueur parcourue sur le côté du carré est d'une unité.

On part d'un carré A₀B₀C₀D₀ de côté 10 unités. Sur chaque côté, en tournant dans le même sens, on place un point situé à la distance 1 de chaque sommet du carré. On obtient le carré A₁B₁C₁D₁, et on itère…

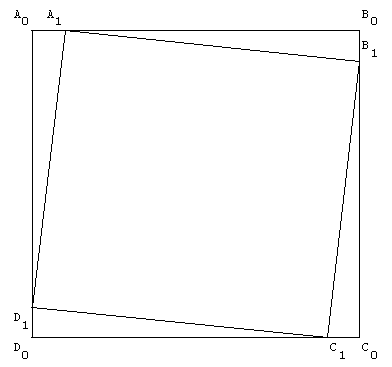
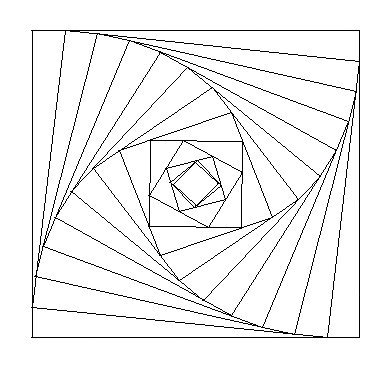
Télécharger la figure GéoPlan car_em_1.g2w

On obtient des carrés de plus en plus petits, mais on a l'impression que cela s'arrête.

Nous admettrons que tous les quadrilatères sont des carrés.

Soit u_n la longueur du côté du carré A_nB_nC_nD_n avec u₀ = 10.
Le théorème de Pythagore, dans le triangle A_n+1B_nB_n+1, rectangle en B_n, permet d'écrire :
u_n+1² = (u_n - 1)² + 1 ;
u est donc la suite définie par récurrence par u₀ = 10 et u_n+1 = .

Voici les calculs effectués avec un tableur :

On remarque que pour GéoPlan les résultats se stabilisent à partir de n = 12 : l'affichage de A_n+1 est confondu avec B_n. Le tableur affiche la valeur approchée 1 à partir de n = 15. Les chiens ne se rattrapent pas, mais tournent sur les bords de carrés de côtés de longueurs voisinent de 1.

Mais on peut démontrer que pour tout n, u_n ≥ 1, et montrer par l'absurde que u_n ≠ 1, donc u_n > 1.
En déduire que u est une suite décroissante.

Pour montrer que la suite u est convergente vers l = 1 solution de l'équation :
l = , nous utiliserons la suite auxiliaire v telle que v_n = u_n - 1, où v_n représente la longueur de A_n+1B_n :

v est une suite décroissante dont tous les termes sont strictement positifs.
Pour tout n ≥ 0, on a v_n+1 <

Démonstration de ces inégalités par comparaison de carrés :

(v_n+1 + 1)² = u_n+1² = (u_n - 1)² + 1 = v_n² + 1 est à comparer avec ( + 1)² = v_n⁴/4 + v_n² + 1

Comme 0 < v_n²/4, on a v_n² + 1 < v_n⁴/4 + v_n² + 1
et puisque le membre de gauche vaut (v_n+1 + 1)² et le membre de droite vaut ( + 1)²,
on obtient l'inégalité : (v_n+1 + 1)² < ( + 1)².
En raison de la croissance de la fonction racine, par extraction de la racine de ces termes positifs : v_n+1 + 1 < + 1
et enfin, par soustraction de 1, v_n+1<  ; d'où l'assertion.

Application des inégalités

Comme v₁₀ < 1, on a v₁₁ << et pour n ≥ 10, v_n+1 << ,
donc pour n ≥ 10 on a 0 < v_n < .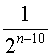
La suite v de termes positifs, majorés par une suite géométrique de limite nulle, a une limite égale à 0.
La suite u, telle que u_n = v_n + 1, a une limite égale à 1.

6. Laisser donc courir le chien - Courbes du chien

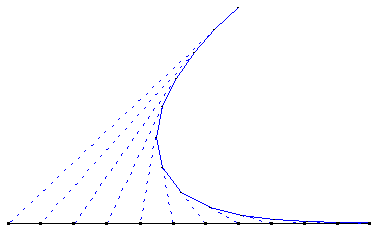
Le chien de Léonard Euler

Un chien a l'habitude de courir avec son maître.
Il s'efforce d'aller vers lui, mais comme ce dernier se déplace, il modifie régulièrement sa trajectoire, en progressant par bonds successifs.
Le chien et le maître courent à la même vitesse.

Ci-contre : tractrice, courbe du chien lorsque le maître se déplace sur une droite.

Télécharger la figure GéoPlan maitre_droite.g2w

Courbe du chien lorsque le maître se déplace sur un cercle.

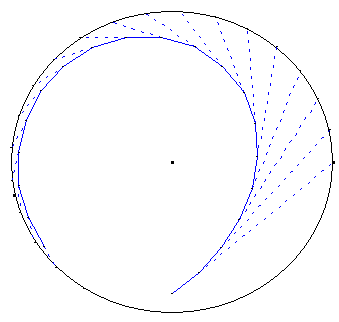
Télécharger la figure GéoPlan maitre_cercle.g2w

Bibliographie

De la courbe que décrit un chien en courant après son maître - Jean Baptiste Touchard – Patrick Huet - IREM de Paris Sud
 Tortues : Haha ou l'éclair de la compréhension mathématique - Martin Gardner - Pour la science - Belin - 1979
Exercices dans de nombreux manuels scolaires.

Table des matières

Liens - Rétroliens

Quatre mouches sur un carré : des propositions d'équations différentielles pour trouver une trajectoire (de longueur égale au côté du carré).

bibmath.net/forums/

Téléchargement

Télécharger courbe_du_chien.pdf : ce document au format « .pdf »

Google considère l'UR comme une erreur de type "soft 404" .

Page n^o 38, réalisée le 1/4/2003
mise à jour le 25/3/2014