Descartes et les Mathématiques

Pyramide régulière de base octogonale

La géométrie dans l'espace en seconde avec GéoSpace.

Sommaire

1. Construction d'un octogone régulier à partir d'un côté
2. Pyramide régulière de base octogonale
3. Maison
    solide formé par l'assemblage d'un prisme et d'une pyramide
4. Problème concret : abris de jardin

GéoPlan : Constructions de l'octogone

1. Construction d'un octogone à partir d'un côté

Classe de première L

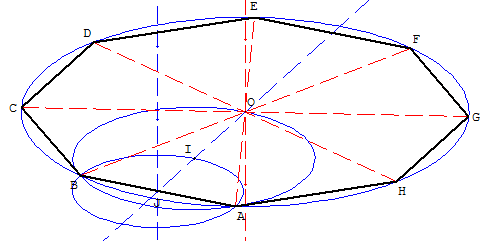
Du centre O du cercle circonscrit, on « voit » un côté [AB] suivant un angle de 45°.
Le point O est situé sur arc capable correspondant à un angle au centre de 90°.
Le centre I de l'arc capable est donc situé sur le cercle de diamètre le côté [AB].

Construction dans un plan (p)

Étant donné deux points A et B d'un plan (p), dans ce plan, tracer le cercle de diamètre [AB], la médiatrice de [AB] coupe ce cercle en un point I.

Technique GéoSpace : pour tracer la médiatrice de [AB], tracer un axe perpendiculaire au plan (p) en J milieu de [AB]. Le point A a pour image I par la rotation d'angle 90° par rapport à cet axe. La droite (JI) est la médiatrice de [AB].

Le cercle de centre I, passant par A, coupe la médiatrice en un point O, situé du même côté que I par rapport à (AB).

AÔB = AÎB = 45°, le point O est le centre du cercle circonscrit à l'octogone.

On termine la construction de l'octogone ABCDEFGH en traçant un axe (d) perpendiculaire au plan (p) en O et en traçant les divers sommets par des rotations d'angle 45° autour de cet axe.

Télécharger la figure GéoSpace octogone.g3w

2. Pyramide régulière de base octogonale

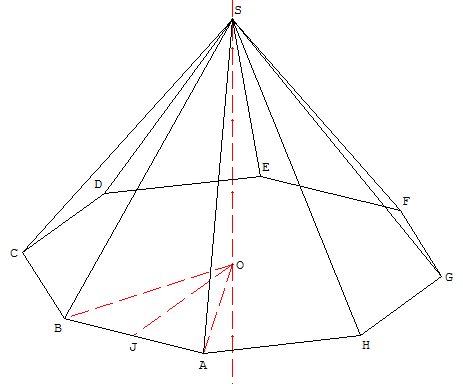
Reprendre la construction de l'octogone régulier ABCDEFGH ci-dessus.
Sur la droite (d) perpendiculaire en O, milieu de l'octogone, au plan (OAB), placer un point S et tracer le solide ABCDEFGHS.

Télécharger la figure GéoSpace pyramide_octogone.g3w

3. Maison octogonale

Solide composite formé par l'assemblage d'un prisme et d'une pyramide

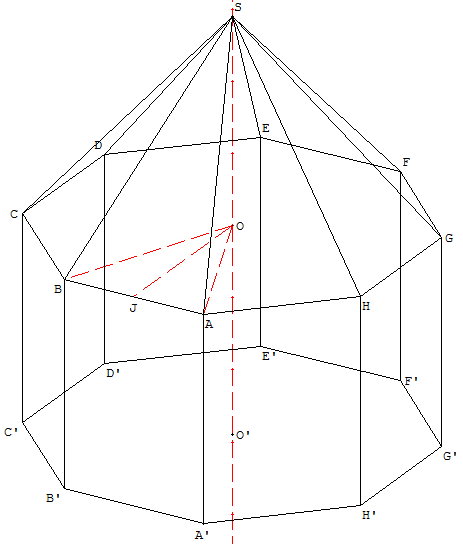
Reprendre la construction de la pyramide octogonale ABCDEFGHS ci-dessus.
Sur l'axe (OS) de la pyramide, placer un point O’.

Avec la translation transformant O en O’, tracer l'octogone A’B’C’D’E’F’G’H’,
terminer en traçant le solide A’B’C’D’E’F’G’H’ABCDEFGHS réunoin d'une pyramide octogonale et d'un prisme octogogonal A’B’C’D’E’F’G’H’ABCDEFGH.

Télécharger la figure GéoSpace maison_octogone.g3w

4. Problème concret : abri de jardin

Bonjour, je me permets de vous contacter, car je ne sais pas comment résoudre ce problème :

Comment calculer l'aire pour une toiture de forme octogonale sachant que celle-ci a un degré d'inclinaison de 45° ?
L'octogone est régulier, et fait 2,30 m pour chaque côté.
Je vous joins un dessin de la structure.

J'espère que vous prendrez le temps de vous poser sur mon problème.
Si c'est le cas, j'aimerais que vous me donniez tous les détails de calculs pour pouvoir l'effectuer à l'avenir puisque ceci me sert professionnellement : mon métier est la construction d'abris de maison.

ABCDEFGH est un octogone régulier de côté AB = 2,3 m.

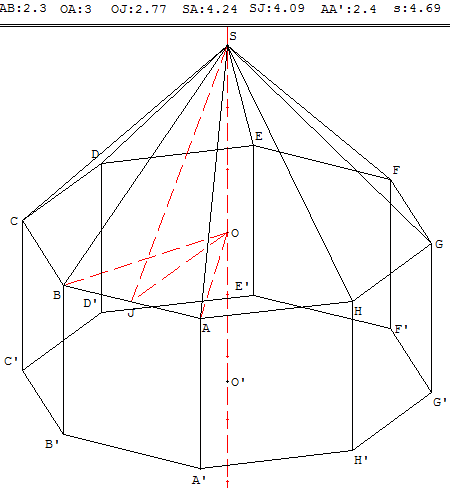
En fonction du rayon r = OA du cercle circonscrit, la longueur du côté est : 2 r sin 22,5° = r ≈ 0,765 r (calcul du sinus : angle trigonométrie).
En inversant on trouve le rayon en fonction du côté : r ≈ 1,306 AB, d'où r = OA = 3 m.

Si J est le milieu de [AB], l'apothème de l'octogone est OJ = r cos 22,5° = r ≈ 0,924 r, soit OJ = 2,77 m.

Lorsque OÂS = 45°, l'angle dièdre du toit et du plan horizontal est l'angle OJS alors égal à 47,3° ; on calcule la longueur JS par la relation de Pythagore dans le triangle rectangle OJS.

L'aire du triangle SAB est la moitié du côté AB multiplié par la hauteur JS = 2,77 m d'où 4,69 m².
Soit une toiture de 37,5 m².

Remarque :
ces calculs ne tiennent pas compte du débord de la toiture par rapport à la base. Pour un débord de k %, augmenter les aires de k² %.

Télécharger la figure GéoSpace abris_octogone.g3w

Table des matières

Dans d'autres pages du site

…Avec GéoSpace

3^e: Sections de cube, pyramide

2^nde : tétraèdre

Coin de cube

1^ère S GéoSpace Activité

Polyèdre

Mobile friendly