Descartes et les Mathématiques

Puissance d'un point
par rapport à un cercle

Géométrie du cercle pour l'après-bac

Sommaire

1. Puissance d'un point par rapport à un cercle

2. Application : orthocentre

3. Application de la théorie de l'axe radical

4. Différence des puissances d'un point pour deux cercles

5. Relation d'Euler

6. Premier théorème de la médiane

1. Définition et propriétés de la puissance d'un point

en : power of a point
de : Die Potenz eines Punktes bezüglich eines Kreises

La puissance d'un point par rapport à un cercle
a été introduite par Jakob Steiner en 1830

Notion que j'enseignais en troisième en 1970,
maintenant disparue de l'enseignement français au lycée.

1.a. Théorème d'Euclide

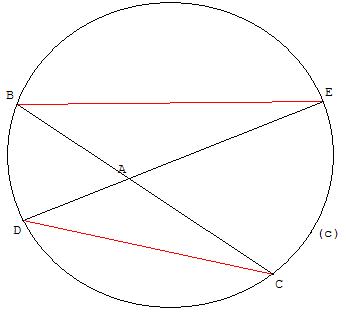
Si deux droites, passant par un point A, coupent un cercle (c),
l'une en B et C, l'autre en D et E, on a :

AB × AC = AD × AE.

Dans le cas où A est à l'intérieur du cercle, pour le démontrer,
il suffit de remarquer que les triangles ABE et ADC sont semblables,
ayant leurs angles en A opposés par le sommet
et leurs angles inscrits BCD et BÊD égaux.
En écrivant l'égalité des rapports = ,
on conclut avec le produit des « extrêmes » égal à celui des « moyens ».

Puissance d'un point extérieur à un cercle et tangente

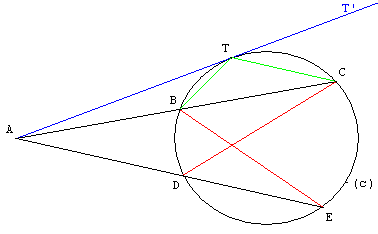
Lorsque A est à l'extérieur du cercle, avec une tangente (AT), on a :

AB × AC = AD × AE = AT².

Remarque : les cordes (CD) et (BE) sont antiparallèles
aux côtés de l'angle CAE.

1.c. Définition

Pour un point A extérieur à un cercle (c),
la puissance du point A par rapport au cercle est le produit AB × AC,
où une sécante issue de A coupe le cercle en B et C.
Cette puissance est constante lorsque la droite varie.
Elle est égale au carré de la longueur AT d'une tangente au cercle issue de A :

AB × AC = AT².

Elle est aussi égale à la différence du carré de la distance
du point au centre du cercle moins le carré du rayon :

AB × AC = AO² – OT² = d² – r².

On note c(A) = AO² – r² la puissance de A par rapport à (c).

Si le point A est sur le cercle, la puissance est nulle : c(A) = 0.

Si le point A est à l'intérieur du cercle, la puissance est négative :

c(A) = – AB × AC = d² – r².

Mesures algébriques

Quel que soit le point A, la puissance du point A par rapport au cercle
est le produit  × .

Réciproques

• Si les droites (BC) et (DE) se coupent en un point A
  et qu'on a AB × AC = AD × AE
  (avec l'ordre des points A, B, C le même que l'ordre des points A, D, E),
  alors les points B, C, D et E sont cocycliques.
• L'égalité AB × AC = AT² est suffisante pour affirmer
  que la droite (AT) est tangente au cercle.

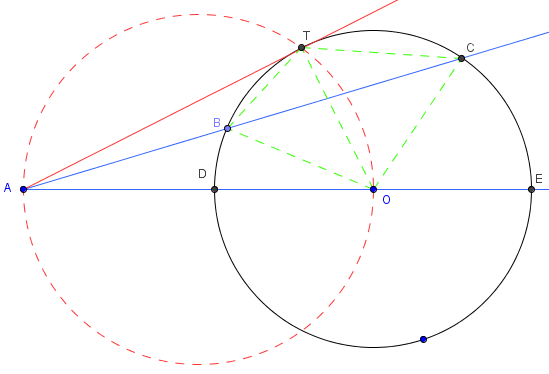
Démonstration : angles inscrits et triangles semblables
– A extérieur au cercle

L'angle inscrit CBT interceptant l'arc CT est égal
à l'angle de la corde [TC] et de la tangente (TT’).
Les angles supplémentaires ABT et ATC sont aussi égaux
et les triangles ABT et ATC ont cet angle égal et l'angle A en commun :
ils sont donc semblables.

Des rapports de similitude égaux = on déduit,
avec l'égalité des produits des « extrêmes »
et des « moyens », que AB × AC = AT².
Il résulte que le produit AB × AC ne dépend pas
de la sécante, mais seulement du point A.

En particulier pour la sécante (AO) la puissance du point A est aussi
AD × AE = (AO – OD) × (AO + OE) = AO² – OE² = d² – r².
Résultat conforme à la relation de Pythagore dans le triangle rectangle AOT.

Figure interactive dans GeoGebraTube :
     puissance d'un point par rapport à un cercle

Cercles tangents à des droites ou à des cercles : voir construction de cercles

Moyenne géométrique : construction de Wallis

2. Application : orthocentre

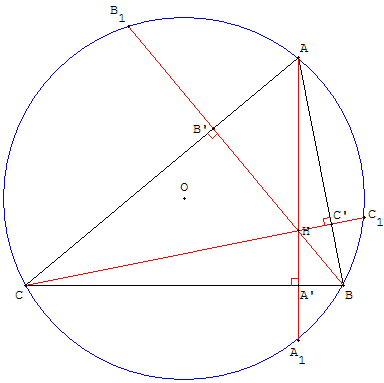
Relations métriques pour l'orthocentre d'un triangle

La puissance du point H par rapport au cercle circonscrit est :
HA × HA₁ = HB × HB₁ = HC × HC₁.

Sachant que les symétriques de l'orthocentre par rapport aux côtés du triangle
sont situés sur le cercle circonscrit au triangle (voir droite d'Euler) on a :
HA₁ = 2HA’, HB₁ = 2HB’, HC₁ = 2HC’;

On trouve donc :
HA × HA’ = HB × HB’ = HC × HC’.

3. Application de la théorie de l'axe radical

Construire un point défini par une relation métrique

On donne quatre points distincts A, B, C, D sur une droite (Δ).
Existe-t-il sur (Δ) un point I tel que . = ..

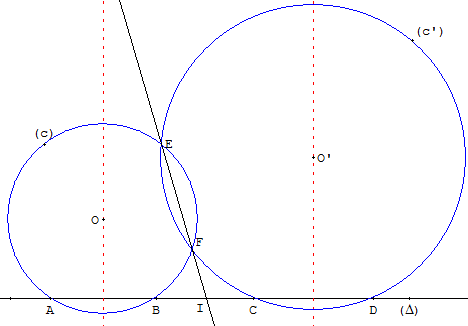
Si [AB] et [CD] n'ont pas même milieu,
on peut tracer un cercle (c) passant par A et B
et un cercle (c’) passant par C et D et coupant (c) en deux points E et F.

(EF) est l'axe radical de (c) et (c’).

Il rencontre (Δ) au point I cherché.

4. Différence des puissances d'un point pour deux cercles

Formule d'usage fréquent en géométrie du cercle,
qu'il faut savoir appliquer sans faute de signe.

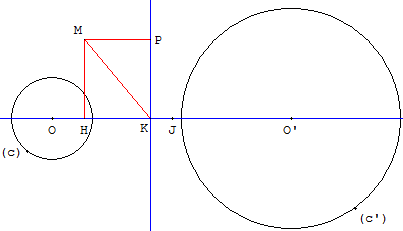
On considère deux cercles c(O, r) et c’(O’,r’) avec O et O’ distincts.
On note c(M) = MO² – r² la puissance de M par rapport à (c)
et c’(M) = MO’² – r^’2 la puissance de M par rapport à (c’).

c(M) – c’(M) = MO² – MO’² – (r² –r^’2).

En employant les carrés scalaires
MO² – MO’² = ² – ’² = ( + ’).( - ’)
      = 2 .( + ) = 2 ., avec J le milieu de [OO’].

Soit K le pied de l'axe radical des deux cercles. On a vu que :
2 . = r² – r’².

Donc
c(M) – c’(M) = 2 . – 2 . = 2 . + 2 . = 2 ..

Soit H la projection de M sur (OO’).

c(M) – c’(M) = 2 .    (1)

5. Relation d'Euler

Distance entre les centres des cercles inscrit et circonscrit

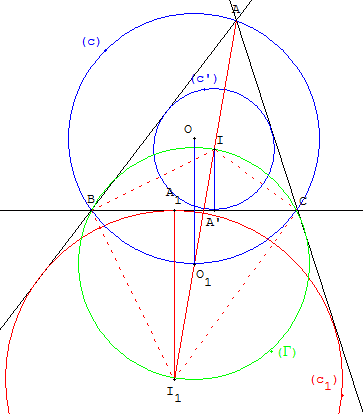
Si le cercle circonscrit (c) d'un triangle ABC a pour centre O et pour rayon R
et le cercle inscrit (c’) a pour centre I et pour rayon r.
Le rayon du cercle inscrit est  r = = .

La relation d'Euler permet de calculer le carré de la distance des deux centres :

OI² = R² – 2Rr.

Pour un cercle exinscrit (c₁) le centre I₁, intersection de la bissectrice
intérieure issue de A et de deux bissectrices extérieures issues de B et C,
est le barycentre de (A, -a) ; (B, b) ; (C, c).

Le rayon est r₁ = = = .

La relation d'Euler devient  :

OI₁² = R² + 2Rr₁.

Figure interactive dans GeoGebraTube :
       
cercles inscrit et exinscrit du triangle

Démonstration

Avec la puissance du point I par rapport aux cercles (c) et (Γ).

La bissectrice de l'angle BAC recoupe le cercle circonscrit en O₁,
milieu de l'arc BC, qui ne contient pas A.
Le cercle inscrit (c’) a son son centre I situé sur la bissectrice (AO₁)
et est tangent au côté (BC) en A’.
Le cercle (c₁), exinscrit dans l'angle A, de rayon r₁, a son son centre I₁
situé sur la bissectrice (AO₁) et est tangent au côté (BC) en A₁.
Les bissectrices intérieure (BI) et extérieure (BI₁)
sont perpendiculaires, ainsi que (CI) et (CI₁).
Le cercle (Γ) de diamètre [II₁] passe donc par B et C.
Il a son centre situé sur la bissectrice (II₁)
et sur la médiatrice de [BC]. C'est le point O₁.

Appliquons la formule (1) au point I et aux cercles (Γ) et (c) :
Γ(I) – c(I) = – 2 OO₁. A’I = – 2 Rr,
car les vecteurs OO₁ et A’I sont de sens contraires.

Comme Γ(I) = 0 et c(I) = IO² – R², on a bien OI² = R² – 2Rr.

De même, en appliquant la formule (1)
au point I₁ et aux cercles (Γ) et (c), on trouve :
Γ(I₁) – c(I₁) = 2 OO₁ × A₁I₁ = 2 Rr₁,
car les vecteurs OO₁ et A₁I₁ sont de même sens, d'où OI₁² = R² + 2Rr₁.

Voir : quatre relations d'Euler

6. Premier théorème de la médiane

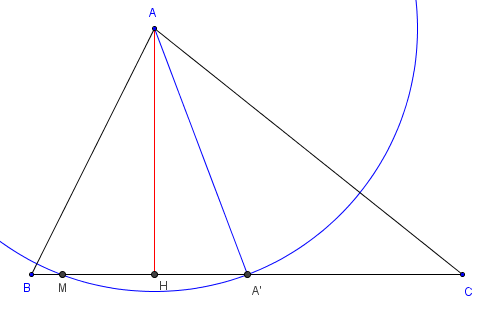
Soit un triangle ABC et le cercle de centre A passant
par le milieu A’ de [BC] et recoupant (BC) en M.

La puissance φ(B) de B par rapport au cercle de rayon AA’ est

φ(B) = AB² – AA’² = ×

et la puissance de C est φ(C) = AC² – AA’² = × .

Alors AB² + AC² – 2 AA’² = × + × .
     = ( – ) puisque = – ,

soit AB² + AC² – 2 AA’² = ( + ) = × = .

AB² + AC² = 2AA’² +
(formule d'Apollonius de Perge − premier théorème de la médiane).

Figure interactive dans GeoGebraTube : médiane et puissance d'un point

Triangle rectangle : où l'on retrouve Pythagore

Si le triangle est rectangle en A, alors A est sur le cercle de diamètre [BC]
et AA’ = BA’ = BC/2.

La formule d'Apollonius devient
AB² + AC² = 2(BC/2)² + = BC².

Différence des carrés des longueurs de deux côtés

φ(B) = AB² – AA’² = × ,
φ(C) = AC² – AA’² = × .

φ(B) – φ(C) = AB² – AC² = ( + ).

Introduisons H milieu de [MA’]. H est le milieu d'une
corde et [AH], hauteur du triangle ABC, est orthogonal à (BC).

AB² – AC² = ( + ) = ( + + + )
    = (2 ) = (4 ) = (4 ).

AB² – AC² = 2 .

Triangle rectangle : où l'on retrouve Pythagore

Si le triangle est rectangle en C, alors C et H sont confondus

= et AB² – AC² = 2 = BC².

Où l'on constate que le théorème de Pythagore n'est pas seule affaire
d'aires équivalentes et que l'ordre traditionnel des théorèmes
tel qu'il est étudié peut être perturbé.

Voir aussi : l'enseignement de la géométrie au Capes

Table des matières

Dans d'autres pages du site

Le cercle au collège

Le cercle au lycée

Cercles tangents à des droites ou à des cercles :
problèmes de contact, voir construction de cercles

Cercles tangents, tangents aux côtés d'un triangle

Triangle rectangle et cercles tangents

Droites de Steiner

Construction de Wallis

Google friendly ; sur ordinateur : cette page pour grand écran

Page n^o 149, réalisée le 31/7/2009
adaptée aux mobiles le 26/11/2015