Descartes et les Mathématiques

Calcul d'aires de pentagones par découpage

Figures réalisées avec un logiciel de géométrie dynamique.

Sommaire

1. Transformation d'un quadrilatère en un triangle

2. Transformation d'un polygone convexe en triangle

3. Aire d'un pentagone convexe

4. Aire d'un pentagone régulier

Autres aires : octogone, couronne

5. Carrés et octogone construits à l'intérieur d'un carré

6. Couronne

Les méthodes de découpages et recollement de figures pour
des calculs d'aires peuvent être considérées comme des
démonstrations mathématiques : le découpage et le recollement
correspondent à l'application d'un déplacement ou d'un
antidéplacement et ces deux types d'applications du plan
dans le plan conservent les aires.

Avec les élèves, on peut considérer que l'on a démontré
si l'on vérifie qu'il y a bien « recollement ».

1. Transformer un quadrilatère en triangle

Félix Klein - Problèmes célèbres de la géométrie élémentaire

Classe de 3^e

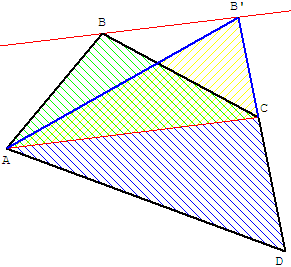
Transformation d'un quadrilatère convexe
ABCD en triangle AB’D de même aire.

On sait transformer le triangle ABC en AB’C où B’ est l'intersection
du côté (CD) et de la parallèle à la diagonale (AC) passant par B.

Par la propriété du trapèze, le triangle ABC a même aire que le triangle AB’C.

En ajoutant l'aire de ACD, le quadrilatère ABCD a même aire que le triangle AB’D.

2. Transformer un polygone en triangle

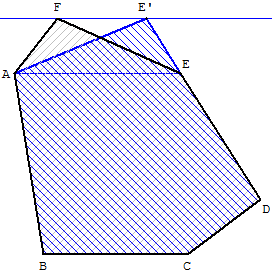
Transformation d'un polygone convexe en un triangle de même aire

Il est toujours possible de transformer un polygone
convexe de n côtés (n > 3) en un polygone
de n − 1 côtés de même aire.
Procéder comme ci-dessus en isolant quatre
sommets consécutifs ABCD.
Le polygone transformé ayant pour côtés
consécutifs AB’D a un côté de moins et l'aire est conservée.

Aire d'un hexagone : transformation d'un hexagone en pentagone

La parallèle à (AE) passant par F coupe (DE) en E’.
Par la propriété du trapèze, le triangle AEE’ a même aire que AEF.
Le pentagone ABCDE’ a même aire que l'hexagone ABCDEF.

Aire d'un pentagone : transformation d'un pentagone en quadrilatère

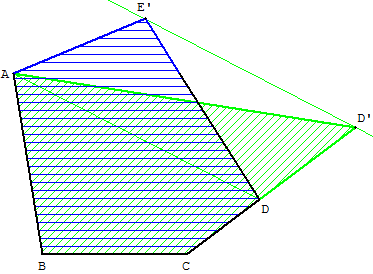
La parallèle à (AD) passant par E’ coupe (CD) en D’.
Le triangle ADD’ a même aire que ADE’.
Le quadrilatère ABCD’ a même aire que le pentagone ABCDE’.

Voir : calculer l'aire d'un hexagone régulier

Aire d'un quadrilatère : transformation d'un quadrilatère en triangle

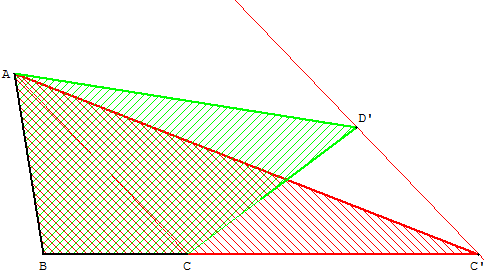
Comme ci-dessus, la parallèle à (AC) passant par D’ coupe (DE) en E’.
Par la propriété du trapèze, le triangle ACC’ a même aire que ACD’.
Le triangle ABC’ a même aire que quadrilatère ABCD’.

Surface d'un hexagone

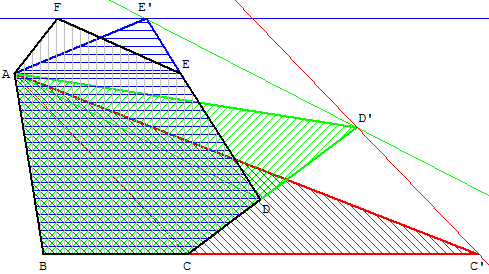
L'hexagone ABCDEF a même aire que le triangle ABC’.

L'hexagone ABCDEF, le pentagone ABCDE’,
le quadrilatère ABCD’ ont même aire que le triangle ABC’.

En utilisant la construction du rectangle de même aire que le triangle ABC’,
il est possible de changer l'hexagone en rectangle ;
voir transformer l'hexagone en carré avec la quadrature du rectangle.

3. Aire d'un pentagone (papillons)

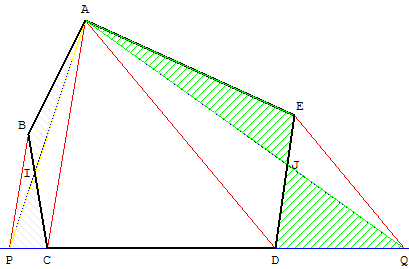
Transformation du pentagone convexe ABCDE
en un triangle APQ en utilisant deux fois
le théorème du papillon.

ABCDE est un pentagone (convexe).
Les parallèles aux diagonales AC et AD coupent la droite (CD) en P et Q.

L'aire du pentagone est égale à l'aire du triangle APQ.

Indications : l'aire du pentagone est égale à la
somme des aires des trois triangles ABC, ACD et ADE.

Solution : les triangles ABC et APC ont même base AC
et même hauteur égale à la distance entre les droites (AC) et (PC) ;
ils ont donc même aire.
De même, les triangles ADE et ADQ ont même aire.
L'aire du pentagone est alors égale à la somme des aires
des trois triangles APC, ACD et ADQ : c'est l'aire du triangle APQ.

Remarque : Il a été enlevé du pentagone les triangles ABI et AEJ,
que l'on a remplacés par les triangles CPI et DQJ d'aires équivalentes
(théorème du papillon).

4. Aire d'un pentagone régulier

4.a. Transformation de la surface du pentagone en triangle

Classe de troisième

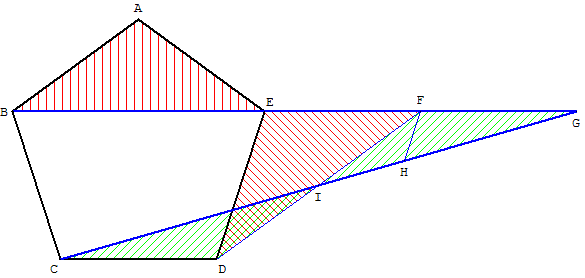
Dans le cas du pentagone régulier ABCDE,
il existe un découpage en quatre pièces.

En déplaçant le triangle ABE en EDF, on obtient
un trapèze BCDF d'aire équivalente à celle du pentagone.

Par symétrie par rapport au milieu I de [DF]
on remplace le triangle CDI par GFI.

L'aire du pentagone est égale à l'aire du triangle BCG.

Pentagone régulier :
    constructions exactes
    constructions approchées

4.b. Transformation d'un pentagone en parallélogramme

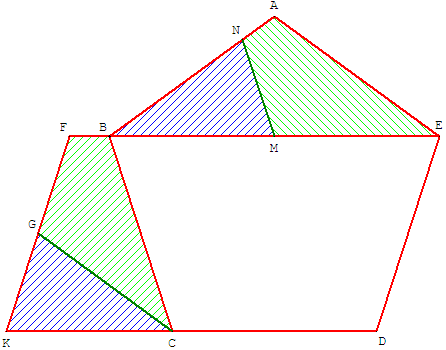
M est le milieu de la diagonale [BE].

Le triangle BMN est isocèle (triangle d'or d'angles 36° et 72°).

Avec ce puzzle de trois pièces, à partir du pentagone ABCDE,
il est possible de reconstituer un parallélogramme EFKD.

4.c. Transformation d'un pentagone régulier en carré

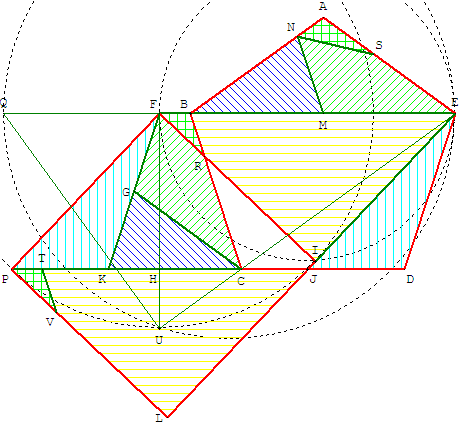
Reprenons la figure pour transformer le parallélogramme DEFK en carré.

En choisissant un point I sur le demi-cercle de diamètre [FE],
nous pouvons découper le triangle FEI et le translater en PJL,
avec un sommet en J, intersection de (EI) avec (CD).
[FI] et [IL] sont les côtés d'un carré de même aire que celle du pentagone.

4.d. Quadrature du pentagone

Côté du carré de même aire

Pour tracer un carré, nous utiliserons la méthode de la moyenne proportionnelle :
l'aire du parallélogramme DEFK est égale au produit de base FE par la hauteur FH.
Pour cette hauteur, rabattre le point H en Q sur (FE).
La droite (FH) coupe le cercle de diamètre (QE) en U.

Dans le triangle rectangle QEU, le carré de la hauteur FU issue de l'angle droit U
est égal au produit des segments QF et FE découpés sur l'hypoténuse
(Construction d'Euclide reprise par Descartes).

Le cercle de centre F passant par U coupe le cercle de diamètre [FE] en I.
Le quadrilatère BEIR est translaté en BJLV. Le triangle EJD est translaté en FPK.

Les six pièces du pentagone permettent de reconstituer un carré de même aire.

Remarques : FH est aussi la distance de F à la droite (MN).
Le point C n'est pas sur la droite (EU),
mais utiliser ce point est une erreur imperceptible.

5. Parallélogrammes et octogone dans un parallélogramme

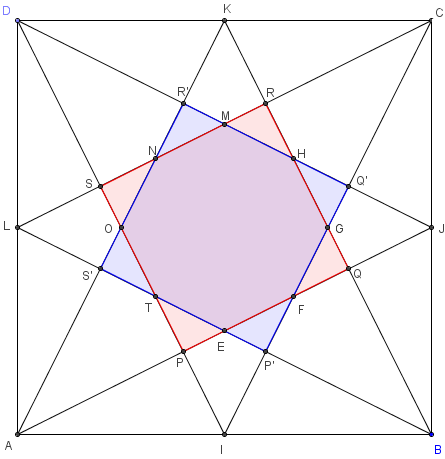
Soit ABCD un parallélogramme et I, J, K et L les milieux des côtés.

On trace les segments joignant les sommets aux milieux des autres côtés.
Au centre apparaissent parallélogrammes et octogone.
Quelle fraction de l'aire du parallélogramme
représente l'aire de ces polygones centraux ?

Cette propriété étant affine, on peut déplacer les sommets B et D
pour transformer ABCD en un carré, ce qui permet de faciliter les conclusions.

Deux carrés d'aire cinq fois plus petite…

PQRS est un carré d'aire 5 fois plus petite que l'aire du carré ABCD.
P’Q’R’S’ est aussi un carré de même aire.

Figure interactive dans GeoGebraTube :
     deux carrés d'aire cinq fois plus petite

Voir découpage d'aires dans un carré

Octogone d'aire six fois plus petite…

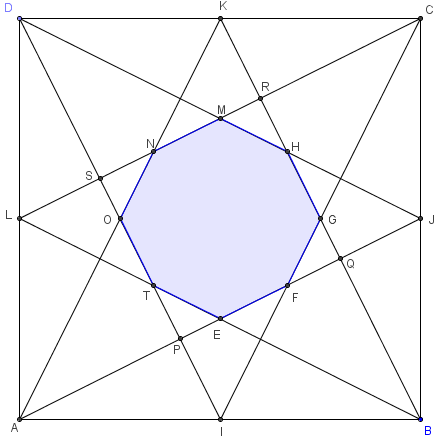
EFGHMNOT est un octogone d'aire 6 fois plus petite que l'aire du carré ABCD.

Remarque : les huit côtés de l'octogone sont de même longueur,
mais les angles ne sont pas égaux à 135°. L'octogone n'est pas régulier.

Figure interactive dans GeoGebraTube : octogone dans un carré

Voir octogone régulier

Indications

Comparaison, dans un quadrillage,
des aires du carré et de l'octogone

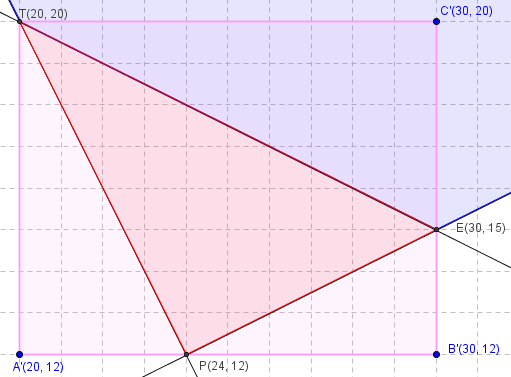
Les logiciels de géométrie dynamique font les calculs d'aire,
qui sont facilités en choisissant un côté du carré de longueur 60,
avec les sommets de coordonnées A(0, 0) ; B(60, 0) et D(0, 60).

Le carré ABCD a alors pour aire 60² = 3 600.
Les carrés centraux PQRS et P’Q’R’S’ ont pour aire 3 600/5 = 720.

Le logiciel trouve 30 pour l'aire du triangle PET,
soit un cent vingtième de l'aire du carré.

On peut le vérifier avec le quadrillage :
le triangle PET y est inscrit dans un rectangle A’B’C’T d'aire
A(A’B’C’T) = 10 × 8 = 80.

Les aires des triangles bordant PET sont :
A(A’PT) = 16, A(PB’E) = 9 et A(EC’T) = 25.

D'où
A(PET) = A(A’B’C’T) – A(APT) – A(PB’E) – A(EC’T)
          = 80 – 16 – 9 – 25 = 30.

L'aire de l'octogone est celle du carré PQRS diminué
quatre fois l'aire des triangles complémentaires :
720 – 4 × 30 = 600.

L'aire de l'octogone est six fois plus
petite que l'aire du carré ABCD.

6. Aire d'une couronne

Calcul de la surface d'une couronne
avec une corde tangente au petit cercle

Niveau 4^e − 3^e

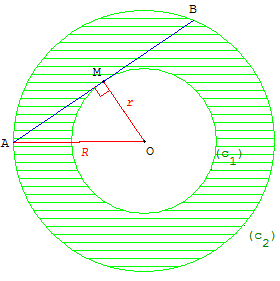
L'aire s d'une couronne est la différence entre
l'aire πR² du grand cercle et πr² celle du petit cercle :
s = πR² − πr² = π(R² − r²).

Problème : calcul sans connaître les rayons

Dans la figure, on ne connaît pas les rayons
r = OM et R  = OA des cercles (c₁) et (c₂) de centre O.
On sait seulement que la corde [AB] mesure a = 3 cm
et qu'elle est tangente au cercle intérieur (c₁).

On demande cependant de trouver l'aire s de la
couronne circulaire comprise entre (c₁) et (c₂).

Indications : la tangente (AB) au cercle (c₁)
en M est perpendiculaire au rayon [OM].
Le triangle AMO est rectangle en M d'où la
propriété de Pythagore AO² = AM² + MO²,
soit R² = (a)² + r² ou R² − r² = a².
L'aire s de la couronne est s = πR² − πr² = π(R² − r²) = a²,
expression de l'aire de la couronne uniquement en fonction de a.

Cas particulier :

Corde égale au diamètre du petit cercle

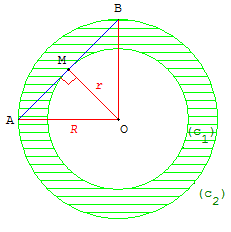
Si AB est égal au diamètre du cercle (c₁), r = a,
alors le triangle AMO est rectangle isocèle et R = r ;
le triangle AOB est aussi rectangle isocèle.

L'aire du cercle (c₂) est double de celle de (c₁),
l'aire de la couronne πr² est alors égale à l'aire du cercle intérieur.

Table des matières

Dans d'autres pages du site

Index aires

Aires et triangles

Aires du parallélogramme, du losange et du trapèze

Lunule

Google friendly ; sur ordinateur : cette page en grand écran