Descartes et les Mathématiques

Polygone régulier

Comment tracer les polygones réguliers de 5 à 17 côtés.

Sommaire

1. Polygone régulier : définition ; côtés, angles

2. Polygone régulier constructible

5. Pentagone - Construction de Ptolémée

6. Hexagone

7. Heptagone

8. Octogone

9. Ennéagone

10. Décagone

12. Dodécagone

15. Pentédécagone

17. Heptadécagone (construction de Gauss)

1. Polygones réguliers : définition ; côtés, angles

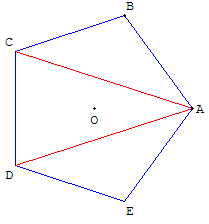
Un polygone régulier est un
polygone inscrit dans un cercle
et dont tous les côtés ont la
même longueur et tout les
angles la même mesure.

Un polygone régulier est
soit un polygone convexe,
soit un polygone étoilé.

Tous les polygones réguliers
convexes d'un même nombre
de côtés sont semblables.

Un polygone régulier à n côtés se superpose à lui-même
quand on le tourne d'un angle de .

Un polygone régulier est composé de (n − 2) triangles.
Si on additionne les angles de ces triangles, on obtient
la somme des angles intérieurs du polygone.

La somme des angles d'un polygone à n côtés est égale :
(n − 2) × 180° (Scholie de la proposition 32 du livre I d'Euclide :
somme des angles d'un triangle).

Les rayons d'un polygone inscrit dans un cercle, de rayon r,
relient ses sommets à son centre.
Les apothèmes relient les milieux de ses côtés à son centre.

2.a. Polygone constructible

Savoir construire un polygone régulier, à n côtés,
c'est savoir tracer le point de coordonnées (cos, sin ).
Ayant ainsi construit un côté de ce polygone, il suffit de
reporter de proche en proche sa longueur sur le cercle unité.

Les Éléments d'Euclide donnent les constructions des
polygones réguliers de 3, 4, 5, 6 et 15 côtés.
Ils expliquent comment, grâce à la construction des
bissectrices, doubler le nombre de côtés d'un polygone.

2.b.Théorème de Gauss

Soit n et m deux entiers naturels premiers entre eux. Le
polygone à nm côtés est onstructible à la « règle et au
compas » si et seulement si les polygones à n côtés et
à m côtés sont constructibles.

En effet, l'identité de Bézout permet de dire que si m et n
sont premiers entre eux,
il existe deux entiers relatifs u et v tels que um + vn = 1.
Multipliant cette expression par ,
il vient : u + v = .

On obtient l'angle , sur le cercle unité, en reportant
u fois l'angle et v fois l'angle , angles que l'on sait construire.

Exemple - construction du polygone régulier à 15 côtés :
Comme on sait tracer le triangle équilatéral et le pentagone
régulier, 3 et 5 étant premiers entre eux, en multipliant
par la relation de Bézout 2 × 3 − 5 = 1,
on obtient l'égalité 2 − = .
Sur un cercle, à partir d'un point A, on place un point G tel
que (, ) = , le point B tel que (, ) = − est le
deuxième sommet du polygone régulier de côté AB.

Il faudra attendre 1796 pour que Gauss démontre que le
polygone de 17 côtés était aussi constructible à la « règle et au compas ».

2.c. Polygones constructibles

Un polygone régulier de n côtés est constructible si cos est
un nombre constructible. n est alors une puissance de 2,
un nombre premier de Fermat de la forme 1 + 2^(2k), un produit
de nombres de Fermat ou un produit d'une puissance de 2 par
des nombres de Fermat.

Pour n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20…
les polygones à n côtés sont constructibles.

Pour n = 7,   9, 11, 13, 14, 18, 19… ils ne le sont pas.

5. Dessiner un pentagone régulier

Construction de Ptolémée du pentagone régulier

Classe de troisième

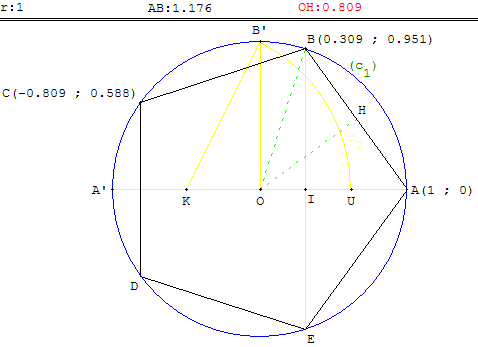
Pour dessiner un pentagone régulier convexe inscrit dans un
cercle, à la « règle et au compas », il suffit de savoir
construire un angle au centre de 72° dont le cosinus est égal à .

Pour un pentagone inscrit dans un cercle de centre O, ayant un
sommet A donné on peut effectuer la construction adaptée du
procédé de création du rectangle d'or :

tracer un cercle (c₁) de centre O, de rayon r, passant par A(r, 0).
Placer un diamètre [AA’], puis un rayon [OB’], perpendiculaire à [AA’].

K est le milieu de [OA’], le cercle (c₂) de centre K et de rayon KB’
coupe [OA] en U. La longueur du côté du pentagone est égale à B’U.

La médiatrice de [OU] coupe le premier cercle (c₁) aux points B et E
qui sont deux sommets du pentagone. Le cercle de centre B passant
par A recoupe (c₁) en C. Le symétrique D de C par rapport à (AA’)
termine la construction du pentagone.

En effet, KB’ = KU = r d'après la propriété de Pythagore,
dans le triangle OKB’ rectangle en O,
donc OU = r( − ) = et OI =  r.
L'angle (, ) a un cosinus égal à , c'est bien un angle
de 72°. La corde [AB] est donc le premier côté du pentagone
régulier convexe ABCDE.

Le point B a pour coordonnées OI = r cos 72°
et IB = r sin 72°.
Le point C a pour abscisse
r cos 108° = − r cos 72° = − r ;
et pour ordonnée r sin 108° = r sin 72°.

Figure interactive dans GeoGebraTube : pentagone régulier

   Feuille interactive avec GeoGebra : pentagone

Tracer un pentagramme

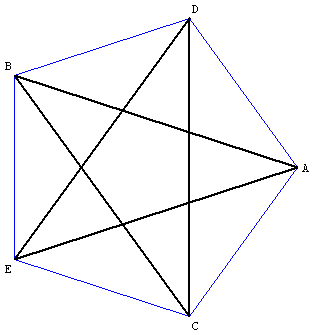
On obtient un pentagone étoilé en joignant, de deux en deux,
les sommets d'un pentagone régulier.

Le pentagone croisé ABCDE est obtenu à partir
du pentagone convexe ADBEC.

Figure interactive dans GeoGebraTube : pentagramme étoilé

Figure exportée dans WikiPédia : pentagone étoilé, pentagramme

Côtés des pentagones convexe ou étoilé

Calculer les longueurs des côtés des pentagones réguliers convexe ou étoilé

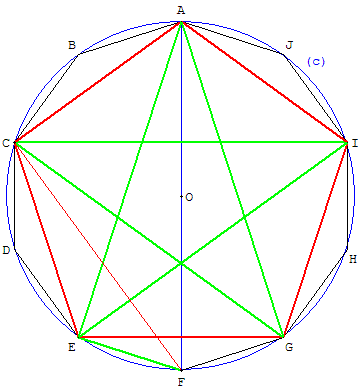
On inscrit dans un cercle (c) de centre O et de rayon r
un décagone régulier. En joignant les sommets, de deux en deux,
on obtient un pentagone régulier convexe ACEGI ; en les
joignant de quatre en quatre on obtient un pentagone régulier
étoilé AEICG (pentagramme).

Soit a = AC la longueur du côté du pentagone, d = AE
la longueur d'une diagonale, côté du pentagone étoilé.

Le triangle isocèle AEG, d'angle au sommet 36°, est un triangle d'or.
Le rapport entre le côté AE du triangle et sa base EG est le nombre d'or φ.

Côtés des pentagones convexe et croisé ; décagone

Dans le pentagone le rapport est
= = φ = :
d = a φ.

La longueur du côté du décagone régulier est
EF = = r ,
en joignant les sommets de trois en trois, la longueur du côté
du décagone croisé est :
CF = r φ = r .

Les relations de Pythagore dans les triangles rectangles ACF
et AEF inscrits dans le demi-cercle de diamètre [AF] donnent :
a² = AC² = AF² − CF² = 4r² − r²φ²
et d² = AE² = AF² − EF² = 4r² − r²/φ².

On trouve alors :
Côté du pentagone régulier :
a = 2 r sin 36° = = r ≈ 1,176 r ;
Côté du pentagone croisé :
d = = r ≈ 1,902 r.

Pentagone régulier :
    constructions exactes
    constructions approchées

6. Hexagone

Comment tracer un hexagone régulier à partir d'un cercle

Classe de quatrième

L'hexagone régulier est inscrit dans un cercle dont le rayon r
est égal à la longueur des côtés de l'hexagone.

6.a. Construction de l'hexagone à partir du cercle circonscrit

Euclide

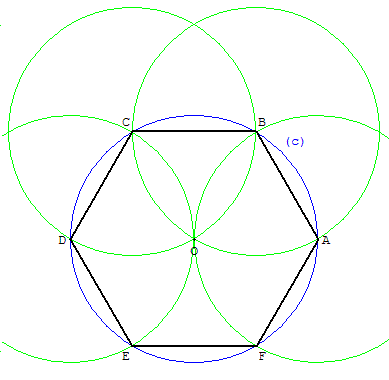
Comment tracer un hexagone:
Pour dessiner un hexagone régulier inscrit dans un cercle,
il suffit de porter six fois sur la circonférence une ouverture
de compas égale au rayon et de joindre les points consécutifs
ainsi obtenus.

Géométrie dynamique

Placer deux points O et A,
tracer le cercle (c) de centre O, passant par A.

Le cercle de centre A, passant par O, coupe le cercle (c) en B et F,
le cercle de centre B, passant par O, recoupe le cercle (c) en C,
le cercle de centre C passant par O coupe le cercle (c) en D,
le cercle de centre D passant par O coupe le cercle (c) en E.

Effacer les cercles et tracer les côtés de l'hexagone ABCDEF.

Voir : construction d'un hexagone par pliage d'un triangle équilatéral

construction en partageant le diamètre d'un cercle en quatre

6.b. Hexagone à partir d'un côté

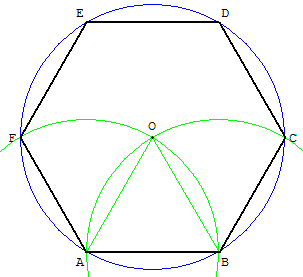
Étant donné un segment [AB], tracer les cercles de
centre A passant par B et de centre B passant par A.

O, un des points d'intersection de ces deux cercles,
est le centre du cercle circonscrit l'hexagone.

La construction se termine comme ci-dessus.

6.c. Hexagone à partir du cercle inscrit

Classe de première L

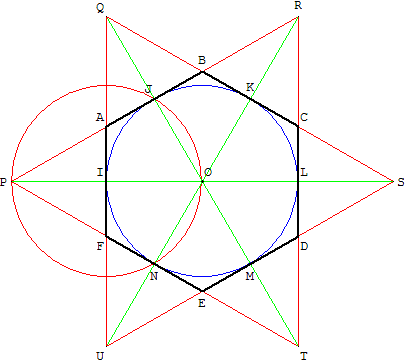
Étant donné deux points O et I, tracer l'hexagone passant par I,
circonscrit au cercle (c) de centre O, passant par I.

Tracer le cercle de centre I, passant par O. Soit J et N les points
d'intersection de ce cercle avec le cercle (c). Soit P le symétrique
de O par rapport à I. Le triangle PJN est équilatéral. (PJ) est
perpendiculaire au rayon [JO] de (c). (PJ) est tangente
au cercle (c). (PN) est aussi une tangente.

Soit R et T les symétriques de P par rapport à J et à N. PRT
est un triangle équilatéral dont les côtés sont tangents au cercle (c).

Le cercle (c) est aussi inscrit dans le triangle équilatéral SUQ,
symétrique de PRT par rapport à O.

Les six points d'intersection de ces deux triangles forment
l'hexagone ABCDEF, circonscrit au cercle (c).

6.d. Hexagramme étoilé

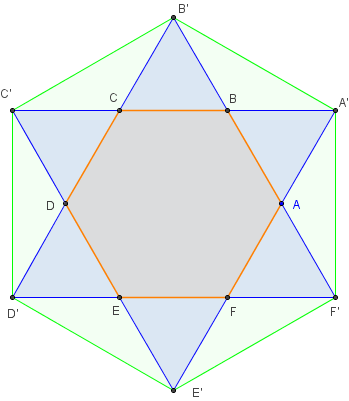
L'hexagone régulier ABCDEF, inscrit dans le cercle circonscrit
de centre O et de rayon r, est composé de 6 triangles équilatéraux
de côtés r, d'aire s.
L'aire de l'hexagone est S = 6s.

En prolongeant les côtés de l'hexagone, on trouve
six points d'intersection A', B', C'...
On obtient six pointes, triangles équilatéraux de cotés r.
L'étoile de David AA'BB'CC'DD'EE'FF' est formée de
l'hexagone et des 6 pointes.
Son aire, réunion de 12 triangles équilatéraux, est 12 s = 2S,
soit le double de l'aire de l'hexagone.

L'hexagramme A'B'C'D'E'F' est un hexagone régulier obtenu en
complétant l'étoile par six triangles isocèles de petits côtés r
et d'angle 120°.
Par exemple, les triangles A'BB' et BCB' ont même base r et
même hauteur, celle du triangle équilatéral, ils ont donc même aire s.
La somme des aires des triangles isocèles est 6s = S.
A'B'C'D'E'F a pour aire 2S + S = 3S.
Le rapport d'agrandissement des hexagones est donc .

Figure interactive dans GeoGebraTube : hexagramme étoilé

Hexagramme mystique

6.e. Calculer l'aire d'un hexagone régulier

La longueur r des côtés de l'hexagone est égale au rayon du cercle circonscrit.
L'hexagone régulier est composé de six triangles équilatéraux.

Chaque triangle équilatéral de côté r, a pour aire r².

Formule de l'aire de l'hexagone régulier :

l'aire de l'hexagone régulier de côté r est : r².

7. Heptagone

Le seul texte d'origine grecque dont on ait trace sur une construction exacte
de l'heptagone régulier est attribué à Archimède :
Sur la division d'un cercle en sept parties égales.

Construction approchée, dite « de Thalès »

L'heptagone est le premier polygone régulier à n'être pas constructible
à la « règle et au compas ».

En effet, pour a = , calculons cos() grâce aux
cosinus des angles supplémentaires et :
cos(4a) = 8 cos⁴(a) − 8 cos²(a) + 1
et cos(3a) = 4 cos³(a) − 3 cos(a).

En remplaçant cos() par x,
dans l'égalité cos() = − cos();
on a : 8x⁴ − 8 x² + 1 = − 4 x³ + 3x
soit l'équation 8x⁴ + 4 x³ − 8 x² − 3x + 1 = 0.

L'angle a = π est aussi solution pour x = cos(π) = − 1.
On peut donc factoriser (x + 1)
soit (x + 1) (8x³ − 4x² − 4x + 1) = 0

cos() est donc solution
de l'équation 8x³ − 4x² − 4x + 1 = 0.

Équation irréductible dans Q

Soit une solution rationnelle irréductible de l'équation
8x³ − 4x² − 4x + 1 = 0.
Dans Z on a alors 8p³ − 4 p²q − 4 pq² + q³ = 0.

Il résulte du théorème de Gauss que p divise 1 et q divise 8.
Les candidats pour sont à chercher parmi les facteurs de .

Dans ce cas particulier,
de l'égalité 8p³ − 4 p²q − 4 pq²+ q³ = 0, il s'ensuit que q est pair.
Posons alors q = 2r. Il vient,
l'égalité : p³ − p²r − 2pr² + r³ = 0.

Mais la fraction étant irréductible p est premier avec q et par
suite avec sa moitié r. Du théorème de Gauss,
il résulte que p divise 1 et r divise 1.
Donc p = ±1 et r = ± 1, d'où q = ± 2.
En conséquence x = ± et on vérifie que ± n'est pas solution
de l'équation. L'équation n'a pas de solution dans Q.

Polynôme minimal du troisième degré

P(x) = 8x³ − 4x² − 4x + 1 admet comme solution cos().
Cette solution n'est pas rationnelle.

Soit un autre polynôme Q(x) de Q[X], de degré
moindre, qui aurait cos() comme 0.
Si Q(x) était un binôme de degré 1, il admettrait une
solution rationnelle ce qui n'est pas le cas.

Q(x) est donc du second degré.
Grâce à la division euclidienne de P(x) par Q(x),
on trouve P(x) = Q(x) (ax + b) + R(x),
avec a non nul et R(x) binôme du premier degré.

En remplaçant x par cos(), on trouve que R(cos()) = 0,
cette solution n'étant pas rationnelle, cette première
contradiction impose donc R(x) = 0.
P(x) alors égal à Q(x) (ax + b) serait factorisable dans
Q[X] et aurait − b/a pour solution ce qui est impossible.

cos() n'est pas solution d'une équation du second degré
à coefficients entiers. P(x) est irréductible dans Q[X].
cos() est algébrique sur Q de degré 3.

Le nombre cos() n'est pas constructible et, d'après le
théorème de Wantzel, il est impossible de tracer l'heptagone
régulier à la « règle et au compas ».

Voir aussi une démonstration montrant
si l'équation admet une solution constructive, elle admet une solution
rationnelle, d'où la contradiction.

Construction de Thalès

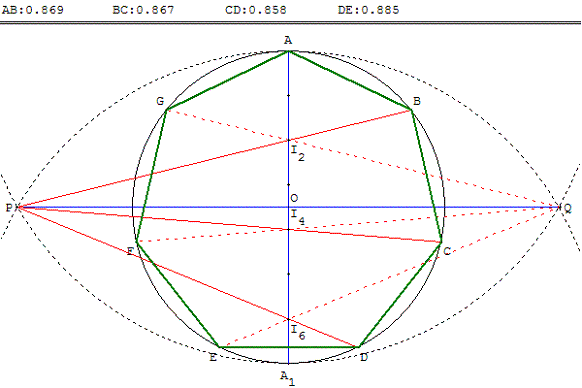
Cette construction d'un heptagone presque régulier est attribuée
au mathématicien et philosophe grec Thalès de Milet (vers 600
avant J.-C.). Elle nécessite la règle et deux ouvertures de compas.

Deux points A et A₁ étant donnés, tracer le cercle (c) de diamètre [AA₁].
Les cercles de centres A et A₁ et de rayon AA₁ se coupent en P et Q.

On divise le diamètre [AA₁] en n = 7 parties égales.

Les droites (PI₂), (PI₄) et (PI₆) rencontrent le cercle (c) en B, C et D,
sommets du polygone. On complète par symétrie par rapport à (AA₁).
On obtient les points G, F et E intersections du cercle (c)
et des droites (QI₂), (QI₄) et (QI₆).

ABCDEFG est une construction approchée de l'heptagone régulier.

Construction d'un polygone de n côtés

Cette méthode s'applique à un polygone de n côtés.
Elle est d'une grande facilité et d'une précision très
satisfaisante jusqu'à n = 10.

Voir une autre construction de l'heptagone :

Traité de géométrie pratique de Sébastion Leclerc

8. Dessiner un octogone régulier

Classe de troisième

En fonction du rayon r du cercle circonscrit, la longueur du côté est:
2 r sin = r ≈ 0,765 r.

Voir le calcul du sinus de 45° : angle trigonométrie

8.a. Octogone inscrit dans un cercle

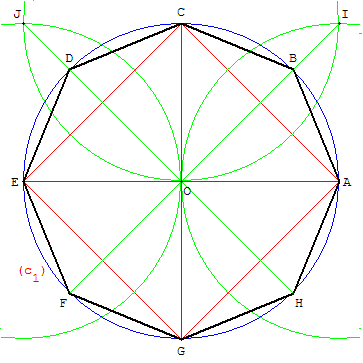
À partir de deux points O et A, tracer le cercle
de centre O, passant par A.
Tracer deux diamètres [AE] et [CG] perpendiculaires :
ACEG est un carré.

Tracer les bissectrices des angles formés
par les droites (AE) et (CG).

Pour cela, tracer les cercles de centres A et C,
passant par O, qui se recoupe en I.
(OI) est la médiatrice de [AC] et coupe le cercle en B et F.

Tracer les cercles de centres C et E, passant par O,
qui se recoupe en J.
(OJ) est la médiatrice de [CE] et coupe le cercle en D et H.

En joignant les extrémités de ces quatre diamètres,
on obtient l'octogone régulier ABCDEFGH.

Figure interactive dans GeoGebraTube : octogone

8.b. Octogone inscrit dans un carré

Dessiner un carré PQRS, de centre O.

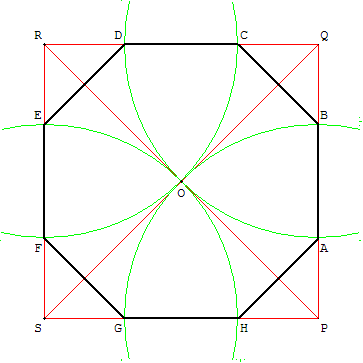
Tracer alternativement les cercles centrés sur chaque
sommet du carré, passant par le centre O.

En joignant les points d'intersection de ces cercle
avec les côtés du carré, on obtient un octogone
régulier inscrit dans un carré.

Figure interactive dans GeoGebraTube :
        octogone inscrit dans un carré

Voir : octogone non régulier construit à l'intérieur d'un carré

8.c. Points d'intersection de deux carrés

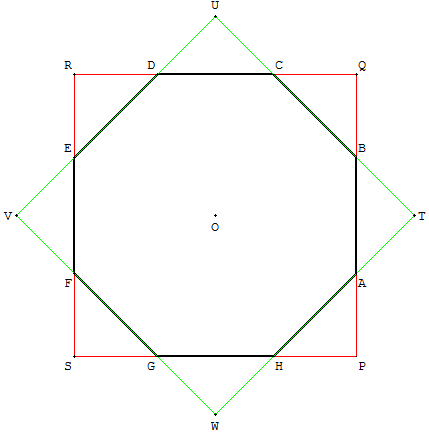
Sommets de l'octogone comme points
d'intersection de deux carrés

Tracer un carré PQRS a pour centre O.
Une rotation de centre O et d'angle 45°
transforme ce carré en TUVW.

Les points d'intersection de ces deux carrés
forment un octogone régulier.

8.d. Dessiner un octogone à partir d'un côté

Classe de première L

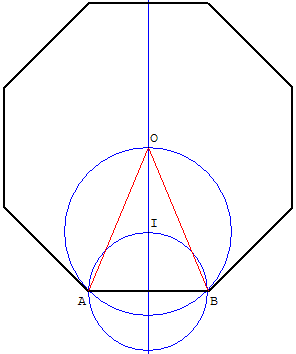
Comment dessiner un octogone régulier à partir d'un côté

Du centre O du cercle circonscrit,
on « voit » un côté [AB] suivant un angle de 45°.
Le point O est situé sur arc capable correspondant
à un angle au centre de 90°.
Le centre I de l'arc capable est donc situé sur le
cercle de diamètre le côté [AB].

Construction

Étant donné deux points A et B, tracer le cercle de diamètre
[AB], la médiatrice de [AB] coupe ce cercle en un point I.

Le cercle de centre I, passant par A, coupe la médiatrice en
un point O, situé du même côté que I, par rapport à (AB).

AÔB = AÎB = 45°, le point O est le centre du cercle
circonscrit à l'octogone.

On termine la construction comme ci-dessus à gauche.

Voir cette construction utilisée dans l'espace :
        pyramide octogonale

8.e. Octogone délimité par 4 triangles équilatéraux

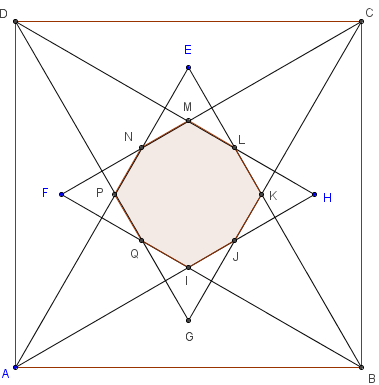
Quatre triangles équilatéraux construits à
l'intérieur d'un carré délimitent un octogone

À l'intérieur d'un carré ABCD, construire quatre
triangles équilatéraux ABE, BCF, CDG et DAH.

L'intérieur de cette figure forme un octogone régulier.

Figure interactive dans GeoGebraTube :
        octogone et triangles équilatéraux

Voir octogone (non régulier) à l'intérieur d'un carré,

Construction du pentagone régulier

8.f. Construction de l'octogone étoilé

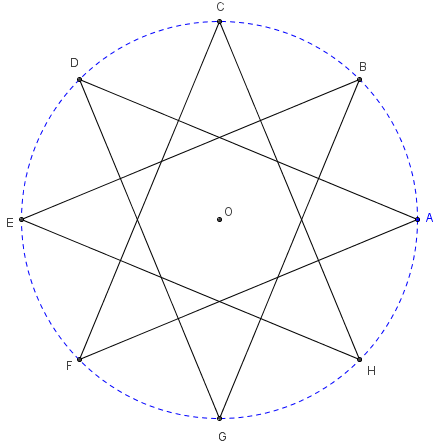
ABCDEFGH est un octogone régulier.
En joignant les sommets trois à trois,
on obtient l'octogone croisé ADGBBEHCF.

Figure interactive dans GeoGebraTube : octogone étoilé

9. Ennéagone

Non constructible à la « règle et au compas », car la
trisection d'un angle de mesure radians n'est pas possible,
résultat prouvé en 1801 par Gauss.

Page en projet : ennéagone

Construction approchée de Thalès

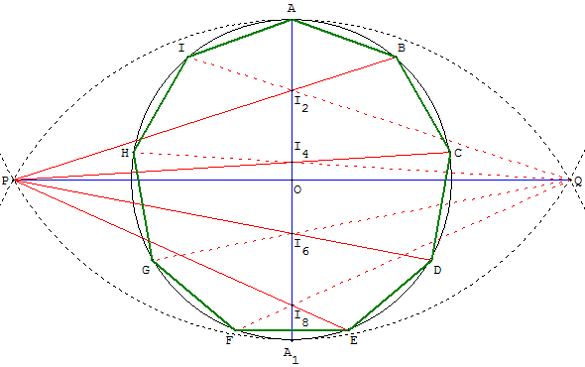
Deux points A et A₁ étant donnés, tracer le cercle (c)
de diamètre [AA₁].
Les cercles de centres A et A₁ et de rayon AA₁ se
coupent en P et Q.

On divise le diamètre [AA₁] en n = 9 parties égales.

Les droites (PI₂), (PI₄), (PI₆) et (PI₈) rencontrent le
cercle (c) en B, C, D et E, sommets du polygone.
On le complète par symétrie par rapport à (AA₁).

On obtient alors les points I, H, G et F intersection
du cercle (c) et des droites (QI₂), (QI₄), (QI₆) et (QI₈).

ABCDEFGHI est une construction approchée de l'ennéagone régulier.

10. Construire un décagone régulier

Le décagone se construit au compas par la dissection d'un pentagone.

10.a. Méthode des cercles tangents

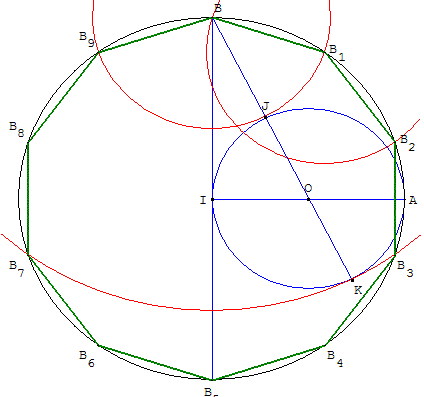
Dessiner un décagone avec la méthode des cercles tangents

Décagone BB₁B₂B₃B₄B₅B₆B₇B₈B₉, construit à partir du
sommet B, inscrit dans un cercle (c₂), de centre I et de rayon IA.

Construction

Construire un rayon [IA], perpendiculaire à (IB).

Tracer le cercle (c₁), de diamètre [IA], de centre O.
La droite (BO) rencontre le petit cercle (c₁) en J et K (BJ < BK).

Le cercle (c₃) de centre B, passant par J, rencontre le grand
cercle (c₂) en B₁ (et en B₉), sommets du décagone.
Reporter l'ouverture BB₁ sur le cercle en B₂, puis de B₂ en B₃, etc.

On peut continuer la construction des sommets du décagone
avec les symétries par rapport aux droites (IA) et (IB).
Les points B₃ et B₇ sont aussi situés sur le cercle
de centre B passant par K.

Voir pentagone : méthode des cercles tangents

Construction de Ptolémée du décagone

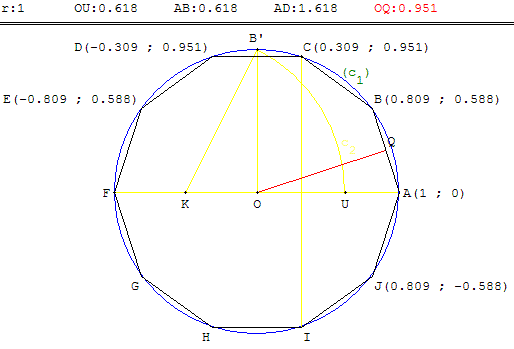
Construction du décagone régulier

Les cinq autres sommets, points d'intersection du cercle
circonscrit avec les bissectrices de rayons consécutifs
, sont les symétriques des sommets du pentagone par rapport au centre.
Tracer le pentagone ACEGI de centre O et son symétrique FHJBD.

ABCDEFGHIJ est un décagone régulier de côté :

AB = OU = r( − ) = .

10.c. Décagone et triangle d'or

[AB] est le côté du décagone ABCDEFGHIJ régulier convexe
inscrit dans un cercle (c) de centre O, [AD] est le côté du
décagone étoilé.

[AD] et le rayon [BO] se coupent en M. Le rayon (BO)
prolongé passe par le sommet G et le rayon (DO)
prolongé passe par le sommet I.

10.e. Décagone étoilé

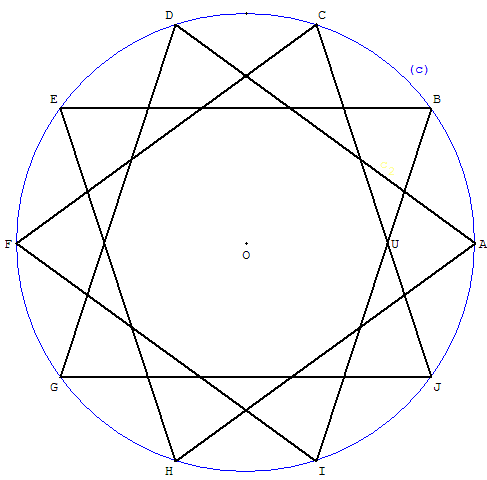
Le nombre de polygones réguliers croisés de n côtés est
égal au nombre de nombres premiers avec n contenus dans
la suite 2, 3…, . Comme pour le pentagone, il n'y a
qu'un décagone croisé que l'on obtient en joignant
les sommets de trois en trois.

Triangles d'or

OAB est un triangle isocèle de côtés égaux au rayon r du
cercle circonscrit. L'angle AÔB = 36° comme angle au centre
du décagone. Les deux autres angles mesurent 72° comme
angles inscrits interceptant quatre divisions sur le cercle (c).
OAB est donc un triangle d'or. Le rapport entre le côté
du triangle et sa base est φ.
Le côté du décagone est AB = .

L'angle inscrit IDA intercepte deux divisions, il mesure 36°.
L'angle au centre BÔD intercepte deux divisions, il mesure 72°.
DOM est donc un triangle d'or, isométrique à OAB. L'angle
OMD mesure 72°, ainsi que l'angle AMB, qui lui est opposé par
le sommet. L'angle inscrit BAD intercepte deux divisions,
il mesure 36°. ABM est encore un triangle d'or.

MOA a pour angles à la base deux angles inscrits de 36°,
il est donc isocèle : OM = AM = AB = .

AD = AM + MD = + r = rφ.

On peut aussi remarquer que l'angle de 36°, que fait la corde
[OM] avec [OA], est égal à l'angle ODM inscrit dans le cercle
circonscrit au triangle ODM. (OA) est tangent au cercle.
La puissance du point A par rapport à ce cercle est

AD × AM = AO².

Comme AM = AB on obtient les deux côtés en divisant
le rayon en « extrême et moyenne raison »

AB = = r et AD = r φ = r .

11. Hendécagone

Non constructible à la « règle et au compas ».

12. Dodécagone

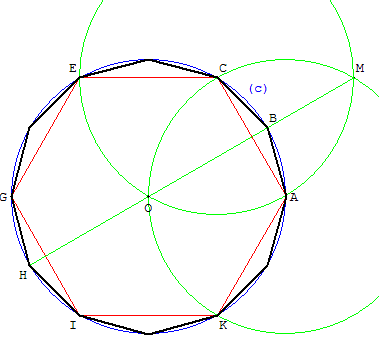
C'est un polygone à 12 sommets et côtés. Il possède 54
diagonales et la somme de ses angles est égale à 1800°.

Le dodécagone se construit au compas par la dissection d'un
hexagone : les six autres sommets sont les points d'intersection
du cercle circonscrit avec les bissectrices de rayons consécutifs.

12.a. Construction par dissection d'un hexagone

À partir d'un hexagone ACEGIK inscrit dans le cercle (c), on
utilise les cercles passants par O, centrés sur deux sommets
consécutifs, ayant permis la construction de l'hexagone.
Par exemple, les cercles de centres A et C passant par O se
recoupent en M. La droite (AM) est la médiatrice du côté [AC].
Elle coupe le cercle (c) en B et H qui sont deux sommets
opposés du dodécagone.

12.b. Construction au compas

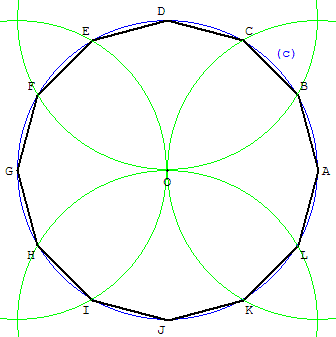
Dans le cercle (c), de centre O, tracer deux
diamètres [AG] et [DJ] perpendiculaires.

Les points du dodécagone sont les points d'intersection
du cercle (c) avec les cercles de centres A, D, G et J
passant par le centre O.

12.c. Aire du dodécagone

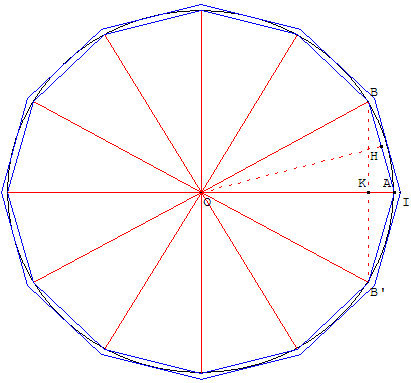
On choisit OA comme unité.
Un dodécagone régulier est inscrit dans le cercle (c) de centre O et de rayon 1.
On le partage en 12 triangles isocèles.

Dès la cinquième on peut, en remarquant que le triangle
isocèle OBB’ ayant un angle de 60° est équilatéral,
montrer que BB’ = 1.

La hauteur BK du triangle OAB est égale à et l'aire du
triangle est égale à .
Le dodécagone a donc une aire égale à 3.

Elle est inférieure à l'aire du cercle (c), d'où 3 < π.

Au lycée, en 1^ère S, on montrera que
OH = cos = .

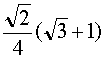Voir angle-trigonométrie

En choisissant OI = = on construit un
dodécagone tangent extérieurement au cercle (c)
d'aire : 3 OI² ≈ 3.22, donc 3 < π < 3,22.

12.d. Construction du dodécagone autour d'un hexagone

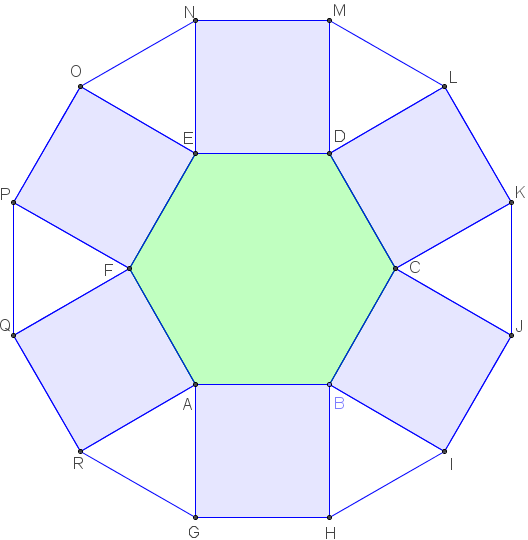
Sur chaque côté, de longueur a, d'un hexagone réguler,
à l'extérieur, on construit six carrés et joint les
sommets des carrés consécutifs.
On forme ainsi six triangles isocèles d'angles au
sommet 360° - 120° - 90° - 90° = 60°.
Ces six triangles sont donc équilatéraux.

La figure est formée de 12 côtés de longueur a, formant des
angles de 90° + 60° = 150° est un dodécagone régulier.

Aire en fonction du côté

L'hexagone est décomposable en six triangles équilatéraux
de côtés a d'aire a².
L'aire de l'hexagone est 3 a².

Les six triangles équilatéraux extérieurs ont aussi pour
aire :3 a² et l'aire des carrés est 6a².

L'aire du dodécagone est donc 3a²(2 + ).

L'apothème OH (rayon du cercle inscrit) est égale au coté
du carré, plus la hauteur d'un triangle équilatéral :

OH = a(1 + )

Figure interactive dans GeoGebraTube : dodécagone régulier

12.d. Avec quatre triangles équilatéraux

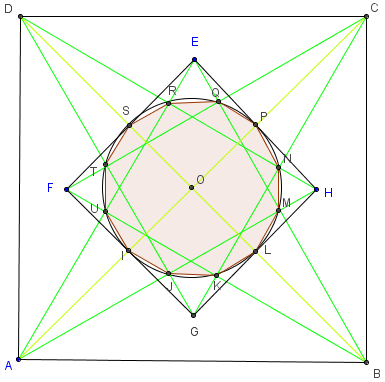
Dessiner un dodécagone avec quatre triangles équilatéraux

On reprend la construction de l'octogone délimité par quatre
triangles équilatéraux construits à l'intérieur d'un carré

À l'intérieur d'un carré ABCD, construire quatre triangles
équilatéraux ABE, BCF, CDG et DAH.
Les quatre sommets internes des triangles équilatéraux
forment un carré EFGH.

Le milieu des petits côtés et les intersections des côtés des
triangles proches des sommets forment un dodécagone régulier.

L'aire du dodécagone est égale au cinquième de l'aire du carré.

Figure interactive dans GeoGebraTube :
        dodécagone et triangles équilatéraux

15. Pentadécagone ou pentédécagone,

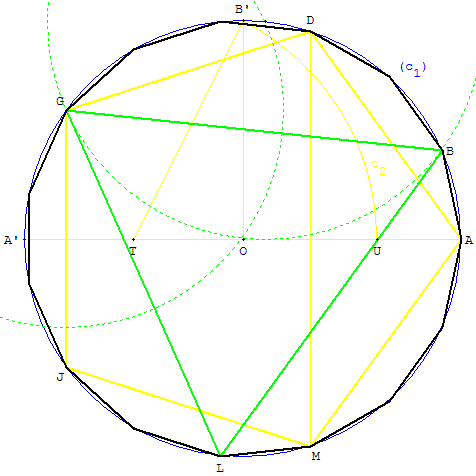
ou encore quindécagone

15.a. Découpage d'un arc grâce à un triangle
équilatéralet un pentagone inscrit dans un cercle.

Comme on sait construire le triangle équilatéral et
le pentagone régulier, on applique le théorème de Gauss :

3 et 5 étant premiers entre eux, en multipliant par
la relation de Bézout : 2 × 3 − 5 = 1,
on obtient l'égalité 2 − = ,
qui fournit une construction.

Sur un cercle, à partir d'un point A, on place un point G tel que :
(, ) = ,
le point B tel que (, ) = − est le deuxième sommet
du polygone régulier de côté AB.

En pratique on trace le pentagone régulier ADGJM (sens direct).

À partir du point G, on trace le triangle équilatéral GBL
(sens rétrograde).

En reportant 14 fois la longueur AB sur le cercle, on obtient
le polygone régulier ABCDEFGHIJKLMNP.

15.b. Construction avec une médiatrice

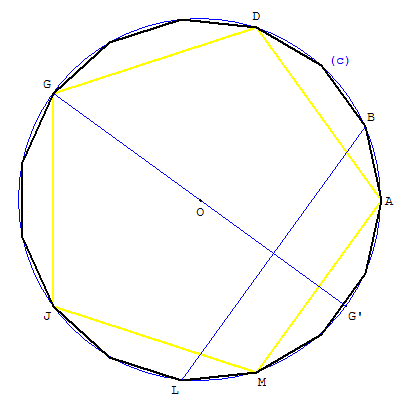
Construire le pentagone régulier ADGJM inscrit dans le cercle (c) de centre O.

Placer le point G’ symétrique de G par rapport à O.

La médiatrice de [OG’] coupe le cercle (c)
en deux points B et L, sommets du pentédécagone.

Justification

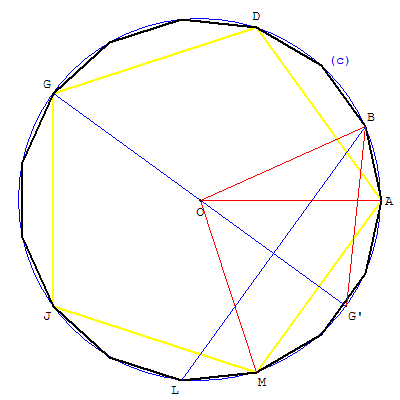
Le triangle OBG’ est équilatéral,
car OB = OG’ comme rayons et OB = G’B car B est sur la médiatrice de [OG’].

L'angle MÔA de deux rayons du pentagone est de 72°.
G’ÔA = MÔA = 36°.

AÔB = G’ÔB − G’ÔA = 60° − 36° = 24°, angle deux rayons du pentédécagone.

15.c. Construction au compas

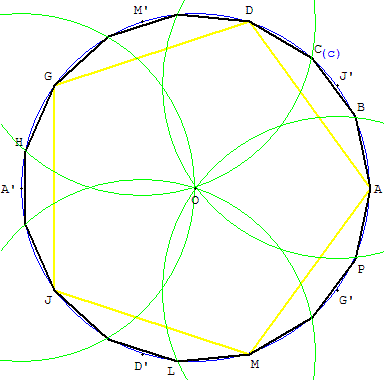
Construire le pentagone régulier ADGJM de centre O.

Placer les points A’, D’, G’, J’, M’ symétriques
de A, D, G, J, M par rapport à O.

Les points du pentédécagone sont les points d'intersection du
cercle (c) avec les cercles de centres A’, D’, G’, J’, M’
passant par le centre O.

Justification

G’OB est un triangle équilatéral de côtés égaux au rayon r
du cercle circonscrit, G’ÔB = 60°.

G’ÔA = MÔA = 36° (angle au centre du pentagone).

AÔB = G’ÔB − G’ÔA = 60° − 36° = 24° est l'angle au
centre du pentédécagone et le point B est bien un sommet.

Article exporté dans WikiPédia : Pentédécagone

Pentédécagones croisés

Le nombre de polygones réguliers croisés de n côtés est égal
au nombre de nombres premiers avec n contenus dans la
suite 2, 3…, .
Il y a trois pentédécagones croisés que l'on obtient en joignant
les sommets de deux en deux, de quatre en quatre ou de sept en sept.

17. Heptadécagone (polygone de Gauss)

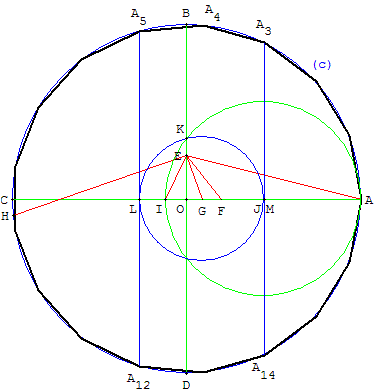
Cette méthode employée par Gauss en 1796,
montre que le polygone régulier de 17 côtés
est constructible à la règle et au compas.

Pour inscrire ce polygone dans un cercle (c), de centre O,
tracer deux diamètres [AC] et [BD] perpendiculaires

Soit E le point de [OB] tel que OE = OB,
la droite (EF) est la bissectrice de OÊA et la droite (EG)
est la bissectrice de OÊF (OÊG = OÊA).

(HE) est la perpendiculaire en E à (EG),
la droite (EI) est la bissectrice de HÊG.

Le cercle de diamètre [IA], centré en J, rencontre [OB] en K.

Le cercle de centre G, passant par K coupe [AC] en L et M
(presque confondu avec J).

Les parallèles à (BD) passant L et M coupent le cercle (c) en
A₅, A₁₂, A₃, A₁₄, points du polygone.

La médiatrice de [A₃ A₅] coupe le cercle en A₄. [A₃ A₄] et [A₄ A₅]
sont deux côtés de l'heptadécagone.

Table des matières

Dans d'autres pages du site

Triangle équilatéral

Quadrilatères

Carré

GeoGebraBook : Polygones réguliers

Les Éléments d'Euclide

Les grands problèmes de la géométrie grecque

Sur ordinateur, cette page pour grand écran

Google friendly

Copie twitter : t.co/jGgmNRoVgQ

Copyright 2006 - © Patrice Debart