Descartes et les Mathématiques
Aires du parallélogramme et du trapèze
Des images aux formules : partage de parallélogrammes, de trapèze - Figures réalisées avec GéoPlan.
Sommaire
4. Deux parallélogrammes d'aires égales
5. Partage d'un parallélogramme en deux paires de triangles de même aire
Multiplication de l'aire d'un parallélogramme
sur tablette ou smartphone, bascule automatique vers la version mobile
Dans d'autres pages du site
Démonstrations avec la méthode des aires :
théorème de Thalès
théorème de Pythagore
Aire d'un quadrilatère non convexe : prenons de la hauteur
Calcul d'aire minimum : minimum-maximum
Analyse en option 1ère L - TL
Aire d'un triangle à l'intérieur d'un parallélogramme
Carré d'aire cinq fois plus petite
Quadrilatère dans un rectangle : napperon
1.a. Aire d'un parallélogramme
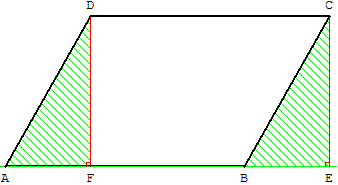
Calcul de l'aire de la surface du parallélogramme quelconque
Classe de cinquième
Transformer un parallélogramme en rectangle
Soit ABCD un parallélogramme, E et F les projections orthogonales de C et D sur (AB).
Le rectangle FECD a même aire que le parallélogramme, car les triangles rectangles ADF et BCE sont isométriques.
Formule de l'aire du parallélogramme
Aire(ABCD) = AB × DF = a × h = base × hauteur
où a = AB = CD et h = DF = CE.
L'aire d'un parallélogramme a pour mesure le produit de sa base par sa hauteur.
Dans la recherche d'images « aire parallélogramme », Google préfère la mauvaise copie d'HauEtFort, à cette figure originale !
1.b. Aire d'un parallélogramme, sans la hauteur
Chaque diagonale partage le parallélogramme en deux triangles de même aire.
En effet, les deux triangles sont symétriques par rapport au milieu de la diagonale.
Aire(ABCD) = 2 Aire(ABD) = 2 Aire(BCD).
Technique GéoPlan : cette propriété est utilisée pour calculer l'aire d'un parallélogramme, sans la hauteur, en doublant l'aire d'un des triangles formés par une diagonale et les deux côtés consécutifs correspondants.
Calculer s1 avec le menu :« Créer>Numérique>Calcul géométrique>Aire d'un triangle »
s1 aire du triangle ABC (unité de longueur Uoxy) s = 2s1
Calcul traditionnel, avec la hauteur, de la surface du parallélogramme avec GéoPlan
Il est aussi possible de faire faire le calcul en nommant la base b et h la hauteur dans le menu :
« Créer>Numérique>Calcul géométrique>Longueur d'un segment »
b = AB (unité de longueur Uoxy) h = DF (unité de longueur Uoxy)
Puis faire le calcul avec l'option « Créer>Numérique>Calcul algébrique » avec l'expression du calcul : bh ; ayant pour nom du calcul : s
s = bh
Télécharger la figure GéoPlan air_para.g2w
1.c. Théorème de la tringle (à rideaux)
Les Éléments d'Euclide - Lèvre I - Proposition 35
Méthode du cisaillement
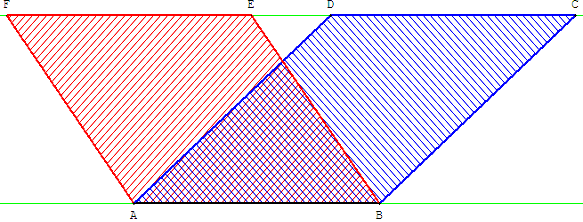
Deux parallélogrammes, de même base, entre deux mêmes parallèles, sont d'aires égales :
Si ABCD et ABEF sont deux parallélogrammes tels que E (et F) sont des points de la droite (CD), alors ils ont même aire.
En effet ils ont même base et même hauteur.
Télécharger la figure GéoPlan thm_tringle.g2w
1.d. Parallélogramme et triangle de même base
Les Éléments d'Euclide - Livre I - Proposition 41
Si un parallélogramme et un triangle ont une même base, et sont entre mêmes parallèles ; le parallélogramme sera [d'aire] double du triangle.
Méthode des aires : démonstration utilisant les propriétés d'Euclide : « les triangles ou les parallélogrammes qui ont la même hauteur sont l'un relativement à l'autre comme leurs bases ».
2. Aire du losange
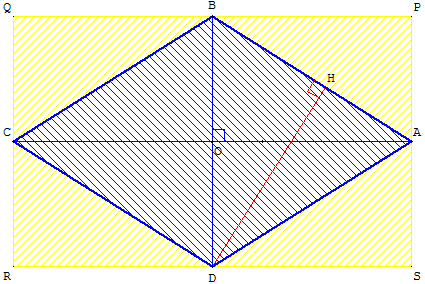
Deux méthodes de calcul de la surface du losange selon qu'on le considère comme un parallélogramme ou comme un quadrilatère orthodiagonal.
Un losange est un parallélogramme.
Son aire a pour mesure le produit de sa base par sa hauteur.
A(ABCD) = AB × DH.
Un losange est un quadrilatère orthodiagonal
Le losange ABCD est inscrit dans le rectangle PQRS.
L'aire du rectangle est égale au produit des longueurs des diagonales AC × BD.
L'aire du losange est alors 
AC × BD.
L'aire d'un losange est égale à la moitié du produit des longueurs des diagonales.
Télécharger la figure losange.g2w
3. Aire du trapèze
De l'objet réel à sa modélisation
Classe de 5e
Géométriser un problème, c'est transposer le problème, qui peut être concret ou non, le plus souvent spatial au niveau du collège, dans le cadre de la géométrie afin de le simplifier et de le résoudre. C'est le cas, par exemple, lors du calcul de l'aire d'un champ.
Le champ réel a une certaine forme. Le processus de modélisation géométrique comporte deux étapes :
– assimilation du champ à une surface plane limitée par des portions de lignes droites ;
– assimilation de cette surface à un polygone élémentaire (trapèze dans l'exemple qui suit) ou un agencement de plusieurs polygones simples.
Le recours à un schéma pour « simplifier » et s'approprier la situation étudiée illustre ce passage de la réalité au domaine de la géométrie. La figure géométrique intervient ainsi comme une
maquette de la réalité. Ces transferts sont déjà travaillés à l'école primaire.
Cette habitude du recours à une visualisation simplificatrice peut paraître naturelle à certains élèves à l'entrée au collège, mais reste à construire pour beaucoup d'autres.
Il est donc indispensable de travailler cette compétence.
Une fois le transfert effectué dans le cadre géométrique, la résolution du problème repose sur des propriétés attachées aux objets, qui sont utilisées alors comme des modèles.
Le modèle référant possède un statut mathématique organisé en propriétés.
Le schéma « simplifie » donc, mais ajoute aussi des éléments de connaissance.
Ainsi, dans l'exemple du champ trapézoïdal, on passe du champ à un trapèze, puis, enfin au « Trapèze » dont on peut calculer l'aire, par décomposition en triangles et rectangle, à l'aide de hauteurs issues de deux sommets qui ne correspondent à rien dans la réalité.
Ressources pour les classes de 6e, 5e, 4e, et 3e - Géométrie au collège
Projet de document d'accompagnement mathématique - Juillet 2007
Définition
Trapèze : quadrilatère convexe ayant deux côtés opposés parallèles ; les deux côtés parallèles sont les bases : la grande base et la petite base.
Voir : quadrilatères
Trapèzes dans la planche à clous
Calculer l'aire d'un trapèze :
Dans les paragraphes suivants, ABCD désigne un trapèze de grande base [AB] et de petite base [CD] parallèle à (AB).
3.a. Décomposition du trapèze en triangles et rectangle
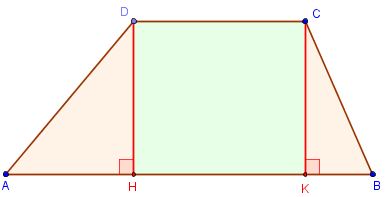
Cas où [HK], projection de la petite base [DC], est inclus dans [AB].
On peut calculer l'aire, par décomposition en un rectangle et deux triangles rectangles, à l'aide des hauteurs issues des deux sommets de la petite base.²
Figure interactive dans GeoGebraTube :
Trapèze - Aire par découpage
Calcul de l'aire d'un trapèze
Dans ce cas de figure, avec b = AB, b’ = CD, h = DH, le trapèze est un rectangle HDCK (d'aire b’h) auquel on accole deux triangles rectangles ADH et KBC (dont la somme des aires est (AH + BK)h/2 = (b –b’)h/2).
Aire(ABCD) = b’h + (b – b’)h/2 = 
× h.
Formule de l'aire du trapèze
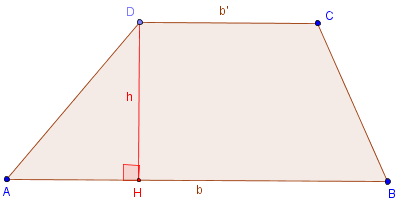
La surface d'un trapèze a pour mesure le produit de la moyenne des bases par sa hauteur :
b = AB, b’ = CD, h = DH : Aire(ABCD) = × h.
Figure interactive dans GeoGebraTube : Trapèze - Formule de l'aire
WikiPédia : Trapèze
Wikiversité : Mesure en géométrie : Aire
3.b. Découpage du trapèze-en deux triangles
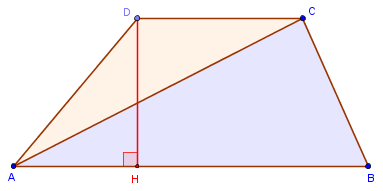
Calculer l'aire en découpant le trapèze en deux triangles de même hauteur.
Soit h = DH la hauteur, b = AB la première base, et b' = CD la deuxième.
On peut considérer les triangles ACB et ADC, respectivement de bases b et b', et de hauteur commune h.
S = hb /2 + hb' /2 = h (b + b')/2.
Figure interactive dans GeoGebraTube : Trapèze - Découpage en 2 triangles
3.c. Transformer le trapèze en rectangle
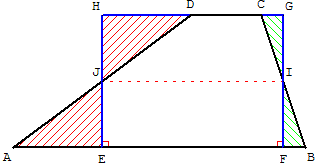
Soit I et J les milieux des côtés [BC] et [AD]. D'après la propriété de Thalès,
IJ est égal à la moyenne des bases.
On a m = IJ = .
E et F les projections orthogonales de J et I sur (AB) ainsi que G et H les projections orthogonales de I et J sur (CD).
Le rectangle EFGH a même aire que le trapèze ABCD, car les triangles rectangles
IGC et IFB sont isométriques, de même que les triangles JHD et JEA.
On retrouve Aire(ABCD) = Aire(EFGH) = EF × EH = m h = × h.
Télécharger la figure GéoPlan aire_trapeze.g2w
3.d. Doubler un trapèze pour obtenir un parallélogramme
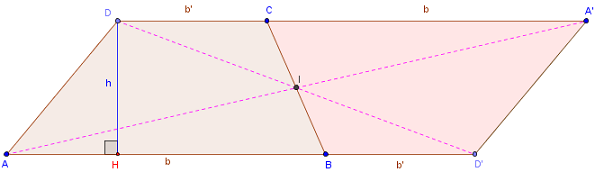
ABCD est un trapèze de grande base [AB], et de petite base [CD] parallèle à (AB).
I le milieu du côté [BC].
La symétrie de centre I transforme A en A’ et D en D’.
Les points A, B et C’ sont alignés comme les points D, C et A’.
(BD’) est parallèle à (A’C). BD’A’C est un trapèze de même aire que ABCD et on a :
b = AB = A’C, b’ = CD = A’C, h = CH.
(AD) est parallèle à (A’D’). AD’A’D est un parallélogramme de base AD’ = b + b’.
Aire(AD’A’D) = AD’ × CH = (b + b’) × h.
Or Aire(AD’A’D) = Aire(ABCD) + Aire(BD’A’C) = 2 Aire(ABCD), soit 2 Aire(ABCD) = (b + b’) × h.
On retrouve Aire(ABCD) = × h.
Figure interactive dans GeoGebraTube : Doubler un trapèze pour obtenir un parallélogramme
3.e. Transformer un trapèze en parallélogramme
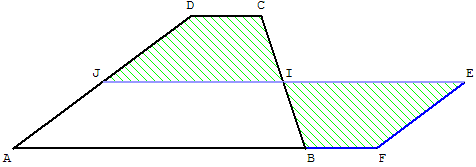
Le trapèze a même aire que celle du parallélogramme AFEJ.
Aire(ABCD) = Aire(AFEG) = AF × h = (b + b’) × h.
Télécharger la figure GéoPlan aire_trapeze_4.g2w
3.f. Transformer un trapèze en rectangle
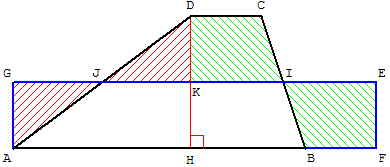
Le trapèze a même aire que celle du rectangle AFEG.
Aire(ABCD) = Aire(AFEG) = AF × KF = (b + b’) × h.
Télécharger la figure GéoPlan aire_trapeze_3.g2w
3.g. Transformer un trapèze en triangle
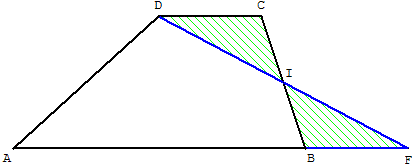
Le trapèze a même aire que celle du triangle ADF.
Aire(ABCD) = Aire(ADF) = AF × h = (b + b’) × h.
Télécharger la figure GéoPlan aire_trapeze_5.g2w
Voir : trapèze complet et théorème du trapèze (classe de première)
3.h. Deux triangles dans un trapèze
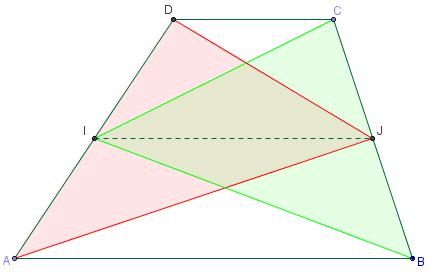
ABCD est un trapèze tel que (AB) est parallèle à (CD).
I et J sont les milieux des côtés [AD] et [BC].
Les triangles ADJ et BCI sont-ils de même aire ?
Indications
Tracer la droite (IJ) et montrer, par la propriété de Thalès, qu'elle est parallèle à (AB) et (CD).
Les triangles IJA et IJB ont même aire d'après la propriété du trapèze.
De même, les triangles IJD et IJC ont même aire.
Les triangles ADJ et BCI ont même aire comme réunion disjointe de triangles deux à deux de même aire.
Figure interactive dans GeoGebraTube : deux triangles dans un trapèze
4. Deux parallélogrammes d'aires égales
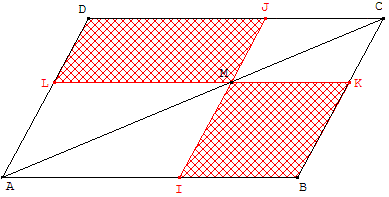
M est un point variable sur la diagonale [AC] d'un parallélogramme ABCD.
Par M, on trace deux parallèles aux côtés du grand parallélogramme.
Démontrer que les aires des deux parallélogrammes hachurés sont égales.
Vérification assez facile avec GéoPlan : le logiciel ne sait pas calculer l'aire d'un parallélogramme, mais il sait trouver la moitié de cette aire :
l'aire d'un triangle formé par deux côtés et une diagonale.
Éléments d'Euclide : livre I, Proposition 43
Les éléments d'Euclide - Livre I - Proposition 43
Classe de cinquième
Montrer qu'une diagonale d'un parallélogramme le partage en deux triangles d'aires égales.
Démontrer que les aires hachurées sont égales en utilisant cette propriété dans les parallélogrammes ABCD, AIML et MKCJ.
Partage d'un parallélogramme en quatre - hauteur
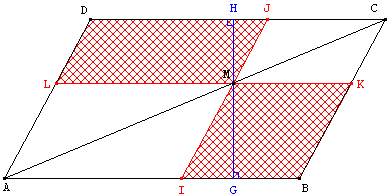
Classe de troisième - assez difficile
Indication : (AB) étant parallèle à (CD), la propriété de Thalès dans les triangles rectangles AMG et CMH permet d'écrire : 
= 
.
(AD) étant parallèle à (BC), avec la propriété de Thalès dans les triangles ALM et CKM on a :
= 
.
Par transitivité = .
Le produit des « extrêmes » est égal au produit des « moyens » :
KM × MG = LM × MH.
Aire(IBKM) = Aire(LMJD).
Télécharger la figure GéoPlan hom_par3.g2w
Cas particulier de rectangles en classe de quatrième, voir : les Éléments d'Euclide
Deux triangles d'aires égales dans un parallélogramme
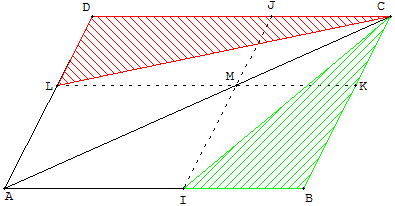
M est un point variable sur la diagonale [AC] du parallélogramme ABCD.
Par M, on trace deux parallèles aux côtés du grand parallélogramme.
Les aires des deux triangles hachurés sont égales.
Télécharger la figure GéoPlan hom_par6.g2w
5. Partage d'un parallélogramme en deux paires de triangles
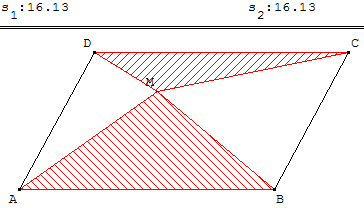
Partage en triangles d'aires égales
Classe de cinquième
Un fermier possède un très grand champ en forme de parallélogramme ABCD à l'intérieur duquel se trouve un puits en un certain point M.
Se sentant mourir, il donne à son fils Pierre les deux champs triangulaires MAB et MCD et tout le reste à son autre fils Jean.
Un des frères est-il défavorisé ?
Il est possible de simplifier cet exercice en considérant un champ rectangulaire.
Formulation plus classique :
M est un point à l'intérieur d'un parallélogramme ABCD.
Démontrer que la somme des aires des deux triangles hachurés est égale à celle des deux triangles non hachurés.
Partage d'un parallélogramme en deux - hauteur
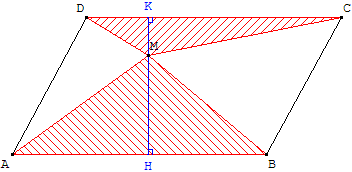
Indication : tracer les points H et K projections orthogonales de M sur (AB) et (CD). (HK) est perpendiculaire à (AB) et à (CD).
(HM) est une hauteur de ABM et Aire(ABM) = AB × HM.
(MK) est une hauteur de CDM et Aire(CDM) = CD × MK.
Dans le parallélogramme ABCD, les côtés [AB] et [CD] sont de même longueur.
D'où Aire(ABM) + Aire(CDM) = AB × HM + AB × MK
= AB × (HM + MK).
Aire(ABM) + Aire(CDM) = AB × HK = Aire(ABCD).
La somme des aires des deux triangles hachurés est égale à la moitié de l'aire du parallélogramme. Celle des deux triangles non hachurés est égale à l'autre moitié. Le partage est équitable.
Télécharger la figure GéoPlan para_aire.g2w
6. Théorème du papillon dans un trapèze
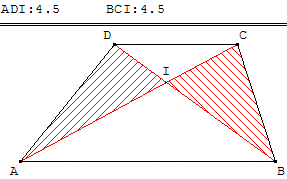
Dans le cas particulier où AB = DC, cette figure permet également d'étudier deux triangles de même aire dans un parallélogramme.
ABCD est un trapèze. Les diagonales se coupent en I.
Classe de 5e
6.a. Les aires des deux triangles hachurés ADI et BCI sont égales.
Théorème du papillon : si la droite (AB) est parallèle à la droite (DC) alors Aire(ADI) = Aire(BCI).
Indication : tracer les points H et K projections orthogonales de I sur (AB) et (CD). (HK) est perpendiculaire à (AB) et à (CD).
Les triangles ABC et ABD ont même aire, égale à la moitié de la base AB, multipliée par la hauteur de longueur HK.
En enlevant à ces deux triangles la surface du triangle CDI, on a bien Aire(ADI) = Aire(BCI).
Théorème du papillon et hauteur
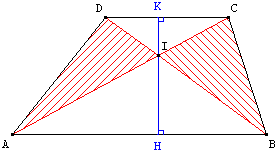
Classe de 3e
6.b. Montrer que le rapport 
est égal au carré du rapport 
(Thalès…).
Indication : (AB) étant parallèle à (CD), la propriété de Thalès dans les triangles ABI et CDI permet d'écrire :
= 
= k.
De même, la propriété de Thalès dans les triangles rectangles AHI et CKI permet d'écrire :
= = k.
Aire(ABI) = AB × HI et Aire(CDI) = CD × KI d'où :
= × = 
= k2 car = = k.
En classe de seconde, on dira que les triangles ABI et CDI, ayant leurs trois angles respectivement égaux, sont semblables avec un coefficient d'agrandissement k. Cette démonstration montre que le rapport de leurs aires est k2.
Télécharger la figure GéoPlan trap_aire.g2w
Table des matières
Dans d'autres pages du site
Aires et triangles ; chevron et parallélogramme
Multiplication de l'aire d'un parallélogramme
Expressions clés : calculer laire du parallélogramme, aire parallélogramme sans hauteur, aire parallélogramme rectangle, aire parallélogramme diagonales, formule aire trapèze, calculer l'aire du trapèze
Page no 131, réalisée le 3/12/2008
modifiée le 17/4/2013