Descartes et les Mathématiques

Empilements dans le plan

Ranger des disques ou des carrés dans un cercle, dans un triangle ou dans un polygone.

Sommaire

1. Inscrire des disques dans un cercle, un triangle, un carré ou dans un polygone régulier

2. Inscrire des carrés dans un cercle

Placer des cercles dans des polygones ou dans un cercle.

1. Inscrire des disques, de même rayon, dans une figure

Je « thème » les mathématiques

Construction sous contrainte : reproduire une figure pour créer un Sangaku.

Remplir un disque ou un polygone régulier avec des cercles, de même rayon, tangents deux à deux.
Inscrire n cercles, de rayon r maximal, dans :

• un polygone régulier de m côtés,
• un rectangle (problème d'optimisation du rangement de boites de conserve dans un carton),
• un cercle :
  une solution est de construire un polygone régulier de n côtés, circonscrit à ce cercle, et d'y inscrire n cercles :
    – tracer les n triangles isocèles identiques qui ont pour côtés deux rayons du cercle et pour base un côté du polygone.
    – construire le cercle inscrit dans chaque triangle. 
  On obtient ainsi n cercles tangents deux à deux entre eux et tangents au grand cercle. C'est optimal de n = 3 à n = 5.
  Mais pour n = 7, il suffit de tracer un hexagone circonscrit…

Deux cercles dans un carré

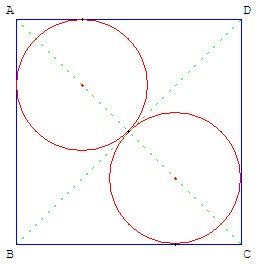
Le centre du cercle inscrit dans le triangle ABD est l'intersection de la diagonale [AC] avec la bissectrice de l'angle ABD.

Télécharger la figure GéoPlan deux_cercle_ds_carre.g2w

Cercles de rayons différents, voir aussi :
  • deux cercles tangents, tangents à un carré,

  • résoudre avec l'algèbre des problèmes de géométrie.

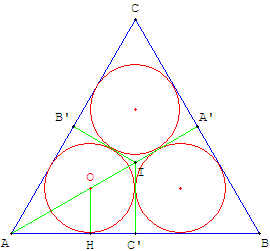
Trois cercles dans un triangle équilatéral

Les trois cercles sont inscrits dans les cerfs-volants formés par les côtés et les médiatrices du triangle.
Les centres des cercles sont à l'intersection des bissectrices des cerfs-volants.

Cette figure est aussi optimale pour deux cercles inscrits dans le triangle ;
comment le prouver ?

Calculs

Soit r le rayon des cercles et a le côté du triangle équilatéral.

Dans le triangle AIC’, rectangle en C’, d'angle IAC’ = 30°,
on a  AC’ = ; OH = HC’ = r ;
et dans le triangle rectangle AHO, d'angle HOA = 60°,
on trouve AH = OH tan(60°) = r .

AC’ = = AH + HC’ = r ( + 1).

D'où r = a/( + 1) = a ( - 1)/4 ≈ 0,183 a.

Télécharger la figure GéoPlan trois_cercle_ds_tri.g2w

Trois cercles dans un cercle

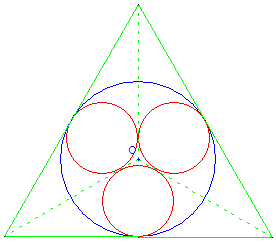
Construire un triangle équilatéral circonscrit au cercle et inscrire trois cercles dans les triangles isocèles qui ont pour côtés deux rayons du cercle et pour base un côté du triangle équilatéral.

On a r = R/ (1+2/) ≈0,464 R (R rayon du grand cercle, r rayon des petits cercles inscrirs)

Télécharger la figure GéoPlan trois_cercle_ds_cercle.g2w

Six cercles dans un triangle équilatéral

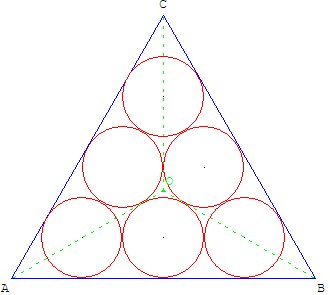
Dans un triangle équilatéral ABC de centre O, il est possible de compléter les trois cercles inscrits dans les triangles OAB, OBC, OAC pour obtenir six cercles, de même rayon, inscrits dans le triangle.

Télécharger la figure GéoPlan six_cercle_ds_tri.g2w

Quatre cercles dans un cercle

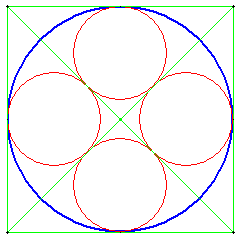
Construire un carré circonscrit à ce cercle et inscrire quatre cercles dans les triangles isocèles qui ont pour côtés deux rayons du cercle et pour base un côté du carré.

On a r = R/(1 + ) = R/( - 1) ≈ 0,414 R (R rayon du grand cercle, r rayon des petits cercles)

Télécharger la figure GéoPlan quatre_cercle_ds_cercle.g2w

Trois cercles dans un carré

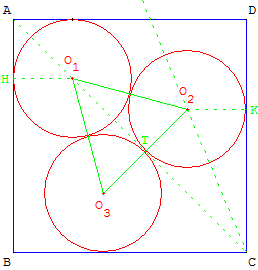
Le côté [O₁O₂] du triangle équilatéral O₁O₂O₃, d'axe [AC], fait un angle de avec (AD).
La projection de la ligne brisée HO₁O₂K sur (AD) mesure
2r(1 + cos ). D'où le calcul de r = 0,2543 AD.

Télécharger la figure GéoPlan trois_cercle_ds_carre.g2w

Cinq cercles dans un carré

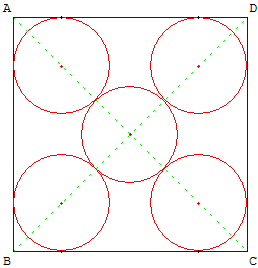
Les cercles sont centrés sur les diagonales.

Pas de construction géométrique trouvée. Il faut résoudre ce problème avec l'algèbre :
Si a est la longueur du côté du carré, calculer le rayon r des cercles avec la relation a = (2+2)r.

Télécharger la figure GéoPlan cinq_cercle_ds_carre.g2w

Cinq cercles dans un pentagone

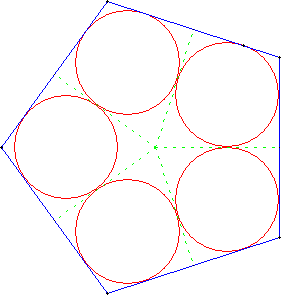
Les cercles sont inscrits dans les cerfs-volants formés par les côtés et les médiatrices du pentagone régulier.

Télécharger la figure GéoPlan cinq_cercle_ds_penta.g2w

Cinq cercles dans un cercle

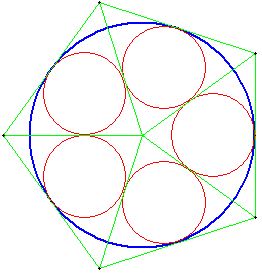
Construire un pentagone régulier circonscrit à ce cercle et inscrire cinq cercles dans les triangles isocèles qui ont pour côtés deux rayons du cercle et pour base un côté du pentagone.

On a r ≈ 0,37 R (R rayon du grand cercle, r rayon des petits cercles)

Télécharger la figure GéoPlan cinq_cercle_ds_cercle.g2w

Sept cercles dans un hexagone

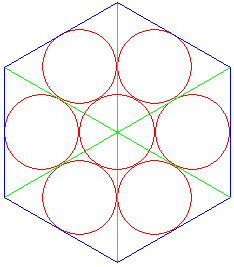
Avec des cercles inscrits dans un triangle équilatéral, il est possible d'inscrire six cercles dans un hexagone régulier et on peut rajouter un septième cercle de même rayon au centre de l'hexagone.

Télécharger la figure GéoPlan sept_cercle_ds_hexa.g2w

Sept cercles dans un cercle

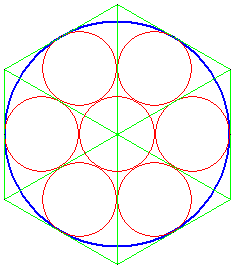
Remplir un cercle avec 6 disques

Construire un hexagone régulier circonscrit au cercle et inscrire six cercles dans les triangles équilatéraux.
On peut rajouter un même septième cercle au centre du grand cercle.

Le rayon des petits cercles est égal au tiers du rayon du grand cercle.

Cercles inscrit dans un cercle

2. Inscrire des carrés, de mêmes côtés, dans un disque

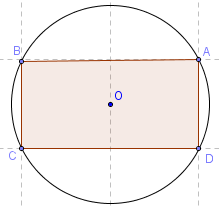
Ces inscriptions de carrés dans un disque sont-elles optimales ? Qui dit mieux ?

Deux carrés dans un cercle

Deux carrés, de côté 1, dans un disque de rayon r = 1,12.

Figure interactive dans GeoGebraTube : deux carrés dans un cercle

Trois carrés dans un cercle

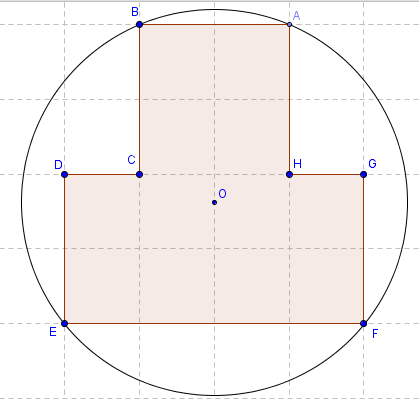
Trois carrés, de côté 2, dans un disque de rayon r = 2,6.

Figure interactive dans GeoGebraTube : trois carrés dans un cercle

Autre configuration non optimale : trois carrés, de côté 1, autour d'un triangle équilatéral de côté 1, dans un disque de rayon r =1,38 ;
voir la figure interactive dans GeoGebraTube : trois carrés autour d'un triangle équilatéral

Cinq carrés dans un cercle

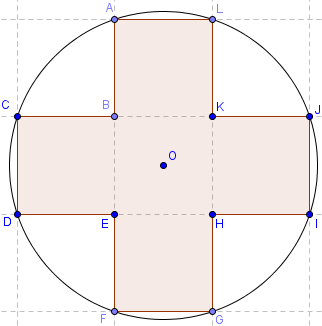
Cinq carrés, de côté 1, dans un disque de rayon r = 1,58.

Figure interactive dans GeoGebraTube : cinq carrés dans un cercle

Huit carrés dans un cercle

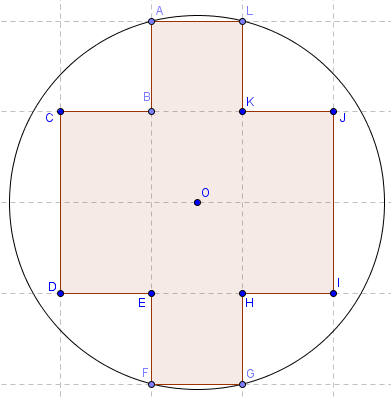
Huit carrés, de côté 1, dans un disque de rayon r = 2,06.

Figure interactive dans GeoGebraTube : huit carrés dans un cercle

Table des matières

Mobile friendly

Copie twitter : t.co/Hzt1pG6hKk

Dans d'autres pages du site

Partager un triangle en triangles d'aires égales

Le cercle au lycée

Trois cercles égaux à l'intérieur d'un triangle

Seconde : Problèmes d'optimisation

Théorème de Descartes