Descartes et les Mathématiques
Rectangle inscrit dans un rectangle
Inscrire un petit rectangle dans un grand. Cinq variantes d'un problème non résoluble à la « règle et au compas ».
Sommaire
1. Question sur le forum cadxp
2. La boite à lettres
Variante proposée aux olympiades académiques de 2004 : mise en boite
1. Question sur le forum cadxp
Posté par Patrick le 27/7/2004 à 23:22
Un problème de géométrie intéressant soulevé par un utilisateur CAO (Tom), sur le forum Planetar :
1\ la largeur du petit rectangle, par exemple 10 unités.
2\ je veux que chaque sommet du petit rectangle soit situé sur un côté différent du grand rectangle, et ce quel que soit le grand rectangle initial.
La solution peut être manuelle, mathématique ou algorithmique de façon à être implémentée en Lisp ou VBA par exemple.
Aucune solution n'a été trouvée pour l'instant…
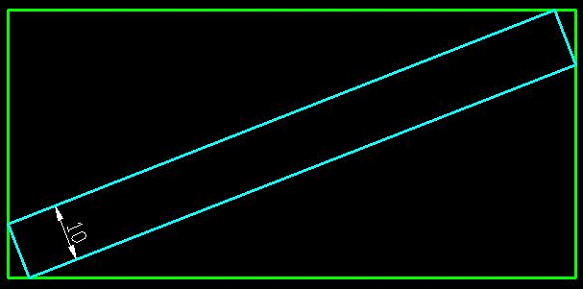
Rectangle inscrit dans un rectangle : une solution
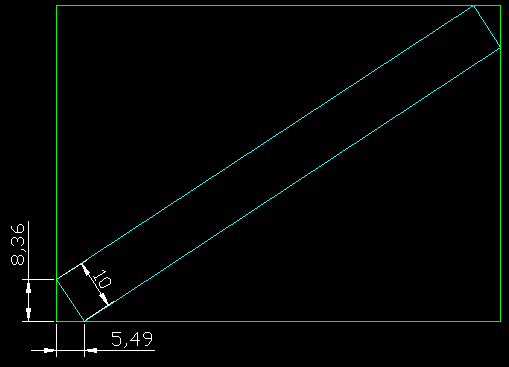
L = 75 longueur du grand rectangle vert et H = 54 largeur ; l = 83.14 longueur du petit rectangle bleu.
Un peu de maths…
Variables :
L = AB, longueur du grand rectangle ABCD vert,
H = AD, hauteur (largeur) de ce même rectangle,
l = NP, longueur du petit rectangle MNPQ bleu,
h = MN =10, hauteur de ce même rectangle.
x = AN, petit côté du petit triangle rectangle AMN du coin,
y = AM, grand côté de ce triangle ;
x’ = NB, grand côté du grand triangle BNP,
y’ = BP, petit côté de ce triangle.
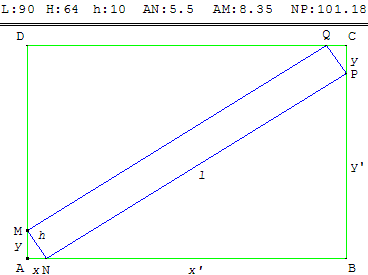
Un exemple de solution avec GéoPlan
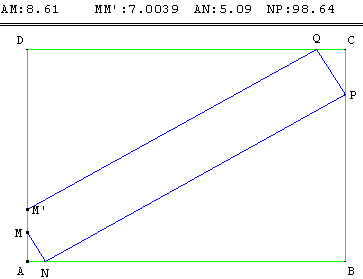
Ligne brisée permettant la recherche
Télécharger les figures GéoPlan cadxp.g2w et cadxp_2.g2w
Mise en équation
x + x’ = L
y + y’ = H
x2 + y2 = h2 d'après le théorème de Pythagore, dans le triangle AMN.
x / y’ = y / x’ (= h / l) est égal au rapport de similitude des triangles rectangles AMN et BNP.
Pour résoudre ce système de quatre équations à quatre inconnues, substituer les deux premières équations à la dernière :
x (L - x) = y (H - y) d'où Lx - x2 = Hy - y2 et Lx - x2 - Hy + y2 = 0.
La relation de Pythagore permet de calculer y2 = h2 - x2 donc -2 x2 + Lx + h2 = H y.
Il suffit d'élever au carré et de substituer à nouveau y2 : (-2 x2 + Lx + h2)2 = H2(h2 - x2).
On obtient une équation du quatrième degré qui a deux solutions réelles de signes contraires, seule la solution positive convient.
Il n'est pas possible d'obtenir une solution exacte, mais une calculatrice comme la TI-92 ou le logiciel Derive permettent de trouver une solution approchée.
Par exemple, pour L = 75 et H = 54 la TI-92 trouve en quelques minutes la solution du premier exemple x = 5,49.
Géométrie dynamique
Créer, à partir d'un point M de [AD], une ligne brisée MNPM’ telle que MN = h et continuer à angles droits. En général, M et M’ sont distincts.
Déplacer le point M pour le faire coïncider avec le point M’ pour fermer le rectangle et trouver manuellement une solution approchée.
2. Variante : paquet dans une boite à lettres
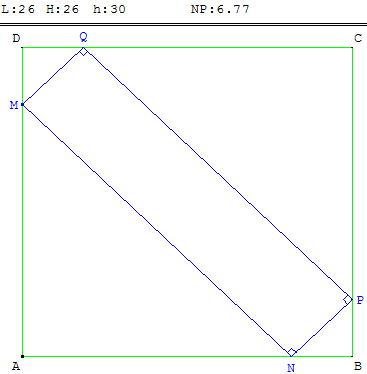
Une boite à lettres normalisée doit, suivant les spécifications de la poste française, respecter les dimensions :
H = 26 cm × L = 26 cm × P = 34 cm.
Déterminer la largeur d'un paquet dont la face rectangulaire de longueur 30 cm a été insérée suivant la figure ci-contre.
Indication
Avec GéoPlan on trouve l = NP = 6,7 cm.
Table des matières
Dans d'autres pages du site
Quadrilatère dans un rectangle : napperon
Mobile friendly
Copyright 1986 - © Patrice Debart
|
Page no 82, créée le 6/9/2004 |