Descartes et les Mathématiques
La géométrie des Olympiades 2002 à 2005
Choix de sujets de géométrie des annales académiques et indications de solutions avec GéoPlan-GéoSpace
Sommaire
2005
1. Un ennéagone
Carrés inscrits dans un triangle
2004
3; Pliage du coin d'une feuille
Carré d'aire 5 fois plus petite
2002
Sujets traités dans d'autres pages du site
2002
Deux cercles tangents, tangents à un carré
2004
Dans d'autres pages du site
Sujet national
Transformer un quadrilatère en triangle
Amiens
Partage de l'angle d'un triangle en 4 : construction de-ci, de-là
Existe-t-il un triangle ABC tel que la hauteur issue de A, la bissectrice de l'angle BÂC et la médiane relative au côté [BC] partagent l'angle BÂC en quatre angles de même mesure ?
Olympiades 2004 - Dijon
Réciproque : prouver qu'un triangle ayant angle partagé en 4 angles de même mesure par la hauteur, la bissectrice et la médiane issues du sommet de cet angle, dans cet ordre, est obligatoirement rectangle.
Montpellier
Construction d'une parabole, à la manière des compagnons bâtisseurs du Moyen-Âge.
Toulouse
2005
1. Un ennéagone
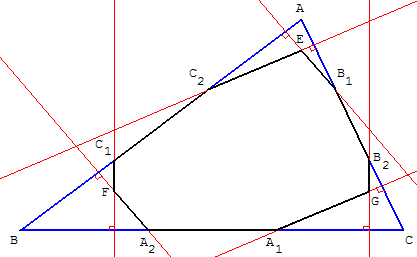
Aix-Marseille
Un ennéagone est un polygone à neuf côtés.
On considère la figure suivante dans laquelle AB1 = B1B2 = B2C ; BC1 = C1C2 = C2A et BA2= A2A1 = A1C.
1. Démontrer que la droite (AE) est perpendiculaire à la droite (BC).
De même, la droite (BF) est perpendiculaire à la droite (AC) et la droite (CG) est perpendiculaire à la droite (AB) (on ne demande pas de le démontrer).
On note H le point d'intersection des droites (AE), (BF) et (CG).
2. Quel est le rapport de l'aire de l'ennéagone (A1A2F C1C2E B1B2G) sur celle du triangle (ABC) ?
1.b. Solution
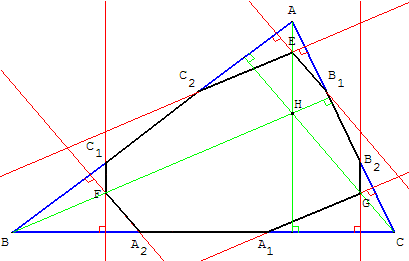
1. • Les points A, C2 et B sont alignés dans cet ordre.
Les points A, B1 et C sont alignés dans cet ordre.
= 
= 
D'après la réciproque du théorème de Thalès, les droites (B1C2) et (BC) sont parallèles.
• E est l'orthocentre du triangle (AB1C2) car les droites (B1E) et (C2E) sont, par construction, deux hauteurs de ce triangle.
(AE) est la troisième hauteur de ce triangle, donc (AE) est perpendiculaire à (B1C2).
• (B1C2) et (BC) et (AE) est perpendiculaire à (B1C2) : on en déduit que (AE) est perpendiculaire à (BC).
2. • Les points A, C2 et B sont alignés.
Les points A, E et H sont alignés.
(BH) // (C2E) car elles sont toutes deux perpendiculaires à (AC).
D'après le théorème de Thalès 
= 
=
• Le quadrilatère (AC2EB1) est donc une réduction de rapport du quadrilatère (ABHC).
Donc : Aire(AC2EB1) = 
Aire(ABHC) = [Aire(ABC) - Aire(BHC)].
Par un raisonnement analogue, on montre que :
Aire(BA2FC1) = Aire(BCHA) = [Aire(ABC) - Aire(AHC)],
Aire(CB2GA1) = Aire(CAHB) = [Aire(ABC) - Aire(AHB)].
• Par addition, il vient : Aire(AC2EB1) + Aire(BA2FC1) + Aire(CB2GA1)
= [3 × Aire(ABC) - Aire(BHC) - Aire(AHC) - Aire(AHB)]
= [3 × Aire(ABC) - Aire(ABC)] = 
Aire(ABC).
L'aire de l'ennéagone (A1A2F C1C2E B1B2G) est complémentaire de l'aire précédente, dans le triangle (ABC).
On en déduit : Aire(A1A2F C1C2E B1B2G) = 
Aire(ABC).
2. Ombre d'une fenêtre
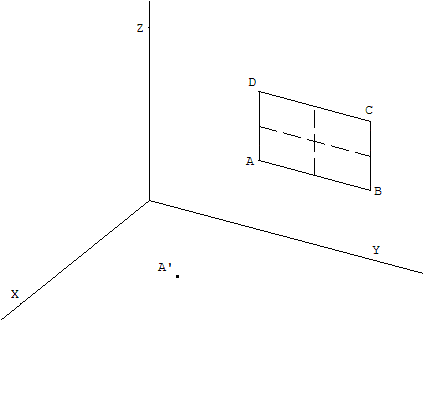
Amiens
Figure 1
La figure 1 représente une fenêtre éclairée par le soleil.
A’ est l'ombre du point A.
Tracer son ombre sur le plancher (l'ombre du coin inférieur gauche est donnée).
Figure 2
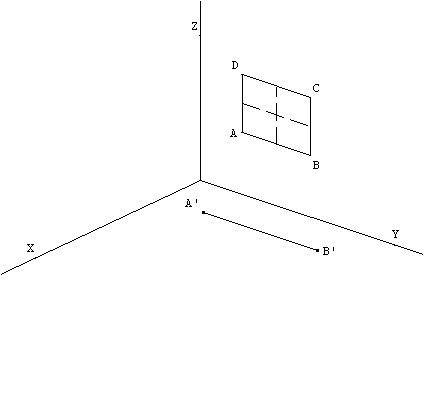
La figure 2 représente la même fenêtre éclairée cette fois par un lampadaire. Tracer son ombre sur le plancher (l'ombre du bord inférieur est donnée).
A’ est l'ombre du point A. B’ est l'ombre du point B
On réalisera les constructions, qui resteront apparentes, sur la feuille jointe qui sera rendue avec la copie.
2.b. Solutions
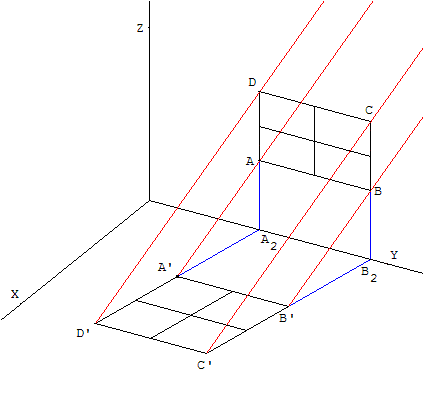
Figure 1 : fenêtre éclairée par le soleil.
On construit tout d'abord la droite (AA’).
En considérant que le soleil se trouve à l'infini, on admet que l'angle d'incidence du soleil est identique pour les quatre coins de la fenêtre.
On trace donc les parallèles à (AA’) passant par B, C et D.
On construit ensuite les points A2 et B2, pieds des deux côtés de la fenêtre.
Les points A2, A et D sont alignés, donc leurs projetés le sont aussi (idem pour B2, B et C). Or A2 et B2 sont leurs propres projetés.
On peut donc construire le point D’, point d'intersection de la parallèle à (AA’) passant par D et de la droite (A2A’).
On trace ensuite la parallèle à (A2A’) passant par B2, et les points B’ et C’ sont les points d'intersection de cette droite avec les parallèles à (AA’) passant par B et C.
Le reste de la construction se fait alors sans peine.
Figure 2 : fenêtre éclairée par le lampadaire
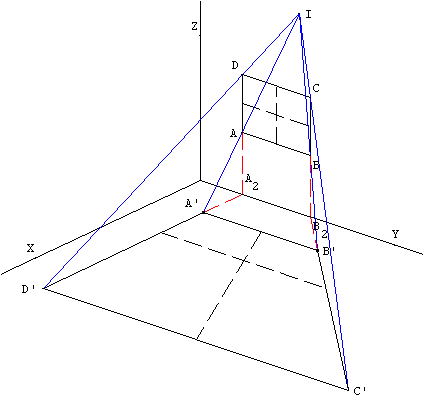
On construit tout d'abord le point d'intersection des droites (AA’) et (BB’), nommé I.
On construit ensuite les points A2 et B2, pieds des deux côtés de la fenêtre.
Les points A2, A et D sont alignés, donc leurs projetés le sont aussi (idem pour B2, B et C). Or A2 et B2 sont leurs propres projetés.
On peut donc construire le point C’, point d'intersection des droites (IC) et (B2B’), et le point D’, point d'intersection de (ID) et (A2A’).
Le reste de la construction se fait alors sans peine.
Carrés inscrits dans un triangle
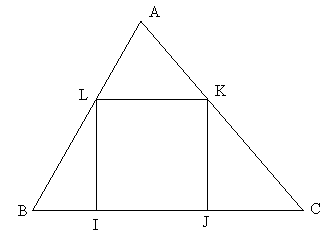
On considère un triangle ABC dont les trois angles sont aigus.
On pose BC = a, CA = b et AB = c.
On appelle h la hauteur relative à [BC] et S l'aire du triangle ABC.
On inscrit dans ce triangle le carré IJKL tel que I et J soient sur [BC], K sur [AC] et L sur [AB] comme indiqué sur la figure ci-dessous.
On dit que le carré IJKL est « posé » sur [BC]. On appelle C1 ce carré.
On peut construire, de même, deux autres carrés C2 et C3 inscrits dans le triangle ABC, l'un «posé» sur [CA], l'autre « posé » sur [AB].
1 : Exprimer le côté du carré IJKL en fonction de a et h.
2 : On suppose que a ≤ b ≤ c. Classer les trois carrés C1, C2 et C3 par ordre de grandeur.
3 : Déterminer les triangles ABC d'aire S donnée, tels que l'aire du carré IJKL soit maximale.
4 : Existe-t-il des triangles ABC d'aire S donnée, tels que les trois carrés soient d'aires maximales ?
Voir aussi : construction avec une homothétie
Cas particulier : carré inscrit dans un triangle rectangle
2004
3. Pliage du coin d'une feuille
Triangle dans rectangle : une lumière neuve sur un problème ancien
Problème connexe avec les travaux de l'ingénieur allemand Walter Porstmann, qui a établi en 1922 le rapport de la longueur à la largeur de la feuille A4 à 
.
Fiche professeur
Ce problème ouvert peut faire l'objet d'une activité réalisable en première S ou en terminale S, après le cours sur l'étude des fonctions, y compris la composée de fonctions.
TICE : utiliser un logiciel de géométrie dynamique pour émettre des conjectures, car la solution mathématique n'est ni directe, ni évidente.
En une séance d'une heure, les élèves construisent la figure avec GéoPlan. Le logiciel leur permet d'émettre des conjectures. Les plus rapides construisent la représentation graphique de la fonction.
La suite est donnée en devoir maison pour la semaine suivante.
Exercice
Triangle inscrit dans un rectangle
National
Soit ABCD une feuille de papier rectangulaire de largeur AB = 4 et de longueur BC = 6. Soit R un point de [AB] (bord inférieur de la feuille) et T un point de [AD] (bord droit de la feuille). On replie la feuille suivant le segment [RT] et on appelle S la nouvelle position du point A (coin inférieur droit de la feuille).
Voir figure ci-dessous.
Dans tout l'exercice, on s'intéresse au cas où S est sur le segment [BC] (bord gauche de la feuille).
On se propose de déterminer s'il existe une position de S sur le segment [BC] qui donne une longueur de pli RT minimale, puis dans un deuxième temps de déterminer s'il existe une position de S sur le s
On pose AR = x, AT = y.
1°) Trouver les valeurs minimale et maximale de x.
2°) Trouver une relation entre x et y lorsque S se déplace sur [BC].
3°) Trouver la valeur de x pour laquelle l'aire de la partie repliée (triangle SRT) est minimale.
Quelle est alors la nature du triangle AST ?
Approche GéoPlan
Placer un point libre R sur le segment [AB]. Si R est à gauche du milieu de [AB] le cercle de centre R passant par A coupe le segment [BC] en S. La médiatrice de [AS] coupe la droite (AD) en T. Si T appartient au segment [AD] le triangle RST représente le bord replié de la feuille. Dans le cadre de droite de la figure ci-dessus on place les points M(x, y) et N(x, z) où z = A(x) est l'aire du triangle SRT.
Figure 1
T hors de [AD]
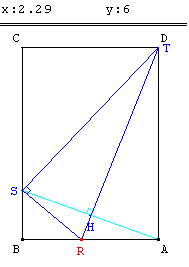
Figure 2
x minimum
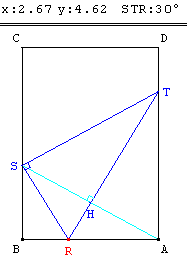
Figure 3
Aire(RST) minimale
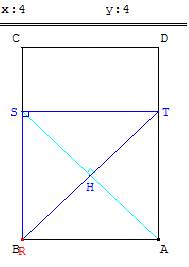
Figure 4
x = 4 : maximum
En déplaçant le point R de A vers B on s'aperçoit :
– que la partie repliée de la feuille est un trapèze qui ne convient pas si 2 < x < 2,29 (figure 1),
– qu'environ 2,29 est la plus petite valeur de x obtenue lorsque T est D (figure 2),
– que l'aire de SRT décroît jusqu'à ce que x atteigne 2,67,
pour x ≈ 2,67 le triangle AST semble être équilatéral avec BS ≈ 
AT (figure 3),
– qu'enfin l'aire croit jusqu'à 8 lorsque le point R est en B pour le maximum 4 de x (figure 4).
Indications
1°) La plus petite valeur de x respectant les conditions est obtenue lorsque T est D (figure 2).
Alors DS = DA = 6, comme CD = 4, d'après Pythagore dans le triangle rectangle CDS, CS = 2
.
Donc, BS = 6 - 2. Or RS = AR = x et BR = 4 - x. D'après Pythagore dans le triangle rectangle BRS :
x2 = (6 - 2)2 + (4 - x)2, soit (6 - 2)2 + 16 - 8x = 0 et enfin x = 9 - 3.
Le maximum pour x est de 4 (figure 4) ; x est compris entre 9 - 3 et 4.
2°) Les triangles rectangles SRT et ART sont symétriques : AR = RS = x, AT = ST = y ; (RT) est la médiatrice de [AS].
Dans le triangle BRS rectangle en B, RS = x et BR = 4 – x donc BS2 = x2 – (4 – x)2 = 8x -16, BS = 2 
.
Les triangles rectangles BAS et ATR ayant leurs côtés perpendiculaires sont semblables et les angles aigus BÂS et ATR sont égaux.
tan(BÂS) = 
= 
et tan(ATR) = 
= 
, donc y = 
3°) L'aire du triangle SRT mesure A(x) = SR × ST / 2 = 
= 
, x variant sur I[9 - 3, 4].
Cette fonction a pour dérivée A’(x) = 
qui est du signe de 3x - 8 sur I.
L'aire A admet un minimum atteint pour x = 
et y = 
; minimum égal à A() = 
tan ATR = = 
; l'angle ATR est alors de 30°. ATS mesure 60° et AT = ST = y ; le triangle isocèle AST ayant un angle de 60° a tous ses angles égaux à 60° et est un triangle équilatéral.
Voir : minimum-maximum
4. Mise en boite
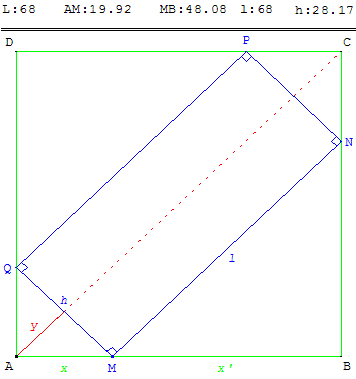
Amiens
Un objet a la forme d'un parallélépipède rectangle de base carrée de côté
a = 68 cm et de hauteur inconnue. Il est vendu conditionné dans une boîte cubique de côté a = 68 cm dont il épouse la forme.
Alors qu'on l'insère dans la boîte, l'objet reste coincé en position inclinée, la boîte ferme quand même, l'arête supérieure affleurant juste le couvercle.
Quelle est la hauteur de l'objet ?
Indications
La « vue de face » d'une perspective cavalière de la figure permet de transformer ce problème en problème plan.
On peut se placer a priori dans le cas particulier où l'objet est centré sur la diagonale de la face, ce qui donne la figure suivante :
La diagonale AC du carré a pour longueur a
= 2y + l = 2y + a, donc 2y = a - a = a( - 1).
Ensuite on constate que d'après la symétrie de la figure, le triangle AMQ dans le coin inférieur gauche est un demi-carré, par conséquent h = 2y.
La hauteur de l'objet vaut donc h = 68( - 1) ≈ 28,17 cm.
Deux variantes : voir la page rectangle dans un rectangle
Multiplication de l'aire d'un triangle
Voir triangle en seconde
Corse
Partage de l'angle d'un triangle en 4
Voir construction de-ci, de-là
Dijon
Existe-t-il un triangle ABC tel que la hauteur issue de A, la bissectrice de l'angle BÂC et la médiane relative au côté [BC] partagent l'angle BÂC en quatre angles de même mesure ?
Carré d'aire cinq fois plus petite
Solution avec le produit scalaire
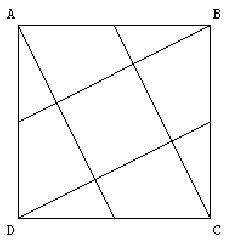
ABCD est un carré de côté 1. À partir de du milieu des côtés de ce carré ABCD, on construit la figure ci-dessous.
1) Justifier que l'on a construit un petit carré à l'intérieur du carré ABCD. Quelle est la longueur de son côté ?
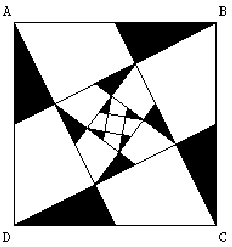
2) Dans la suite, on procède au même découpage des carrés ainsi construits et à chaque étape on colorie les quatre petits triangles formés, comme indiqué sur la figure ci-dessous.
Montrer que l'aire de la partie colorée tend vers un quart de l'aire du carré ABCD, lorsqu'on poursuit indéfiniment cette construction.
Partage en deux d'un triangle
Montpellier
ABC est un triangle quelconque.
I est un point du segment [AC].
Déterminer puis construire le ou les points J de (BC) tels que la droite (IJ) partage le triangle en deux parties de même aire.
Problème équivalent posé à Créteil en 2008.
Octaèdre régulier
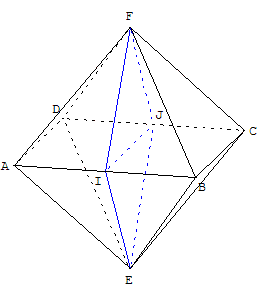
Orléans-Tours
Deux pyramides, de même base carrée ABCD, de sommets respectifs E et F distincts, sont accolées par leur base et forment un octaèdre régulier, c'est-à-dire un solide formé de huit faces identiques qui sont des triangles équilatéraux. On suppose que AB = 1.
Montrer que les faces ABE et CDF sont parallèles et déterminer leur distance, c'est-à-dire la plus courte distance d'un point du plan ABE à un point du plan CDF.
Solution
En notant I et J les milieux respectifs des segments [AB] et [CD], les segments [EI], [EJ], [FI] et [FJ] sont alors des hauteurs d'un triangle équilatéral de côté 1 : ils mesurent tous
. Par suite, EIFJ est un losange.
Il en résulte que les droites sécantes (AB) et (EI) du plan (ABE) sont respectivement parallèles aux droites (CD) et (FJ) du plan (CDF) : ces deux plans sont donc parallèles.
Puisque le losange EIFJ est dans le plan médiateur des segments [AB] et [CD], la distance entre les deux plans (ABE) et (CDF) est aussi la hauteur h du losange.
Or les diagonales du losange EIFJ mesurent IJ = 1 et EF = (c'est la diagonale du carré ACF) :
le losange a donc pour aire A = EF × IJ = EI × h ce qui donne h = 
.
Deux cercles tangents, tangents à un carré : voir minimum-maximum
Table des matières
Google friendly
Faire de la géométrie dynamique en 1ère S
Page no 83, créée le 31/5/2005
mise à jour le 2/11/2009