René Descartes Descartes et les Mathématiques

Rectangle variable inscrit dans un triangle rectangle

Confronter les élèves de seconde à des situations permettant d'expérimenter en mathématiques pour une préparation à l'épreuve pratique du bac S.

Approche intuitive des notions de fonction et de courbe représentative.
Notion d'extremum d'une fonction.
Résolution d'équation avec un logiciel de géométrie dynamique ou par le calcul.

Sommaire

1. Aire maximale d'un rectangle inscrit dans un triangle

2. Distance minimale dans un triangle

3. Orthogonalité dans un triangle

4. Carré inscrit dans un triangle rectangle

5. Carré inscrit dans un quadrilatère

Transformation par barycentres de figures semblables

Voir carré inscrit dans un triangle

1. Aire maximale d'un rectangle

Aire maximale d'un rectangle inscrit dans un triangle rectangle

Classes de troisième et seconde

Maximiser l'aire d'un rectangle dans un triangle

La situation initiale :
Un paysan possède un terrain qui a pour forme un triangle rectangle ABC, rectangle en A, avec AB = 5 hm et AC = 3 hm. Une nouvelle loi oblige notre paysan à travailler dans un champ de forme rectangulaire. Comme le paysan a construit sa grange contenant ses machines en A, il souhaite que A appartienne au champ. Enfin, pour des raisons économiques évidentes, notre paysan souhaite que son champ ait l'aire la plus grande possible. Pouvez-vous l'aider ?

Rectangle d'aire maximale

ABC est un triangle rectangle en A.

Le point M est un point mobile sur le segment [BC]. On appelle N et P les projetés orthogonaux de M respectivement sur les segments [AB] et [AC].
On veut déterminer pour quelle position de M l'aire du rectangle ANMP, inscrit dans le triangle ABC, est maximale.

Télécharger la figure GéoPlan max_aire.g2w

Étude de fonction

Aire d'un rectangle inscrit dans un triangle rectangle

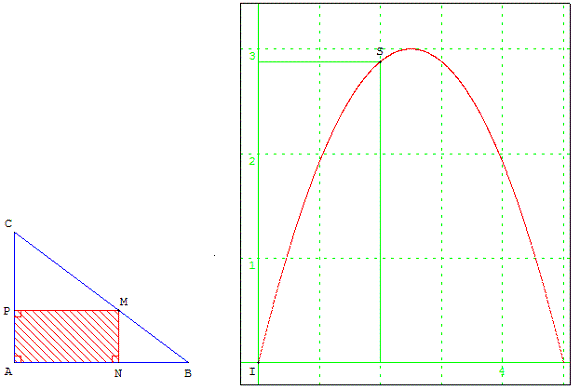
Technique GéoPlan

Dans les deux premiers exercices de cette page est utilisée une seule figure avec deux cadres : le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction.

Pour calculer, avec GéoPlan, l'aire du rectangle ANMP, calculer l'aire du triangle ANP et la doubler.

Commandes
Déplacer le point M avec la souris.
Touches :
T : garder la Trace du point S lorsque M varie,
S : sortie du mode trace et effacement de la trace,
L : dessiner ou effacer la parabole.

Solution

Le maximum est atteint pour x = 2,5. Les points M, N et P sont alors les milieux des côtés du triangle ABC.

Autres données : Il est possible de modifier les positions de A, B ou C en restant dans le cadre de gauche ; ne pas choisir un triangle rectangle trop grand.
Voir aussi la page analyse en 1L

Variante : Étude, lorsque M est variable sur le « quart de cercle » situé sur le cercle de centre O, passant par B ; voir la page maximum-minimum

Démonstration par l'étude d'une fonction

Dans le cas général, elle comporte trop de paramètres et nous semble donc hors de portée d'un élève moyen de seconde et même difficile à envisager en première.
En demandant la démonstration dans un cas particulier simple, on n'enlève pas l'intérêt de l'activité.
On peut prendre par exemple AB = 4 et AC = 3.
En posant BM = x, l'aire f(x) du rectangle ANMP est une fonction du second degré.
On dispose donc des méthodes classiques en seconde par factorisation de f(x) – m (où m est le maximum conjecturé),
ou en 1^re S avec l'utilisation de la dérivée ou des propriétés des fonctions trinômes.

Démonstration géométrique

rectangle inscrit dans un triangle - aire maximale - copyright Patrice Debart 2008

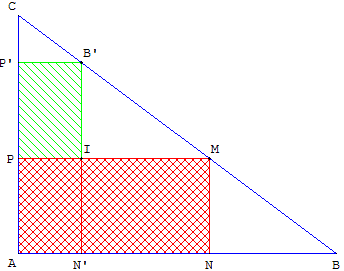
Si M est placé au milieu de [BC], il est clair que l'aire de ANMP vaut la moitié de l'aire du triangle ABC (tracer la médiane [AM] au besoin).

Si M n'est pas au milieu de [BC], on peut montrer que l'aire de AMNP est inférieure à la moitié de l'aire du triangle ABC.

Voir la figure ci-contre dans le cas où M est plus près de B que de C : on trace le symétrique B’ de B par rapport à M.

L'aire de ANMP se décompose en l'aire des rectangles N’NMI et AN’IP.

L'aire de N’NMI est la moitié de l'aire du triangle N’BB’,
comme AP = PP’, l'aire du rectangle AN’IP, égale à l'aire de PIB’P’, est la moitié de l'aire du rectangle AN’B’P’.

L'aire de ANMP, moitié de l'aire du trapèze ABB’P’, est moindre que la moitié de l'aire du triangle ABC.

Télécharger la figure GéoPlan max_aire_triangle_demo.g2w

Voir aussi : le plus grand rectangle inscrit dans un triangle isocèle

Variante : déterminer le point M tel que ANMP soit un carré ; solution : carré inscrit dans un triangle rectangle.

2. Distance minimale dans un triangle

Classes de quatrième, troisième ou seconde

Compétences
– Connaître le rectangle et ses propriétés relatives aux diagonales.
– Savoir que d'un point donné, le point d'une droite le plus proche est le pied de la perpendiculaire menée de ce point à la droite.

Énoncé
ABC est un triangle rectangle en A.
M est un point mobile de l'hypoténuse [BC].
N et P sont les projetés orthogonaux respectifs de M sur les côtés [AB] et [AC].

On veut déterminer, sur [BC], un point M tel que la distance NP soit minimale. Est-il unique ?
Dans ce cas, comment doit être le triangle ABC pour que le segment [NP] soit parallèle à (BC) ?

Indications
Pour ce problème, on peut faire une recherche en classe de seconde dans un cadre analytique, ci-dessous, ou plus bas, le résoudre dans un cadre purement géométrique.

rectangle inscrit dans un triangle - distance minimale - copyright Patrice Debart 2008

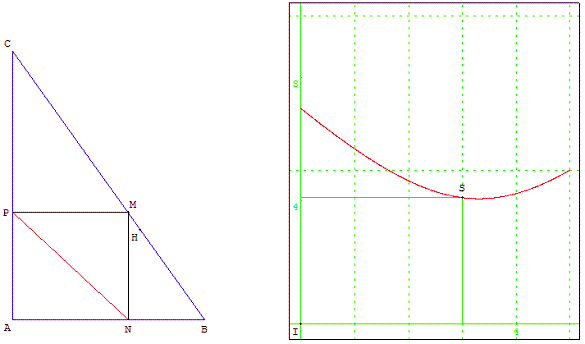
Télécharger la figure GéoPlan dist_mini_triangle.g2w

Conjecture

Pour que la longueur NP soit minimale, il faut que M soit le pied de la hauteur issue de A du triangle ABC.

Le triangle ABC doit être rectangle isocèle pour que le segment [NP] soit parallèle à (BC).

Démonstration géométrique

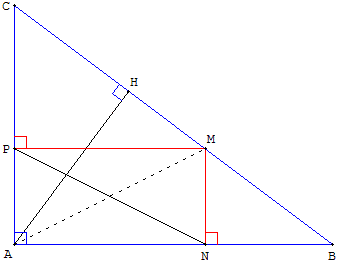
Les diagonales du rectangle ANMP sont de même longueur : NP = AM.
Soit H le pied de la hauteur issue de A. Le triangle AMH est rectangle, AM en est l'hypoténuse. Si M est distinct de H, l'hypoténuse AM est plus grande que le côté AH de l'angle droit.

Télécharger la figure GéoPlan dist_mini.g2w

3. Orthogonalité dans un triangle rectangle

Projections de la hauteur et médiane d'un triangle rectangle.

Soit ABC un triangle rectangle en A.
Le point M est un point mobile sur le segment [BC].
On appelle N et P les projetés orthogonaux de M respectivement sur les segments [AB] et [AC].
Soit I le milieu de [BC].

On cherche à déterminer s'il existe une position du point M telle que les droites (AI) et (PN) soient perpendiculaires.

3.a. Conjecture

rectangle inscrit dans un triangle - orthogonalité - copyright Patrice Debart 2008

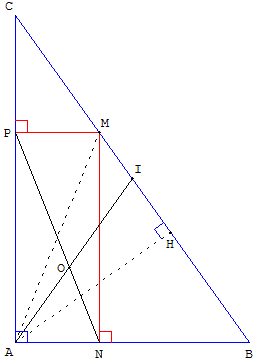
En étudiant plusieurs cas de figure, conjecturer la position du point M telle que (AI) et (PN) soient perpendiculaires :

on pourra faire afficher les angles NOI et AMC (O étant le point d'intersection des droites (AI) et (PN) ) et faire varier ce que l'on peut faire varier.

Démontrer la conjecture.

Télécharger la figure GéoPlan orthogonalite_triangle.g2w

3.b. Démonstration par des calculs d'angles

rectangle inscrit dans un triangle - démonstration par les angles - copyright Patrice Debart 2008

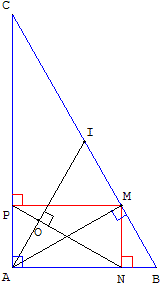
Somme des angles d'un triangle égale à 180°, angles alternes internes, complémentaires…

Dans le triangle ABC, placer M au pied de la hauteur issue de A puis montrer que les droites (AI) et (PN) sont perpendiculaires en suivant la démarche suivante :

On pourra noter α l'angle IÂB. Par la suite, tous les angles seront exprimés en fonction de α.

La médiane AI du triangle ABC est égale à la moitié de l'hypoténuse BC ; les triangles IAB et IAC sont isocèles,
d'où : AÎB = π - 2α, AÎC = 2α, ICA = CÂI = - α.
IÂM = - AÎM = - (π - 2α) = 2α - .
PÂM = CÂI + IÂM = ( - α) + (2α - ) = α.

Par symétrie dans le rectangle APMN, APN = α.
Dans le triangle rectangle APN, on a ANP = - α.
Les angles du triangle AON sont α et - α.
Le troisième angle AÔN est .
Le triangle AON est rectangle, les droites (AI) et (PN) sont perpendiculaires

Télécharger la figure GéoPlan orthogonalite_triangle_2.g2w

3.c. Relations de parallélisme et d'orthogonalité

rectangle inscrit dans un triangle - démonstration géométrique - copyright Patrice Debart 2008

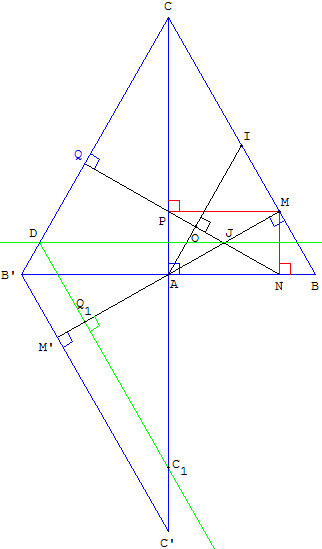
Démonstration par des relations de parallélisme et d'orthogonalité

Utilisation des propriétés des symétries, du théorème des milieux dans un triangle.
Cette méthode exige des constructions auxiliaires sur la figure.

Soit B’, C’ et M’ les images de B, C et M par la symétrie de centre A.

Les droites symétriques (B’C) et (B’C’) font un angle α avec la droite (AB).

La droite (MM’) est perpendiculaire aux droites parallèles (BC) et (B’C’).

Soit J le centre du triangle ANMP et (d) la droite parallèle à (AB) passant par J.

La droite (d) coupe (B’C) en D.
La symétrie par rapport à (d) transforme C en C₁, la droite (DC) en (DC₁), la droite (MA) en (NP).
La droite (DC₁) est parallèle à (B’C’) et fait un angle α avec la droite (d). (MM’) perpendiculaire à (B’C’) est donc perpendiculaire à sa parallèle (DC₁).

Avec le point Q intersection des droites (NP) et (B’C), la symétrie transforme l'angle droit DQ₁A en DQP.
(NP) est perpendiculaire à (B’C).

(IA), droite des milieux du triangle BB’C, parallèle à (B’C) est bien perpendiculaire à (NP).

Télécharger la figure GéoPlan orthogonalite_triangle_3.g2w

3.d. Démonstration avec le produit scalaire

Classe de 1^ère S

Voir : hauteur et médiane d'un triangle rectangle

4. Carré inscrit dans un triangle rectangle

carré inscrit dans un triangle rectangle - figure Geogebra - copyright Patrice Debart 2008

Carré ayant deux sommets sur l'hypoténuse

Construction de Bezout

Étant donné deux points A et B, on place un point C sur le demi-cercle de diamètre [AB]. Le triangle ABC est rectangle en C.

De même que pour un triangle quelconque, construire un carré ABHI, de côté l'hypoténuse [AB] et utiliser une homothétie de centre C pour trouver le côté [DE] du petit carré DEFG inscrit dans le triangle ABC rectangle en C.

Figure interactive dans GeoGebraTube : carré inscrit dans un triangle rectangle

Carré inscrit dans l'angle droit du triangle

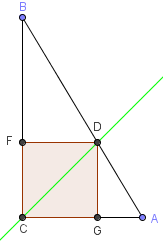
Étant donné deux points A et C, on place un point B sur la perpendiculaire à [AC]. Le triangle ABC est rectangle en C.

La diagonale [AC] du carré CGDF, inscrit dans le triangle rectangle ABC, est la bissectrice de l'angle droit ABC.

Le sommet D est l'intersection de la bissectrice avec l'hypoténuse.

Figure interactive dans GeoGebraTube : carré dans l'angle droit d'un triangle

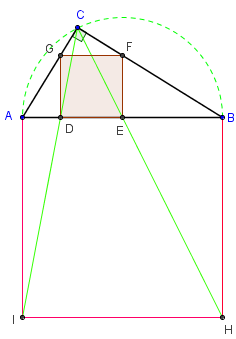
5. Carré inscrit dans un quadrilatère

carré inscrit dans un quadrilatère - recherche - copyright Patrice Debart 2008

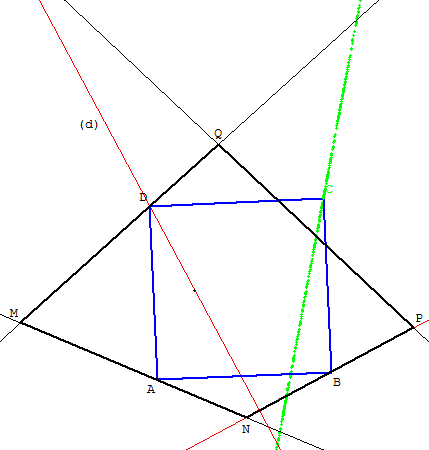
Soit MNPQ un quadrilatère.

Trouver un carré ABCD (direct) inscrit dans ce quadrilatère.

Recherche

Placer un point A sur la droite (MN).

Soit un carré de sommet A, ayant un deuxième sommet B sur le côté (NP).
Le quatrième sommet de ce carré est situé sur la droite (d) image de (NP) par la rotation de centre A et d'angle 90°. Si cette droite coupe la droite (QM) en un point D, soit B son image réciproque, image de D par la rotation de centre A et d'angle – 90°.
A, B et D sont trois sommets d'un carré situés sur trois des côtés du quadrilatère.

Télécharger la figure GéoPlan carre_ds_quadri.g2w

Conjecture

En déplaçant le point A, on peut penser que le lieu géométrique du quatrième sommet C du carré ABCD est situé sur une droite (d’).

Démonstration avec les barycentres

Jean-Paul BEGUIER – Lycée Georges-Brassens – Sainte Clotilde – La Réunion

Transformation par barycentres de figures semblables

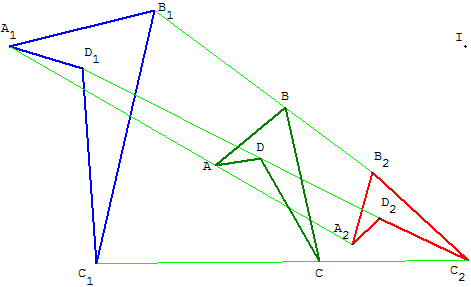
Soit F₁ et F₂ deux figures directement semblables formées des points A₁, B₁, C₁… pour F₁ et des points A₂, B₂, C₂… pour F₂.

Soit un point A de la droite (A₁A₂).
On définit alors le réel t tel que = t .
Les points B, C… partagent les segments [B₁B₂], [C₁C₂]… dans le même rapport que A partage [A₁A₂].
On a donc = t , = t , = t …

La figure F formée par les points ABC… est alors une figure semblable aux deux précédentes.

Remarque : A est le barycentre de (A₁, t-1) ; (A₂, t).
B est le barycentre de (B₁, t-1) ; (B₂, t)…

Ce théorème se montre facilement en utilisant la forme complexe des similitudes.

Avec GéoPlan, définir t comme l'abscisse du point A sur la droite repérée par les deux points A₁, A₂.

Le point B est le point repéré par l'abscisse t sur la droite munie des deux points B₁, B₂. De même pour C, D…

Télécharger la figure GéoPlan figures_semblables.g2w

Solution

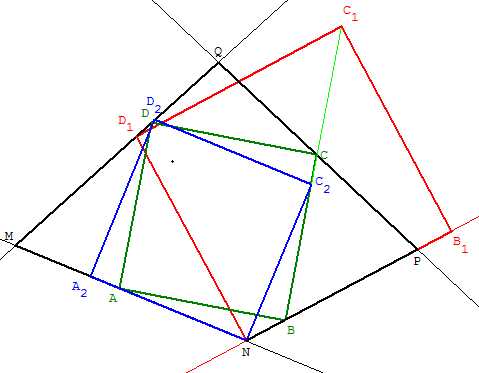
Avec les notations de la figure ci-dessus, on trace les carrés NB₁C₁D₁ et A₂NC₂D₂ avec A₂ sur (MN), B₁ sur (NP), D₁ et D₂ sur (QM).
La position de C sur (C₁C₂) permet de trouver les sommets A, B et D du carré semblable ABCD, solution du problème.