Descartes et les Mathématiques

Triangle inscrit dans un carré

Comment calculer l'aire d'un triangle à l'intérieur d' un carré ?
Des situations de recherche, menant à des calculs d'aires, à optimiser avec la géométrie dynamique.

Sommaire

1. Triangle inscrit dans un carré

2. Triangle équilatéral inscrit dans un carré (un sommet en commun)
    a. Le triangle d'Abul-Wafa
    b. Solution du problème d'Abul-Wafa
    c. Trois triangles équilatéraux
    d. Rotation de centre C et d'angle 60°

    e. Deux triangles équilatéraux dans un carré

    f. Circonscrire un carré à un triangle équilatéral

    g. Calculs d'aires : triangle équilatéral inscrit dans un rectangle

3. Triangle équilatéral inscrit dans un carré
        (les sommets du triangle sur trois des côtés du carré)
    a. Cas particuliers
    b. Recherche menant à une rotation
    c. Aires maximale ou minimale
    d. Lieu géométrique du centre du triangle

Parmi les problèmes de géométrie rencontrés par les artisans et artistes depuis l'Antiquité, figurent en particulier des problèmes « d'inscription » ou de « circonscription ».
On les retrouve chez les géomètres grecs de l'Antiquité ou les mathématiciens chinois bien avant notre ère.

On les trouve aussi chez les artisans arabes pour construire des fresques (comme dans l'Alhambra de Grenade)
ce qui a conduit Abul Wafa à écrire un ouvrage intitulé « Livre sur ce qui est nécessaire à l'artisan en science de la géométrie ».
dans lequel il donne des moyens de construire des figures en particulier inscrites ou circonscrites à d’autres figures.
Certaines constructions sont mathématiquement exactes, d’autres sont des constructions approchées.

Dominique Gaud - IREM de Poitiers - Petit x n^o 79 - 2009

Comment calculer l'aire d'un triangle inscrit dans un carré ?

En général, il n'y a pas de méthode particulière, il suffit de calculer l'aire du triangle !
Dans cette page on trouvera deux problèmes d'optimisation : quand cette aire est-elle maximale ?

1. Aire d'un triangle inscrit dans un carré

Aire maximale d'un triangle dans un carré

Calculer l'aire du plus grand triangle que l'on puisse inscrire dans un carré de côté 1 ?

Il semble difficile de trouver mieux que , qui est l'aire du triangle formé par deux côtés du carré et une diagonale.

Télécharger la figure GéoPlan tri_ds_carre.g2w

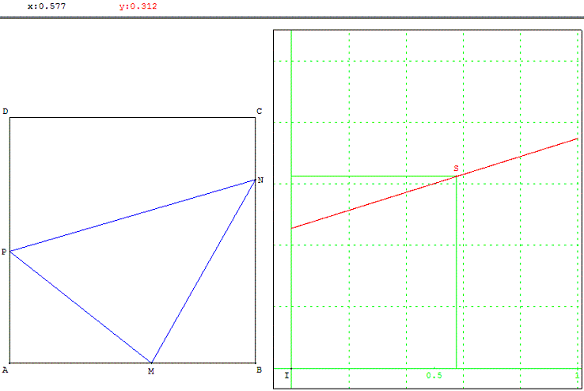
En effet, les points N et P étant fixés sur deux des côtés du carré, comme dans cette figure,
en faisant varier le point M sur le côté [AB], la représentation graphique montre que l'aire est maximale
lorsque M est situé en un des sommets du carré, en B comme ci-dessus,
lorsque AP < BN.

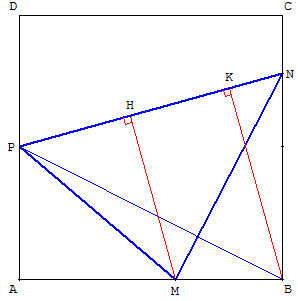
En effet, si [MH] est la hauteur de PNM et [BK] est la hauteur de PNB, MH < BK :
Aire(PNM) < Aire(PNB).
Dans cette configuration, le triangle PNB ayant un sommet dans un coin du carré est le plus grand triangle de côté [PN].

Commande GéoPlan

Touche H : le triangle MNP a une aire inférieure à celle de BNP.

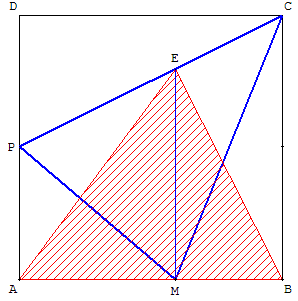
Fixons un des sommets du triangle en C et étudions l'aire du triangle MPC.

La parallèle à (BC) passant par M coupe [PC] en E.

Étudions les triangles de base [ME].
Les triangles AME et PME ont même hauteur AM,
donc Aire(PME) = Aire(AME).

Les triangles BME et CME ont même hauteur MB,
donc Aire(CME) = Aire(BME).

D'où Aire(PME) + Aire(CME) = Aire(AME). + Aire(BME).
Les triangles MPC et ABE ont même aire, aire égale à AB × ME.
Cette aire est maximale lorsque ME, maximal, est égal à BC.

Une aire de , qui est l'aire du triangle ABC, est bien l'aire maximale.

2. Triangle équilatéral inscrit dans un carré

Problème d'Abul Wafa : triangle ayant un sommet en commun avec le carré

Muhammad Abu'l-Wafa (Abul Wafa) est un mathématicien et astronome persan connu pour ses apports en trigonométrie et pour ses constructions à la « règle et au compas ».
Il est né en 940 à Buzjan dans la région de Khorasan. À l'âge de vingt ans, il part pour Bagdad où il restera jusqu'à sa mort en 998.

2.a. Le triangle d'Abu'l-Wafa

Classe de première L

Étant donné un carré OPCQ, construire un triangle équilatéral CIJ, I et J étant situés sur les côtés du carré.

Abul Wafa se posait le problème comme suit :
soit OPCQ un carré de centre O₂, et un point quelconque I sur l'arête [OP] et J le point symétrique de I par rapport à la droite (OC) ; J est alors sur [OQ].
Le triangle CIJ peut-il être équilatéral ?

La construction n'est pas unique, il s'agit d'en réaliser au moins une, aboutissant à un triangle équilatéral inscrit dans le carré.

2.b. Solutions proposées par Abul Wafa

Solutons exacte ou approchée ?

Construction approchée

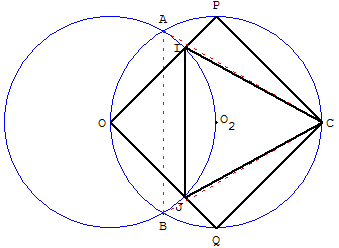
1. Construire le cercle (c₂) de centre O₂, circonscrit à OPCQ.
2. Construire un second cercle (c₁) de centre O, passant par O₂.
3. Nommer I et J les points d'intersection du cercle (c₁) avec les côtés [OP] et [OQ] du carré.

Le triangle CIJ n'est pas équilatéral, mais semble être un tracé acceptable.
Le comparer au triangle équilatéral ABC.

Télécharger la figure GéoPlan care_tri_app.g2w

Multiplication par 3 de l'aire d'un carré : construction d'Abu l-Wafa

Construction « exacte » du triangle d'Abul Wafa

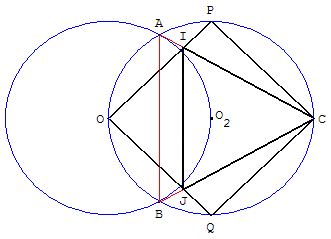
1. Construire le cercle (c₂) de centre O₂, circonscrit à OPCQ.
2. Construire un second cercle (c₁) de centre O, passant par O₂.
3. Nommer A et B les deux points d'intersection de ces cercles
      (le triangle ABC est équilatéral comme le montre la figure cercles et triangle équilatéral).
4. On peut alors prouver que les droites (CA) et (CB) coupent les arêtes du carré en deux points, qui sont les points I et J recherchés.

Le triangle CIJ est équilatéral, comme triangle isocèle ayant un angle ICJ de 60°.

Télécharger la figure GéoPlan care_tri.g2w

2.c. Trois triangles équilatéraux

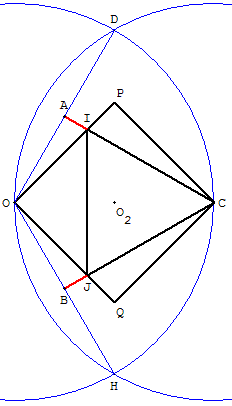
Construction

Construire les cercles (c₁) de centre O, passant par C, et (c₂) de centre C passant par O.
Ces deux cercles se coupent en D et H.
Soit A et B les milieux de [OD] et [OH].
Les droites (CA) et (CB) coupent les arêtes du carré aux points I et J.

Le triangle CIJ est équilatéral.

Indications

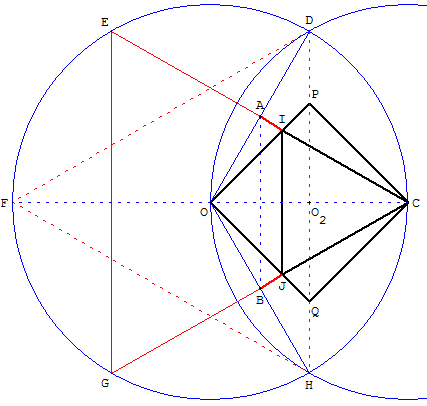
Les rayons [OD] et [OH] font un angle DÔH de 120°. Leurs médiatrices (CA) et (CB) font un angle AÔB de 60°.

En effet, si F est le symétrique de C par rapport à O, le triangle DFH est équilatéral comme le montre la figure des deux cercles.
O est le centre du cercle circonscrit, donc (OD) et (OH) sont deux médiatrices du triangle.

(CA) et (CB) recoupent le cercle (c₁) en E et G.
Le triangle CEG symétrique (par rapport à O) de DFG est aussi équilatéral. (on note que CDEFGH est un hexagone régulier).
Par symétrie par rapport à O, les cordes [CE] et [CG] sont les médiatrices des rayons [OD] et [OH] qu'elles coupent en leurs milieux A et B.

Enfin, on montre que la figure admettant (CF) comme axe de symétrie, le triangle CIJ est isocèle ; donc avec un angle ICJ de 60°, il est équilatéral.

Télécharger la figure GéoPlan care_tri_3.g2w

2.d. Construction à l'aide d'une rotation de centre C et d'angle 60°

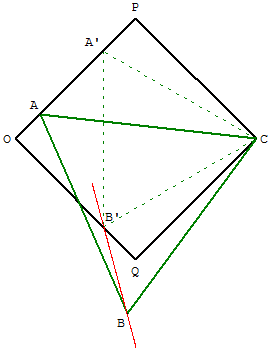
Recherche avec un triangle équilatéral ayant comme sommets le sommet C du carré et un point A variable sur le côté [OP].

Deux des sommets du triangle ne sont pas sur un même côté du carré, sinon le triangle équilatéral serait l'intérieur du carré ;
donc les deux sommets du triangle, autres que C, sont sur les côtés [OP] et [OQ].

Choisissons un point A variable sur le côté [OP] et construisons le point B tel que le triangle CAB soit équilatéral.

En déplaçant le point A, nous trouvons un point A’, tel que le point B soit sur le côté [OQ] en B’.
Le triangle CA’B’ est alors solution du problème.

Nous remarquons que le lieu du point B est un segment de droite, image de [OP] par la rotation de centre C et d'angle 60°.
Le point B’ est situé à l'intersection de cette image avec [OQ].

Télécharger la figure GéoPlan care_tri_4.g2w

Construction

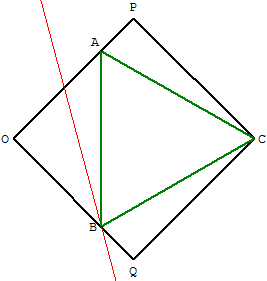
Construire l'image (d) de la droite (OP) par la rotation r de centre C et d'angle 60°, cette droite image (d) coupe (OQ) en B,
puis on obtient le point A en construisant l'image de B par la rotation réciproque r^{– 1} de centre C et d'angle – 60°.

Le triangle ABC, inscrit dans le carré, est équilatéral.

Télécharger la figure GéoPlan care_tri_2.g2w

Démonstration

La droite image (d) coupe bien (OQ) car sinon (d) serait parallèle à (OQ), et donc perpendiculaire à (OP) :
impossible, car l'angle entre (d) et (OP) vaut 60° (ou 120°).
Enfin, ABC est bien équilatéral, car A est l'image de B par la rotation réciproque r^{– 1} de centre C et d'angle – 60° ;
B est sur (d), donc A est bien sur l'image réciproque (OP). Le triangle ABC est donc isocèle en C et d'angle au sommet 60°,
les trois angles du triangle valent chacun 60°.

Application de cette technique au cas où les sommets du triangle équilatéral sont sur trois des côtés du carré

Calculs d'aires

Si le carré a pour côté a = 1, le triangle APC rectangle en P a pour angle en C 15°, le côté AP mesure a tan(15°) = 2 - ≈ 0,27.

AC, côté du triangle équilatéral, mesure ( - 1) ≈ 1,03.
L'aire du triangle APC est 1 - ≈ 0,13.

Le triangle rectangle isocèle OAB a pour petit côté OA = OB = 1 - tan(15°).
Son aire est (1 - tan(15°))²/2 = 2 - ≈ 0,27.

L'aire du triangle OAB est égale à la somme des aires des triangles APC et BQC.
L'aire du triangle ABC est 2 - 3.

2.e. Deux triangles équilatéraux dans un carré

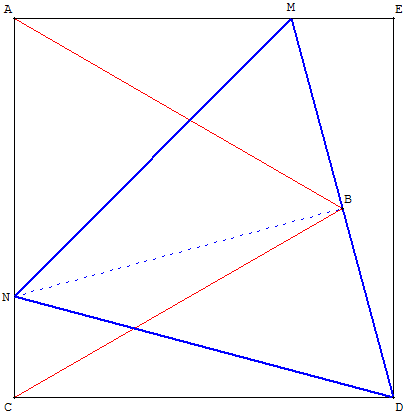
Deux solutions au problème d'Abul Wafa

ABC est un triangle équilatéral à l'intérieur du carré ACDE.
La droite (DB) coupe [AE] en M.

Une première construction

La perpendiculaire en B à (DM) coupe [AC] en N.

Le triangle DMN est équilatéral ?

Télécharger la figure GéoPlan tri_equi_carre_5.g2w

Indication

Le triangle DMN est équilatéral (preuve ci-contre) et son aire est environ 1,035 fois l'aire de ABC.

Avec une symétrie par rapport à une diagonale

Une preuve par une deuxième construction, avec une symétrie par rapport à une diagonale

La symétrie axiale par rapport à la diagonale (AD) transforme M en N.
Le triangle DMN est équilatéral

Démonstration

Par la symétrie, la droite (DM) a pour image (DN) ; le côté (AE) a pour image (AC). Le point N est donc situé sur (AC).
Le segment [DM] a pour image [DN]. DM = DN et le triangle DMN est isocèle en D.

Dans le paragraphe triangle équilatéral à l'intérieur d'un carré, sachant que AEB est un triangle isocèle, on a trouvé que la mesure de l'angle BDE est 15°.

Par la symétrie, l'angle MDE a pour image NDC. Ces deux angles mesurent 15°.
On a donc MDN = EDC - EDM - NDC = 90° - 2 × 15° = 60°.

Le triangle isocèle DMN, ayant un angle de 60°, est équilatéral.

[NB] est la hauteur du triangle équilatéral ce qui valide la construction ci-dessus.

Télécharger la figure GéoPlan tri_equi_carre_6.g2w

2.f. Circonscrire un carré à un triangle équilatéral

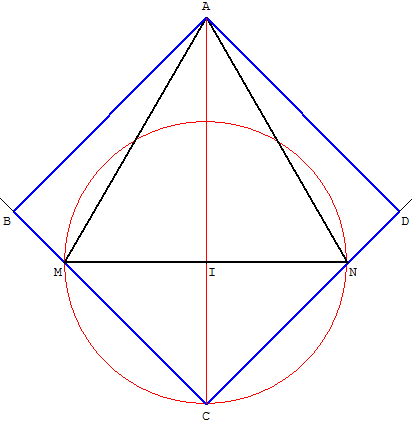
Réciproque par une construction d'Abul Wafa

AMN est un triangle équilatéral et I le milieu de [MN].

Sur la médiatrice (AI) de [MN], à l'extérieur du triangle,
on place le point C tel que IC = IM.

La perpendiculaire à (CM) passant par A coupe (CM) en B,
la perpendiculaire à (CN) passant par A coupe (CN) en D.

ABCD est un carré circonscrit au triangle AMN.

Indications

Las angles en B, C et D de ABCD sont droits, c'est donc un rectangle.

(AC) est axe de symétrie de la figure : CB = CD et on a un carré.

Télécharger la figure GéoPlan tri_equi_carre_rep.g2w

2.g. Exercices de-ci, de-là : Calculs d'aires

487-4. Triangle équilatéral inscrit dans un rectangle

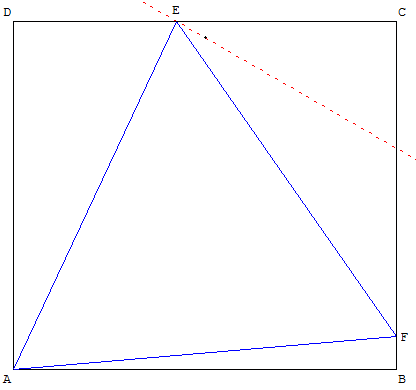
ABCD est un rectangle, AEF un triangle équilatéral où E et F sont sur les côtés [DC] et [CB].

Quelle relation lie les aires des triangles ADE, AFB et ECF ?

Télécharger la figure GéoPlan tr_equi_ds_rectangle.g2w.g2w

Construction

La droite (d), image de (CB) par la rotation de centre A et d'angle 60°, coupe (CD) en E.

Soit F l'image réciproque du point E par la rotation. Si les points E et F sont sur les côtés [DC] et [CB], AEF est le triangle équilatéral cherché.

Les cas limites correspondants aux triangles équilatéraux ayant pour côté un des côtés du rectangle
et la longueur de la hauteur étant égale à l'autre côté, on montre facilement que la condition d'existence de la figure est :

≤ L/l ≤ .

Indication

La somme des aires des triangles ADE et AFB est égale à l'aire du triangle ECF.

Solution de Georges Lion (Wallis)

Posons α = DÂE.
On obtient CEF = + α - = + α et BFA = + α + - = + α.

Notons a la longueur du côté du triangle équilatéral et calculons les aires des trois triangles rectangles le bordant :

4 S(ADE) = 2 a² sin α cos α = a² sin 2α ;

de même S(ECF) = a² sin( + 2α) et 4 S(AFB) = a² sin( + 2α).

4 [S(ADE) + S(AFB)] = a² [sin 2α + sin( + 2α)]. Avec la formule sin 2p + sin 2q = 2 sin(p+q) cos(p-q), on trouve :

4 [S(ADE) + S(AFB)] = a² × 2 sin[α + ( + α)] cos[α − ( + α)] = a² × 2 sin[ + 2α] cos[ − ] = a² sin( + 2α) = 4 S(ECF).

On a donc bien la relation : S(ADE) + S(AFB) = S(ECF).

Exercices du bulletin vert :

Patrice Debart tient quant à lui un site très complet d’activités et exercices en tout genre de la Sixième à la Terminale (!)
proposant entre autres des reprises d’exercices de-ci, de-là. À ne pas rater non plus !

Oméga n^o 9 : la revue de la régionale APMEP de Caen propose des solutions géométriques
ainsi qu'une splendide équidécomposition d'Éric Trotoux à ne pas rater !

3. Triangle équilatéral inscrit dans un carré

Les sommets du triangle sur trois des côtés du carré - Aires maximale ou minimale

Peut-on inscrire un triangle équilatéral dans un carré, pas facile !

En tentant quelques figures, on trouvera les deux exemples ci-dessous en plaçant, comme Abu'l-Wafa,
un sommet du triangle sur un sommet du carré, ou en plaçant un sommet du triangle au milieu d'un côté du carré.

Ensuite, nous ferons une recherche plus générale d'un triangle équilatéral ayant pour sommet un point M donné.

Enfin, en déplaçant un sommet du triangle sur un côté du carré, nous rechercherons quels sont les triangles d'aires maximale ou minimale.

Nous terminerons par une étude du lieu des centres de ces triangles.

3.a. Cas particuliers : Construction d'Abu'l-Wafa

Le triangle MNP, inscrit dans le carré, est équilatéral.
Lorsque M varie sur le côté [AB], on vérifie que l'on a une aire maximale lorsque N ou P sont placés en un des sommets du carré. ...

Pour une aire minimale : point M placé au milieu de [AB].

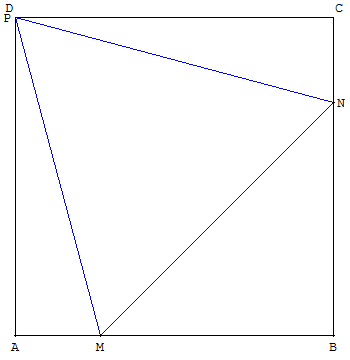
Un sommet du triangle confondu avec un sommet du carré

En effet, dans un carré ABCD de côté 1, si on pose AM = x (0 < x < 1),
alors BM = 1 – x
et dans ce cas particulier CN = x et BN = 1 – x.

Les relations de Pythagore permettent de calculer le carré du côté a du triangle équilatéral :

Dans le triangle rectangle DAM : DM² = a² = 1 + x²,
dans le triangle rectangle isocèle MBN : MN² = a² = 2(1 – x)².

Soit 1 + x² = 2(1 – x)² ou (x – 2)² = 3.
La solution positive de cette équation est x = 2 – ≈ 0,268.

Alors a² = 1 + (2 – )² = 8 – 4 et a = ( – 1) ≈ 1,035 > 1.

L'aire d'un triangle équilatéral de côté a est égale à a².
L'aire est donc de 2 – 3 ≈ 0,464 < .

Télécharger la figure GéoPlan tri_equi_carre_3.g2w

Un sommet du triangle au milieu d'un côté du carré

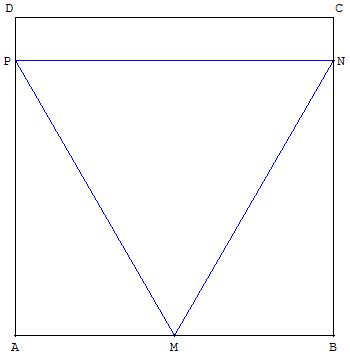
L'aire d'un triangle équilatéral de côté a est égale à a².

Pour AM = x = , le côté est a =1. L'aire est donc de ≈ 0,433.

3.b. Recherche menant à une rotation

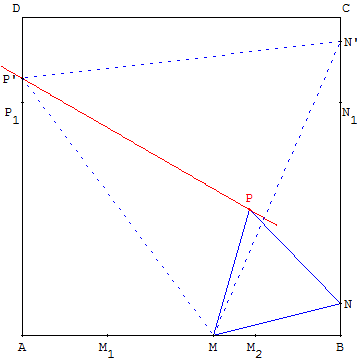
Recherche, plus générale, avec un triangle équilatéral ayant pour sommet un point M donné sur le côté [AB] et un point N variable sur [BC].

Deux des sommets du triangle ne sont pas sur un même côté du carré, sinon le triangle équilatéral serait l'intérieur du carré ;
quatre côtés du carré pour trois sommets du triangle, donc deux sommets sur des côtés consécutifs.

Choisissons un point M donné sur le côté [AB] et un point N variable sur [BC] et construisons le point P tel que le triangle MNP soit équilatéral.

Dans le cas de figure ci-contre, en déplaçant le point N, nous trouvons un point N’, tel que le point P soit sur le côté [CD], en P’.
Le triangle MN’P’ est alors solution du problème.

Nous remarquons que le lieu du point P est un segment de droite, image de [BC] par la rotation de centre M et d'angle 60°.
Le point P’ est situé à l'intersection de cette image avec [AD].

En plaçant sur les côtés du carré, selon la figure, les points M₁, M₂, N₁, P₁ à une distance égale à 2 – des sommets,
nous vérifions, en déplaçant le point M, que pour inscrire un triangle sur trois côtés du carré autres que [CD],
le problème n'a de solution que si M est compris entre M₁ et M₂,
N appartient alors au segment [N₁C] et P au segment [P₁D].

Aux rotations, autour du centre O du carré, près, un raisonnement analogue avec les trois autres côtés permet d'obtenir toutes les solutions.

Télécharger la figure GéoPlan tri_equi_carre_4.g2w

3.c. Aires maximale ou minimale

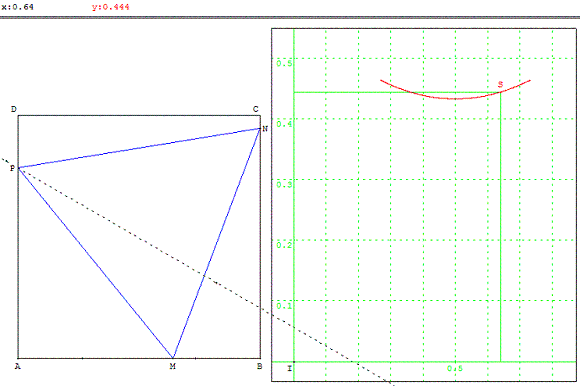
Quelle est l'aire du plus grand triangle équilatéral que l'on puisse inscrire dans un carré de côté 1 ? Du plus petit triangle équilatéral inscrit ?

Soit M un point du côté [AB].

Comme au paragraphe ci-dessus, construire l'image (d) de la droite (BC) par la rotation r de centre M et d'angle 60°,
cette droite image (d) coupe (AD) en P, puis on obtient le point N en construisant l'image de P par la rotation réciproque r^{– 1} de centre M et d'angle – 60°.

Le triangle MNP, inscrit dans le carré, est équilatéral.

Lorsque M varie sur le côté [AB], on vérifie que l'on a une aire maximale lorsque N ou P sont placés en un des sommets du carré.

Voir ci-dessus une des constructions d'un triangle solution, d'aire maximale, pour AM = 2 – avec un angle AMD de 75° ( radians).
Le plus grand triangle équilatéral inscrit dans le carré a donc pour aire 2 – 3 ≈ 0,464.

Le plus petit triangle équilatéral inscrit dans le carré a son sommet M au milieu du côté [AB] du carré. On a AM = ,
et l'aire minimale est ≈ 0,433.

Pour une aire minimale : point M placé au milieu de [AB].

Télécharger la figure GéoPlan tri_equi_carre.g2w

3.d. Lieu géométrique du centre du triangle

Exercices de-ci, de-là 478-2 :
d'après la solution de Robert Boudon - Bulletin APMEP n^o 481

Trouver le lieu géométrique des centres des triangles équilatéraux inscrits dans un carré (de côté 1).

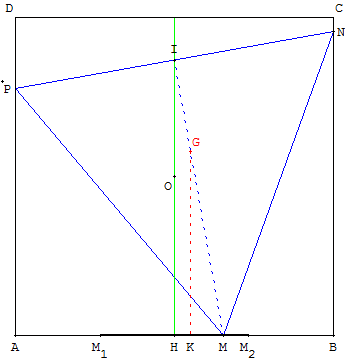
Quatre côtés pour trois sommets du triangle, supposant un côté sans sommet, [DC] par exemple, prenons un sommet M sur le côté [AB] entre M₁ et M₂, points tels que :
AM₁ = BM₂ = 2 − , d'après les calculs du paragraphe précédent.

Le milieu I du côté [NP] est situé sur la médiatrice de [AB] passant par le milieu O du carré.
En déplaçant le point M, on s'aperçoit que le point I est fixe. Pour le démontrer, calculer HI :

Calcul de HI (on trouvera HI = )
Soit t l'angle APM, l'angle DPN est alors le supplémentaire de t + ,
soit DPN = π − − t = − t.
Dans un triangle rectangle ayant pour hypoténuse [PN], de longueur a égale au côté du triangle équilatéral,
et ayant comme côté de l'angle droit, la parallèle à (DC) passant par N, de longueur 1, on a :

1 = PN sin(DPN), soit 1 = a sin( − t) = a sin(t + ).
Dans le triangle rectangle AMP, AP = PM cos(APM) = a cos t.

Par rapport aux côtés parallèles (AD) et (BC), la sécante (PN) découpe des angles internes APN et PNB supplémentaires.
D'où (t + ) + ( + MNB) = π,
soit t + MNB = , donc MNB = − t
Dans le triangle rectangle BNM, BN = MN cos(MNB) = a cos( − t).

AP + BN = a cos t + a cos ( − t) = a sin(t + ) = ,
Les droites (AD), (HI) et (BC) étant des parallèles équidistantes, on a HI = (AP + BN)/2 = .

Lieu du point G

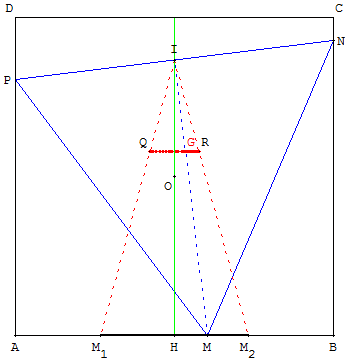
Le centre G du triangle équilatéral est situé aux de la médiane [MI].
D'où KG = HI = , par la propriété de Thalès dans le triangle HIM.

En traçant le lieu du point G, on trouve le segment [QR], image de [M₁M₂] par l'homothétie de centre I et de rapport , segment situé à une distance égale à de [AB].

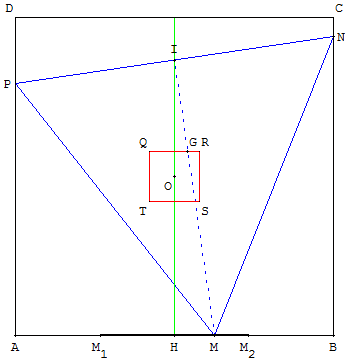
Un raisonnement analogue avec les trois autres côtés permet d'obtenir les mêmes résultats mutatis mutandis.

Le lieu est donc le carré QRST de centre O et de côté de longueur 2 − 1.

Télécharger la figure GéoPlan tri_equi_carre_2.g2w

Table des matières

Dans d'autres pages du site

La géométrie au collège

Rectangle inscrit dans un triangle

Triangle équilatéral à l'intérieur d'un carré au lycée

Carré et deux triangles équilatéraux - Prouver des alignements

Classe de cinquième : un triangle dans un rectangle

Aire d'un triangle inscrit dans un carré

Le plus grand triangle isocèle inscrit dans un cercle

Téléchargement

Télécharger triangle_carre.pdf : ce document au format « .pdf »

Google friendly