Descartes et les Mathématiques

Analyse en 1L avec un logiciel de géométrie dynamique

Cycle terminal de la série littéraire - option facultative - CNDP

Utilisation de deux cadres dans GéoPlan : un pour visualiser une situation géométrique, l'autre pour tracer une fonction.

Sommaire

1. L'ombre d'un gyrophare

2. La plus petite aire

4. Trajet en temps minimum

6. Histoires de toit - voûte circulaire

La parabole en L

3. Aire maximum
    a. d'un rectangle dans un triangle
    b. d'un rectangle dans un trapèze

5. Approche géométrique d'une tangente

6. Histoires de toit - voûte parabolique

7. Quadrature par la méthode d'Archimède

8. Le crible géométrique de Matiiassevitch

Technique GéoPlan : dans certains des exercices est utilisée une seule figure avec deux cadres :
le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction.

1. L'ombre d'un gyrophare

Dans un aérodrome, un gyrophare est placé au-dessus d'un hangar cylindrique de 10 m de haut et de base circulaire de 40 m de diamètre. Le cône d'ombre est un cercle de rayon x et on veut déterminer la hauteur h du gyrophare (au-dessus du sol) en fonction de ce rayon.

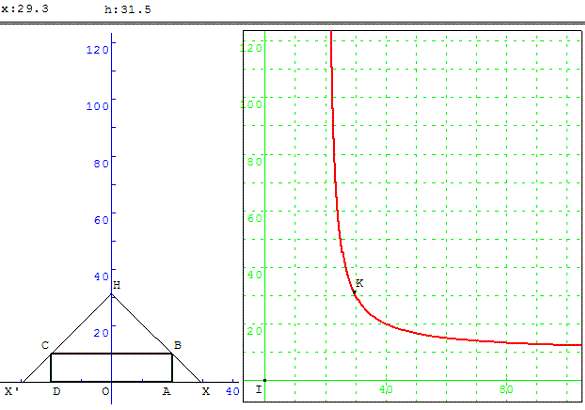
a. Faire le lien entre la situation décrite et le schéma ci-dessus.
b. En considérant les deux triangles semblables XAB et XOH, montrer que h(x) = .
c. En considérant les triangles semblables BIH et XAB, montrer que h(x) = + 10.
d. Vérifier, par le calcul, que les deux expressions sont égales, pour tout x > 20.
e. Établir le tableau de variation de h en fonction de x.

Technique

Dans chacun de mes exemples, déplacer le point variable de la fenêtre de gauche avec la souris.

Télécharger la figure GéoPlan gyrophar.g2w

2. La plus petite aire

Soit un segment [OA] de longueur donnée (par exemple 10) et M un point de ce segment.
Du même côté de [OA], on construit le triangle équilatéral OTM et le carré AMNP. On pose OM = x.

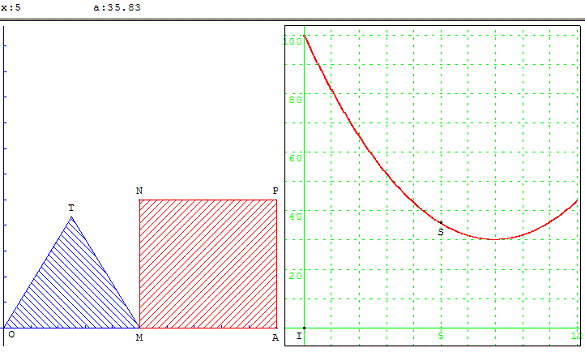
a. Donner l'expression et la représentation graphique de l'aire du triangle OTM en fonction de x.
b. Donner l'expression et la représentation graphique de l'aire du carré AMNP en fonction de x.
c. Étudier les variations de la somme des aires du triangle et du carré en fonction de x.
Pour quelle valeur de x cette aire est-elle minimum ?

Remarque - On peut envisager un triangle OTM rectangle isocèle, ou bien un deuxième carré OMTU.
Cette situation conduit à étudier d'abord deux fonctions trinômes avec des coefficients de x² de signes différents, puis la somme de ces deux fonctions.

Télécharger la figure GéoPlan aire_c_t.g2w

3. Aire maximum

3.a. Aire d'un rectangle inscrit dans un triangle rectangle

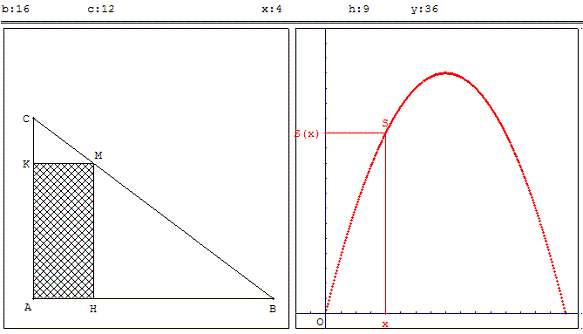
ABC est un triangle rectangle en A. Où doit être situé le point M, sur le côté [BC], pour que l'aire du rectangle AHMK soit maximale ?

Pour cet exemple : AB = 16, AC =12 ; le maximum est trouvé pour x = AH = 8, H, K et M sont alors les milieux des côtés du triangle ABC.

Télécharger la figure GéoPlan fn_cadre.g2w

Autres données : Il est possible de modifier les positions de A, B ou C en restant dans le cadre de gauche ; ne pas choisir un triangle rectangle trop grand.
Voir aussi la page rectangle variable inscrit dans un triangle

Variante : Étude lorsque M est variable sur le « quart de cercle » situé sur le cercle de centre O, passant par B : voir la page maximum-minimum

3.b. Aire maximum d'un rectangle inscrit dans un trapèze rectangle

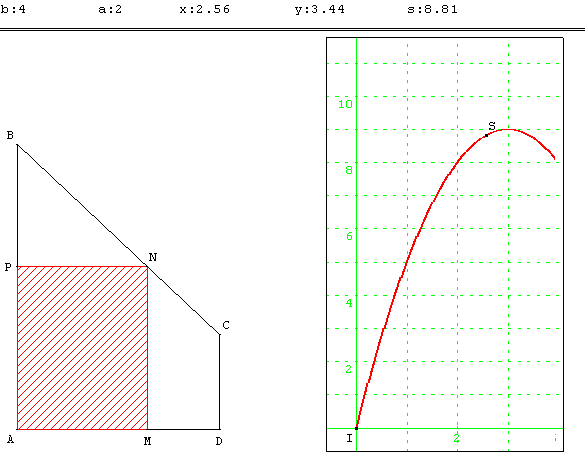
ABCD est un trapèze rectangle en A et D tel que AB = 6 cm, AD = 4 cm et CD = 2 cm.
Un point N parcourt le segment [BC] ; on construit le rectangle AMNP avec P sur [AB] et M sur [AD].
Exprimer l'aire du rectangle AMNP en fonction de AM et représenter graphiquement cette aire en fonction de AM.
Pour quelle valeur de AM cette aire est-elle maximum ?

Remarque - On peut séparer la classe en groupes et faire cet exercice avec différentes valeurs de a et b, (b > a),
avec CD = a, AD = b, AB = a + b, et vérifier alors que le maximum est toujours atteint quand P est au milieu de [AB], puis le démontrer.

Télécharger la figure GéoPlan aire_tra.g2w

4. Trajet en temps minimum

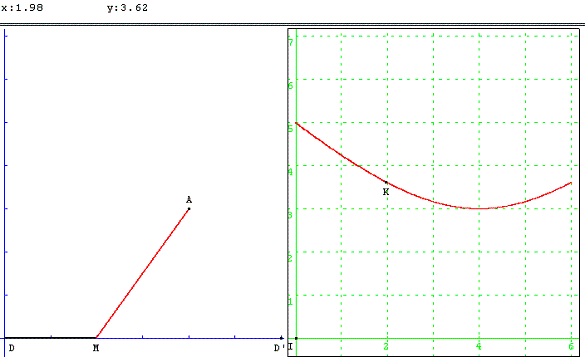
Variations

Un point A se situe à 3 km d'un segment [DD’] de longueur 6 km et sa projection orthogonale sur [DD’] se situe en H à 4 km de D (et à 2 km de D’).
a. Sans aucun calcul, dresser le tableau donnant les variations de la longueur AM en fonction de la longueur DM.
b. Exprimer analytiquement AM en fonction de DM et représenter graphiquement cette fonction sur la calculatrice.

Télécharger la figure GéoPlan parcou1.g2w

Minimum d'un parcours à VTT

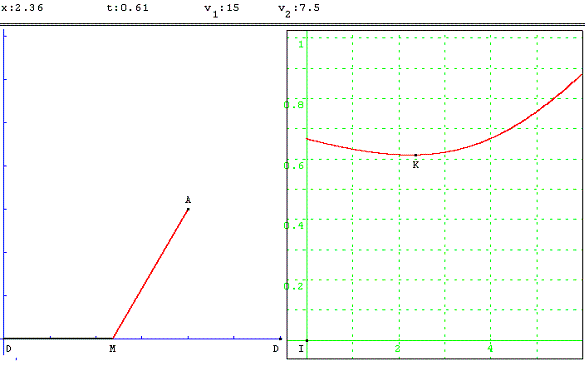
Un vététiste part de D pour arriver en A, situé au milieu d'une grande prairie. Il peut emprunter un chemin carrossable [DD’] rectiligne de 6 km de long.
Le point A est distant de 3 km de [DD’], se projette en H sur (DD’) ; DH = 4 km et HD’ = 2 km.

Quel itinéraire doit-il choisir pour aller le plus rapidement possible de D à A dans les cas suivants ?
a. il se déplace à la même vitesse v (par exemple 15 km.h^{– 1}) sur le chemin et dans la prairie ;
b. il se déplace à la vitesse v₁ sur le chemin, à la vitesse v₂ dans la prairie, et v₁ = 2v₂ (avec par exemple v₂ = 10 km.h^{– 1}).

Indications : si les vitesses v₁ et v₂ sont exprimées en km.h^{– 1} et si on pose DM = x, le temps t (en heure) mis par le vététiste pour aller de D à A vérifie :
t = .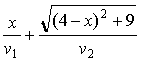

Télécharger la figure GéoPlan parcou2.g2w

Variante avec un bateau ou une voiture : optimisation au CAPES Externe de mathématiques

5. Approche géométrique d'une tangente à la parabole

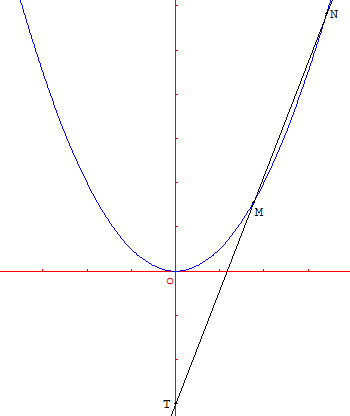
Recherche d'une propriété des tangentes issues d'un point T situé sur l'axe de la parabole.

Première figure

Sécante issue d'un point de l'axe

La courbe (P) d'équation y = ax²
(a désignant un réel non nul, par exemple a = 0,5) est appelée parabole.

Soit T un point de l'axe des ordonnées ayant une ordonnée t de signe contraire à celui de a (par exemple t = − 4). On fait pivoter une droite Δ autour du point T et on observe l'intersection de Δ et (P) : faire des essais
(l'équation de étant de la forme y = mx - 4,
on essaiera avec des valeurs entières de m : 0, 1, 2, 3…).

Télécharger la figure GéoPlan para_tan.g2w

Deuxième figure

Deux tangentes issues d'un point de l'axe

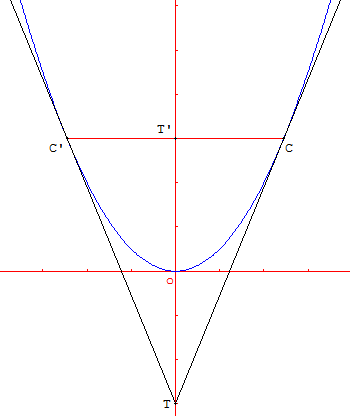
On met ainsi en évidence deux cas où la droite est « tangente » à (P). Le milieu T’ des points de contact C et C’ des deux tangentes à la parabole semble alors lié au point T.
L'objectif est alors de prouver la propriété conjecturée.
Après généralisation, on en déduit un moyen simple pour construire les tangentes à une parabole passant par un point donné de son axe de symétrie.

Télécharger la figure GéoPlan para_tan2.g2w

Indications : on pourra d'abord chercher les abscisses des points d'intersection de (P) et Δ.
Dans les cas m = 3 on aboutit à une équation de la forme (x − 3)² = 1,
puis m = 4…
Pour m quelconque, ces calculs préliminaires amènent à l'équation :
(x − m)² = m² − 8.
Il y a tangence quand il y a une seule solution, donc lorsque m² = 8.

On peut séparer la classe en groupes et faire cet exercice avec différentes valeurs de t (voire de a). Chaque groupe aboutit (?) au même résultat : le point T’ est symétrique de T par rapport à O.

Remarque : on ne manquera pas par la suite de vérifier que l'on obtient bien la même tangente en utilisant la dérivée.

Voir : tangente en 1^ère S

6. Histoires de toit

Toit sur une voûte circulaire

Un toit s'appuie sur une voûte en demi-cercle de rayon r, de diamètre [AA’], comme l'indique la figure ci-dessous.

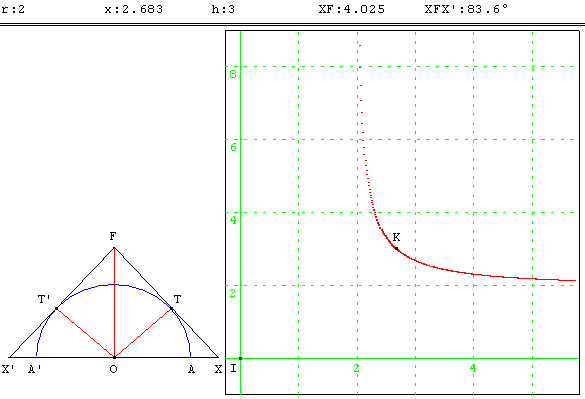
Le toit de sommet F est représenté par les segments [XF] et [X’F] tangents en T et T’ au cercle. Soit h l'ordonnée de F et x l'abscisse de l'extrémité X ;
les coordonnées des sommets sont alors F(0, h), X(x, 0) et X’(− x, 0).

6.a. Quelle doit être la hauteur h du faîte F pour que les deux pans du toit forment un angle droit ? Situer le point de contact de chaque pans avec la voûte.

Par des simples considérations géométriques, on trouve h = x = r et les coordonnées de T sont (r, r).

Remarque : on peut reprendre ces questions dans le cas d'un toit formant un angle de 60° ou 120°.

6.b. Plus généralement déterminer l'expression donnant la hauteur h en fonction de la longueur OX notée x.

Construire une représentation graphique de la fonction x → h.

L'expression de h en fonction de x s'obtient assez facilement en considérant les triangles rectangles semblables FTO et OTX.

On trouve h = .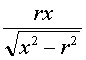

Bien que ce type de fonction soit en dehors du programme de terminale L, la calculatrice permet une représentation graphique « aisée » ; celle-ci peut aussi se construire point par point à partir du dessin ; l'utilisation d'un logiciel de géométrie dynamique sera bienvenue (le dessin met en évidence deux droites asymptotes dont l'interprétation géométrique est évidente).

6.c. Les tangentes à la parabole d'équation y = a x² à partir du point F(0,t) {a et t de signes contraires} sont en contact avec la parabole aux points T et T’ de milieu F’. F et F’ sont symétriques par rapport à O (cf : 5. Approche géométrique d'une tangente à la parabole, attention aux divergences de notation).

Télécharger la figure GéoPlan toit_cer.g2w

6.d. Toit sur une voûte parabolique

Un toit, dont les pans sont symétriques par rapport à la verticale issue du faîte du toit est soutenu par une voûte parabolique (voir la figure ci-dessous). La distance AA’ et la hauteur OH sont fixée (par exemple AA’ = 4 et OH = 2).

Déterminer la hauteur du faîte OT ainsi que le surplomb OX et la longueur des poutres pour que l'angle formé par les deux pans du toit soit droit.

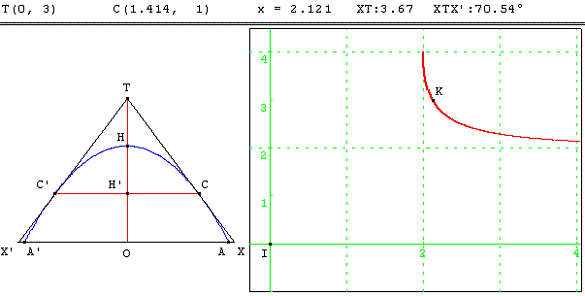
L'équation de la parabole est de la forme y = a x² + h. L'ordonnée h de H étant égale à 2 et en écrivant que les coordonnées de A vérifient cette équation on obtient :

y = 2 − .

Soit T(0, t) et H’(0, t’). On a, d'après le chapitre 5 précédent (attention aux divergences de notation), (t + t’)/2 = 2 soit t’ = 4 − t.

Pour un faîte à angle droit en calculant les coordonnées de C, on trouve t = 2,5.

Télécharger la figure GéoPlan toit_par.g2w

7. Quadrature de la parabole par la méthode d’Archimède

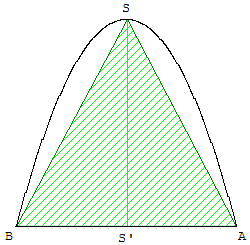
La quadrature de la parabole est le calcul de l'aire d'un segment de parabole, délimité par un arc de parabole et la corde qui le sous-tend.
C'est un des premiers calculs de surface, réalisé par Archimède (287-212 avant J.-C.).

Proposition I du livre de la méthode d'Archimède : L'aire du segment de parabole ASB est de l'aire du triangle ASB.

L'objectif est de calculer l'aire de l'arche sous la parabole, limitée par la courbe et la corde [AB] en utilisant la méthode des triangulations successives.

Voici une présentation du travail d'Archimède pour la parabole représentant la fonction f définie par f(x) = −x² + 4 (équation loin des préoccupations de l'époque où l'on parlait de section de cône rectangle).

Pentagone inscrit dans la parabole

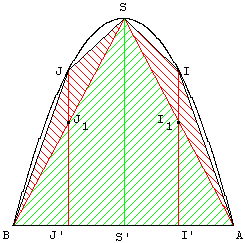
Les deux figures sont des cas particuliers (base du triangle perpendiculaire à l'axe de la parabole). Le calcul valable pour le cas général.
Avec GéoPlan, on pourra modifier la parabole ou le segment [AB].

Démonstration de la quadrature de la parabole

Le principe de la démonstration d'Archimède est :

  • de remplir l'espace entre le triangle ASB et le segment de parabole ASB par des triangles obtenus par dichotomie,
  • de parvenir, par des considérations géométriques simples à l'évaluation de l'aire de ces triangles,
  • d'établir la conjecture : « l'aire sous l'arche de parabole est de l'aire du triangle ASB »,
  • de démonstration cette conjecture par un double raisonnement par l'absurde (dépassant le cadre de la 1^ère L).

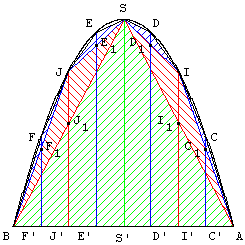
Trois étapes :

Dans la figure de gauche, qui correspond à la première étape, S’ est le milieu de [AB] et (SS’), parallèle à l'axe de la parabole, est le diamètre conjugué de AB.
L'aire du triangle ASB est égale à Ã = b × h = × SS’ × h = × 4 × 4 = 8

La deuxième étape, figure du milieu, consiste à introduire deux nouveaux triangles, ayant pour côtés respectifs [AS] et [BS] et dont les sommets I et J sont sur les parallèles à l'axe de la parabole passant par les milieux I’ de [S’A] et J’ de [S’B]. On notera I₁ et J₁ les milieux de [SA] et [SB].
L'aire du triangle ASI = × II₁ × et celle de BSJ = × JJ₁ × .
Or II₁ = JJ₁ = , l'aire cumulée des triangles est égale à × II₁ × h = × × h = Ã
L'aire des trois triangles est Ã(1 + ) = 10.

On poursuit le remplissage de la parabole, en construisant quatre nouveaux triangles, inscrits dans la parabole, de côtés [AI], [IS], [SJ], [JB] et dont les sommets sont sur les parallèles à (SS’) passant par les milieux I’ et J’, situés sur le côté.
La longueur des segments CC₁, DD₁, EE₁, FF₁ est égale à . L'aire des triangles est × CC₁ × = × × .
En cumulant ces quatre aires : × × h = Ã.
La somme des aires de ces sept triangles est : Ã(1 + + ) = 10,5.

Idées de démonstration

Archimède a démontré ces résultats par des considérations géométriques liées à la tangente en A à la parabole. On peut aussi étudier la tangente en S, parallèle à (AB).
La preuve moderne en géométrie analytique, pour une parabole d'équation f(x) = a x² + b x + c résulte des calculs (avec a < 0, pour a > 0 prendre les valeurs absolues) de :
SS’ = = − a m²,
II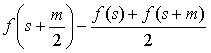₁ = = − a m² = JJ₁ = ,
DD₁ = 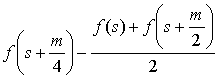= − a m² = CC₁ = EE₁ = FF₁ = .

Conclusion

Il est difficile de faire une figure pour les étapes suivantes ; à chaque étape, on rajoute ainsi des triangles dont l'aire totale est le quart de l'aire totale des triangles rajoutés à l'étape précédente.

On obtient une somme d'aires de triangles égale à la somme des termes d'une suite géométrique de raison :
Ã(1 + + + …) = Ã = Ã × = 8 × = .

Quadrature d'un arc de parabole

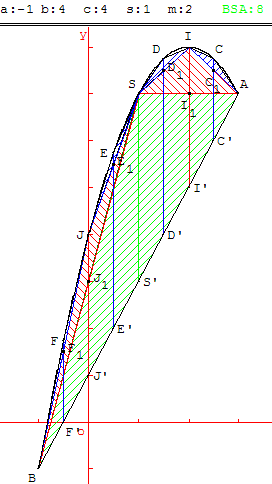
P est une parabole d'équation y = a x² + b x + c.
Pour un paramètre m l'étude se fait sur l'intervalle [s−m, s+m].
A et B sont les points de la parabole P d'abscisse s+m et s−m.
S’ est le milieu de [AB], S est sur la parabole : points d'abscisse s.

Commandes :
touche 1 : visualiser l'aire du triangle ASB et d'afficher sa valeur,
touche 2 : afficher les points I, I’, I₁, J, J’ et J₁ ainsi que les segments correspondants,
touche 3 : visualiser les aires des triangles SAI et SBJ,
touche 4 : afficher les points C, D, E, F ainsi que les segments correspondants,
touche 5 : visualiser les aires des triangles BFJ, JES, SDI et ICA.

Touches A, B, C : piloter au clavier les coefficients du trinôme, touche S, M : modifier le centre et les bornes de l'intervalle d'étude,
touche D : centrer l'intervalle d'étude au sommet de la parabole.

Mode d'emploi :
charger sur la figure avec GéoPlan,
revenir à la position initiale en tapant sur les touches 5, puis 4, 3, 2 et 1 pour retrouver le segment de parabole BSA.
Modifier éventuellement les paramètres,
construire la figure en tapant 1 pour la première étape,
puis 2, 3 pour la deuxième étape,
4 et 5 pour la troisième étape.

Télécharger la figure GéoPlan qua_para.g2w

8. Le crible géométrique de Matiiassevitch

Produit de deux naturels

Le produit de deux naturels notés sur chaque branche de la parabole, se lit directement à l'intersection du segment et de l'axe de la parabole.

En effet, considérons les points M (m, m2) et N(- n, n2) situé sur la parabole.

La droite (MN) a pour coefficient directeur : a = (m2 - n2) / (m - (-n)) = (m + n)(m - n) / (m + n) = (m - n).

La droite passe par M donc : y - m2 = (m - n) (x - m) = (m - n) x - m2 + mn.

L'équation de (MN) est y = (m - n) x + mn.

Quand x = 0 on a y = mn : la droite (MN) coupe bien l'axe (Oy) au point d'ordonnée mn.

Télécharger la figure GéoPlan mul_mati.g2w,   la figure GéoPlan pa_matia.g2w

Crible de Matiiassevitch

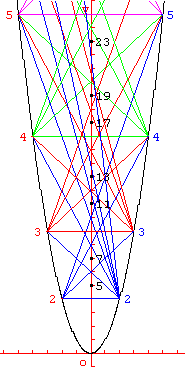
Ainsi, nous obtenons un crible géométrique très simple pour trouver les nombres premiers. Cette idée simple et géniale nous vient des mathématiciens russes Yuri Matiiassevitch et Boris Stechkin. Sur la parabole d'équation y = x2, on considère les points M et N d'abscisses respectives m et - n (m >é1, n >é1).

Le segment [MN] coupe l'axe (Oy) à l'ordonnée mn. Ainsi, en traçant tous les segments [MN] « possibles », pour m et n donnés, on peut lire sur l'axe des ordonnées tous les nombres premiers inférieurs à mn : ce sont les nombres entiers qui ne sont traversés par aucun segment [MN].

Table des matières

Problèmes de construction en 1^ère L

Inscrire, circonscrire un triangle équilatéral à un triangle donné

Inscrire un triangle équilatéral inscrit dans un carré

Inscrire un carré dans un demi-cercle

Construction d'une droite passant par un point et l'intersection de deux droites sans utiliser cette intersection inaccessible

Plus court chemin

Pavage

Dans d'autres pages du site

La Parabole en 1S

Polygones réguliers

Nombre d'or

Mobile friendly

Copyright 2003 - © Patrice Debart