Descartes et les Mathématiques
Fonctions distance
De nombreuses situations menant à des problèmes d'optimisation :
à partir de figures géométriques, études de longueurs et recherche d'extremums.
Sommaire
1. Plus court chemin
a. Symétrie axiale : de A à B via M situé sur (d)
Exercices de-ci, de-là : 486-1 construction sous contrainte
b. Translation : de A à B via M et M’
2. Trajet en temps minimum
3. Fonction distance dans un triangle
4. Fonction distance dans un hexagone
Le titre de cette page est à comprendre comme fonction faisant appel à des distances et non au sens mathématique de « fonction distance » entre les points d'un ensemble.
Technique GéoPlan : dans ces exercices est utilisée une seule figure avec deux cadres : le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction.
1. Plus court chemin
Classes de seconde, de première L
Le chemin le plus court, problème ouvert maths
Constructions avec une contrainte d'optimisation
(et ici utilisation d'une transformation)
Proverbe malien : le plus court chemin d'un point à un autre est le rêve.
1.a. Symétrie axiale : de A à B via M situé sur (d)
Mathématique - Problème ouvert :
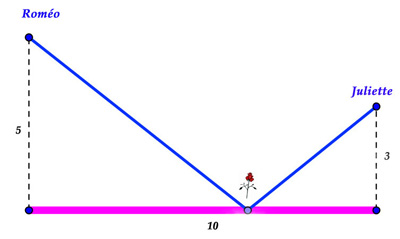
Roméo doit aller cueillir une fleur sur le mur de roses et la porter à Juliette. À quel endroit Roméo doit-il cueillir la fleur pour aller le plus vite possible ?
Prérequis : configurations du plan, théorèmes de Pythagore et de Thalès, transformations, calculs avec fractions et racines carrées, généralités sur les fonctions.
Déroulement de l'activité :
Le problème est à chercher à la maison, puis, en salle informatique et en demi-groupe, on demande aux élèves de réaliser une figure avec un logiciel de géométrie dynamique pour confirmer ou affiner les résultats trouvés à la maison.
De retour en classe entière, pour la correction, le professeur projette la figure dynamique tout en déroulant les calculs.
Prolongement : la vitesse pour aller au mur de roses n'est pas la même que la vitesse pour aller rejoindre Juliette. Non résolu.
Étude fonctionnelle avec GéoPlan
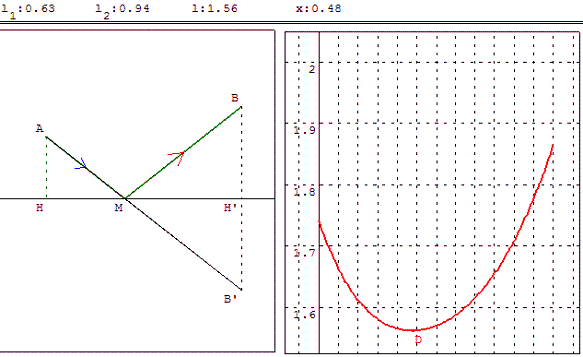
Étant donné deux points A et B situés dans un même demi-plan par rapport à une droite (d), trouver le point M sur la droite (d) tel que MA + MB soit minimum.
On trouve la solution en trouvant l'intersection M de la droite (d) avec la droite (AB’) où B’ est le symétrique de B par rapport à (d).
M est aussi le point de (d) tel que la perpendiculaire en M à (d) soit la bissectrice des droites (MA) et (MB).
Ainsi, le point A représente la position initiale d'une boule de billard qui rebondit en M pour terminer en B.
Technique GéoPlan
Dans chacun de mes exemples, déplacer le point variable de la fenêtre de gauche avec la souris ou les flèches du clavier.
La touche T permet le Tracé point par point du graphe de la fonction,
touche S pour Sortir du mode trace,
touche L pour le dessin en bloc de la représentation graphique.
Télécharger la figure GéoPlan symet.g2w
1.b. Sans sortir du cadre
Construction sans traverser la rivière
Exercices de-ci, de-là : 486−1
Étant donné deux points A et B situés dans un même demi-plan par rapport à une droite (d), trouver le point M sur la droite (d) qui minimise MA + MB, sans sortir du cadre.
Solution se ramenant à la symétrie
« On peut raisonner sans contrainte… » !
Georges Lion
Il s'agit de se ramener à la solution connue qui utilise le symétrique A’ de A par rapport à (d).
On peut trouver la construction de M, à l'aide d'un point C sans avoir placé A’ :
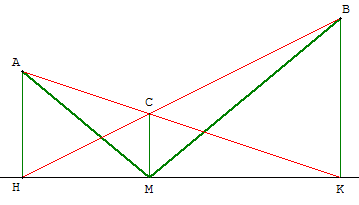
(AK) et (BH) se coupent C.
La projection M de C sur (d) est alors la solution.
Télécharger la figure GéoPlan symet_contrainte.g2w
Démonstration
À priori, il semble qu'on n'échappe pas à l'utilisation du symétrique A’ pour la démonstration, comme le propose Jean Fromentin :
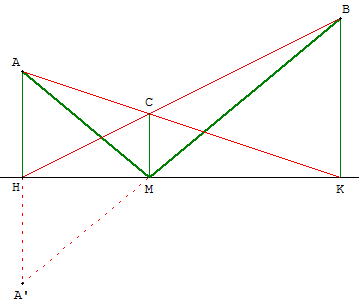
A’ symétrique de A par rapport à (d) ; (AA’) // (BK),
(AK) et (HB) se coupent en C.
(BA’) coupe (d) en M.
D'après le théorème de Thalès 
(= 
) = 
.
De même (
=) 
= 
.
Or HA = HA’
Donc = .
De ce fait, (MC) // (AH) // (BK).
Cette condition nécessaire est aussi suffisante. Ainsi pour trouver le point M il suffit de construire le point C et d'en abaisser la perpendiculaire sur (d).
Voir autres solutions et activités dans le bulletin APMEP no 488.
Trouver le calcul de CM dans le problème de la barrière.
1.c. Translation : de A à B via M et M’
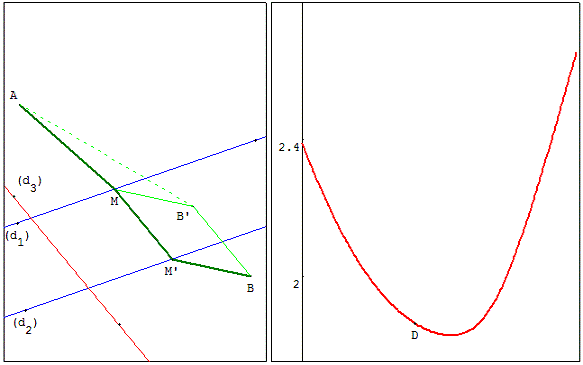
Soit deux droites parallèles (d1) et (d2), deux points A et B de part et d'autre de la bande dessinée par (d1) et (d2)
et (d3) une droite sécante à (d1) et d2).
Construire les points M et M’ sur (d1) et (d2) tels que (MM’) soit parallèle à (d3) et le trajet AM + MM’ + MB soit le plus court possible.
Télécharger la figure GéoPlan dist_min_trans.g2w
2. Modélisation d'une situation géométrique
En géométrie plane, recherche d'un trajet optimal avec deux contraintes différentes suivant les régions du plan dans lesquelles on se déplace.
ÉduSCOL −Terminale S − Banque de sujets 2005 − 2007 : sujet 016
Trajet en temps minimum
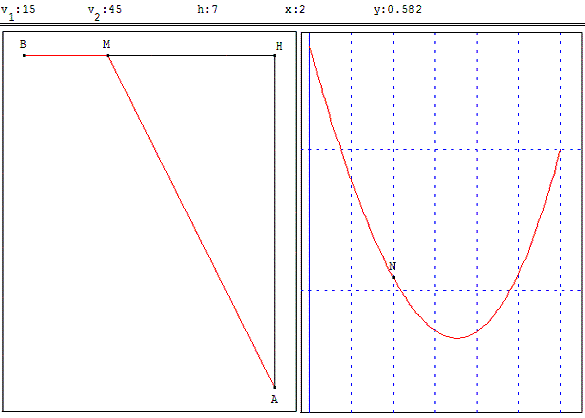
Un marin désire aller de son phare A à la ville B située sur une côte rectiligne BH.
Il transporte dans son bateau son vélo.
En mer il se déplace à la vitesse v1, sur terre à la vitesse v2 (v1 ≤ v2).
En quel point M de la côte doit-il aborder, pour mettre le moins de temps possible ?
La distance BH est égale à 6 km, la distance AH vaut h.
On appelle x la distance BM, y le temps mis pour aller de A à B (en passant par M) en fonction de x.
Le point N de coordonnées (x, y) varie dans un repère orthogonal R.
Télécharger la figure GéoPlan min_temps.g2w
Variante sans bateau : analyse en 1L
Thème « optimisation »
CAPES Externe de mathématiques 2011
L'exercice
À partir de l'extrait d'un manuel donné ci-dessous, un professeur a proposé à ses élèves l'exercice suivant :
Soit f la fonction définie sur l'intervalle [0 ; 4] par :
f(x) = 
1. Expliquez pourquoi la fonction f est dérivable et calculer sa dérivée.
2. Dressez le tableau de variation de f. Déterminer pour quelle valeur x0cette fonction admet un minimum.
3. Donnez les valeurs exactes, puis les valeurs approchées arrondies à 10−3 de x0 et de f(x0).
Un extrait de manuel
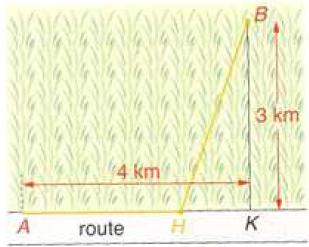
Une voiture 4 × 4 doit aller d'un point A situé sur une route à un point B en traversant un champ.
Sachant que sa vitesse sur la route est de 40 km·h− 1 et que sa vitesse â travers champs est de 20 km·h− 1, déterminer la position du point H pour que le temps mis pour aller de A à B soit minimal.
Déclic Terminale S − 2006
Le travail à exposer devant le jury
1 – Comparez les compétences développées par les deux versions de l'exercice (professeur/manuel).
2 – Citez différents logiciels permettant d'émettre une conjecture sur la solution de l'exercice du manuel et développez la mise en oeuvre de l'un d'entre eux.
3 – Proposez la correction de la question 2) de l'exercice du professeur comme vous la présenteriez à des élèves.
4 – Présentez deux ou trois exercices sur le thème « optimisation ».
3. Fonction distance dans un triangle
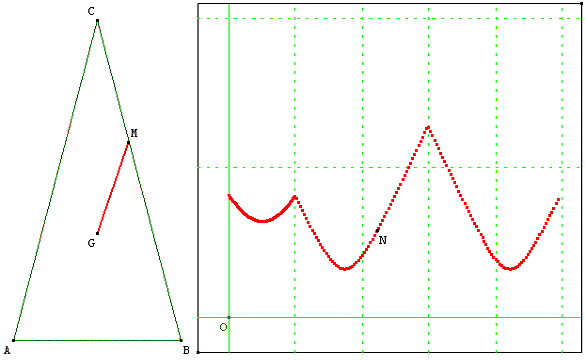
Au démarrage G est le centre de gravité d'un triangle ABC.
Un point M varie sur les côtés du triangle ABC. Le point M part de A et parcourt le triangle ABC dans le sens trigonométrique.
On appelle x la distance parcourue depuis A (unité AB = 1). On étudie les variations de la longueur du segment [MG] en fonction de x.
Le point N a pour coordonnées (x, MG) dans un repère orthogonal R dont les unités sont u et v.
Télécharger la figure GéoPlan fct_triangle.g2w
4. Fonction distance dans un hexagone
Énoncé (Terminale S)
ABCDEF est un hexagone régulier de côté de longueur 2.
Un point M part de A et fait le tour de l'hexagone dans le sens positif.
On note xN la distance que M a parcourue depuis son départ sur l'hexagone. On note yN = AM la distance (directe) de A à M.
Dans le repère situé à droite, on place le point N de coordonnées (xN ; yN) et on trace le lieu L de N quand xN varie de 0 à 12.
On obtient ainsi une fonction définie sur [0 ; 12] par morceaux à valeurs dans [0 ; 4].
Résolution du problème
On essaiera d'exprimer la distance AM selon les trois cas de segment après avoir remarqué la symétrie.
La composition des fonctions sera utile pour une étude rigoureuse.
Le tableau de variation complet doit être établi.
Utilisation du logiciel
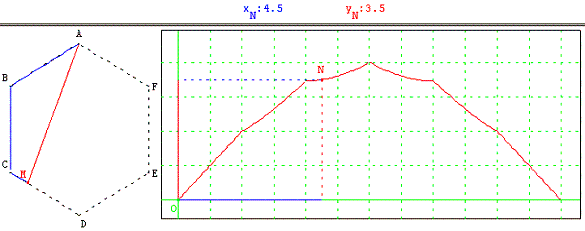
L'intérêt est de suivre les positions correspondantes simultanément et de montrer que la même variation de x donne des différences selon la position de M.
Télécharger la figure GéoPlan fct_hexagone.g2w
Table des matières
Dans d'autres pages du site
Menu optimisation
Longueur minimum en 3e
Seconde : Problèmes d'optimisation
1S - TS : Problèmes d'optimisation
Études d'aires : minimum-maximum
Maximum faisant intervenir une parabole : Analyse en 1L avec GéoPlan
Google friendly
|
|
Page no 41, créée le 28/5/2003 |