Descartes et les Mathématiques pour mobiles

Le théorème de Thalès

Les mathématiques en quatrième et troisième :
démonstration de Thalès par Euclide et dix exercices.

Sommaire

1. Démonstration par Euclide avec la méthode des aires

2. Thalès et médiane

3. Concours au centre de gravité

4. Quadrilatère et droites parallèles

5. Parallèle à une diagonale d'un quadrilatère

6. Moyennes géométriques

7. Barrière - Deux échelles

8. Constructions des inverses des premiers naturels

II. Réciproque du théorème de Thalès
1. Cordes parallèles

2. Petit théorème de Pappus

3. Quadrilatère et parallèles

Les théorèmes de Thalès

Thalès a vécu à Milet au VI^e siècle avant J.-C.

Mathématicien et philosophe
grec de l'école ionienne,
l'un des sept sages de la Grèce,
il fut le premier à donner une
explication rationnelle,
et non mythologique,
de l'univers, en faisant
de l'eau l'élément premier.

Il connaissait l'égalité
des angles du triangle
isocèle et des angles opposés par le sommet ainsi
que la somme des angles d'un triangle.

On attribue le premier raisonnement géométrique à Thalès :
pour mesurer la hauteur d'une pyramide, il eut l'idée de
mesurer la longueur de l'ombre de la pyramide sur le
sol et la longueur de l'ombre d'un bâton. Il montrera que
le rapport de la pyramide avec son ombre était le rapport
que le bâton avec la sienne.

Deux grands théorèmes de géométrie lui sont attribués :

  – Notre théorème de géométrie affine étudié dans
les classes de la quatrième à la seconde.
Nous pouvons distinguer trois versions de ce théorème :

• le grand théorème direct de Thalès :
  des droites parallèles déterminent sur deux sécantes
  des segments homologues proportionnels ;
• le théorème de Thalès appliqué au triangle :
  pour un triangle ABC, si M est un point de (AB),
  N un point de (AC) et si (MN) est parallèle à (BC),
  alors = = ,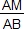
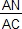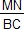  deux triangles en configuration de Thalès sont
  semblables, ou de même forme,
  une homothétie de centre A transforme le triangle ABC en AMN ;
• sa réciproque :
  dans un triangle ABC, si les points A, B et M sont alignés,
  si les points A, C et N sont alignés dans le même ordre
  que A, B et M et si, de plus, les rapports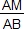 et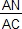
  sont égaux alors les droites (MN) et (BC) sont parallèles.

    – On attribue plus sûrement à Thalès
       l'inscription du triangle rectangle
       dans un demi-cercle, plus connue comme théorème de
       Thalès outre-Manche ou outre-Rhin que chez nous :

Un angle inscrit dans un demi-cercle est droit.

À cette occasion, d'après la légende, il sacrifia un bœuf.

en : Thales’ theorem :
       an inscribed angle in a semi-circle is a right angle.

de : Satz des Thales :
       der winker in Halbkreis ist ein rechter.

Extrait du programme de géométrie de 4^e (2007)

Contenu

Triangles déterminés par deux droites
parallèles coupant deux sécantes.

Compétences exigibles

Connaître et utiliser
la proportionnalité
des longueurs pour les
côtés des deux triangles
déterminés par deux droites parallèles coupant deux sécantes :

Dans un triangle ABC, si M est un point du côté [AB],
N un point du côté [AC] et si [MN] est parallèle à (BC), alors

= = .

Figure interactive dans GeoGebraTube : Thalès dans un triangle

Commentaires

L'égalité des trois rapports est admise après avoir
été étudiée dans des cas particuliers de rapport.
Elle s'étend au cas où M et N sont respectivement
sur les demi-droites [AB) et [AC).

Le cas où les points M et B sont de part et d'autre
de A n'est pas étudié (configuration du papillon).
Le théorème de Thalès dans toute sa généralité
et sa réciproque seront étudiés en classe de troisième.

Accompagnement des programmes de 4^e (1998)

En classe de 4^e, on demande de façon plus systématique
de repérer et de mettre en œuvre les théorèmes appropriés.
Le recours, si besoin est, à plusieurs pas de démonstration
amène à comprendre le changement de statut d'une
assertion au fil d'une démonstration :
un résultat intermédiaire est une conclusion dans un pas
de démonstration et une hypothèse dans un pas ultérieur.

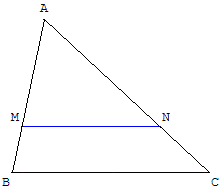
Par exemple, à propos des
« triangles déterminés par
deux droites parallèles
coupant deux sécantes »,
l'étude d'un cas particulier
de « l'égalité des rapports »
(valeur ) repose sur une
telle démarche.

On a coupé un des côtés
d'un triangle ABC en trois
segments de même longueur :
AI = IK = KB.

Par I et K, on a mené
les parallèles au côté [BC], qui coupent [AC] en J et L respectivement.

À l'aide des résultats sur les milieux de deux côtés d'un triangle,
on souhaite établir que le côté [AC] se trouve lui aussi coupé
en trois régulièrement : AJ = JL = LC.

On pourra remarquer que contrairement aux deux cas évoqués
pour la classe de 5^e, l'évidence « visuelle » du résultat ne fait
ici guère de doute ; la question qui se pose est donc celle de
l'établir au moyen des résultats déjà acquis.

La première des deux égalités ci-dessus est simple à établir,
dès que l'on a remarqué que I est le milieu de [AK].
Le second (dans l'ordre des programmes) théorème des milieux
appliqué au triangle AKL permet alors de conclure.
La seconde égalité est autrement plus difficile et il se peut très
bien que dans une classe, l'idée du tracé d'un segment auxiliaire
convenable, par exemple celui du segment [BJ], ne surgisse
pas d'elle-même et doive être indiquée par le professeur.

La mise en forme de la démonstration a tout son intérêt dans un cas
comme dans l'autre. Notons M le point d'intersection des droites
(BJ) et (KL). Le second (dans l'ordre des programmes)
théorème des milieux appliqué au triangle BIJ permet de
conclure que le point M est le milieu de [BJ]. Ce résultat
acquis devient alors une hypothèse, qui permet à nouveau
l'application du second théorème des milieux, cette fois
au triangle JBC, pour conclure que L est le milieu de [IC].

Ainsi, deux pas de démonstration enchaînés ont conduit
à la conclusion : JL = LC.

Si l'on considère la même figure, mais maintenant avec
les hypothèses que les côtés du triangle sont coupés
en trois segments de même longueur :
AI = IK = KB et AJ = JL = LC, la démonstration du
parallélisme des droites (IJ), (KL) et (BC) repose
sur la même idée de tracé d'un segment auxiliaire.

Mais on s'aperçoit que la démonstration suppose
ici l'utilisation des deux théorèmes des milieux.
La différence des compétences mises en jeu par
la recherche d'une démonstration et par sa rédaction
se trouve ainsi bien mise en évidence.

1. Euclide : démonstration par la méthode des aires

Les Éléments d'Euclide - livre VI - Proposition 2

Méthode des aires : démonstration du théorème
de Thalès utilisant la propriété d'Euclide :
« les triangles qui ont la même hauteur sont l'un
relativement à l'autre comme leurs bases ».

1.a. Thalès a découvert le théorème, mais c'est Euclide qui l'a prouvé.

Démonstration d'Euclide

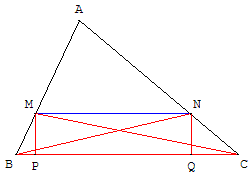
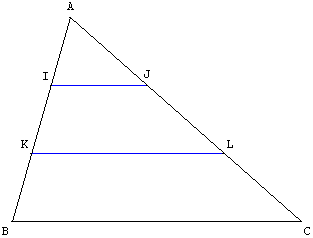
Les triangles MBC et NBC
ont le côté [BC] commun ;
les troisièmes sommets
sont sur une parallèle
à ce côté commun ;

ils ont des hauteurs
MP et NQ égales ;
ces deux triangles
ont la même aire et
par complément
dans le triangle ABC
on a l'égalité des aires :
A(AMC) = A(ABN).

En divisant les deux termes de cette égalité par A(ABC) on a :

= .

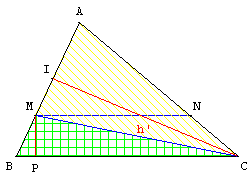
Soit h’ = CI la hauteur en C
des triangles AMC et ABC.

On a :
A(AMC) = AM ×
et A(ABC) = AB × .

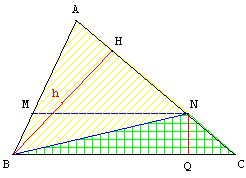
Enfin h = BH la hauteur en B
des triangles ABN et ABC.
On a : A(ABN) = AN ×
et A(ABC) = AC × .

Les rapports des aires sont
= =
et = = .

Conclusion : = .

1.b. Calcul de

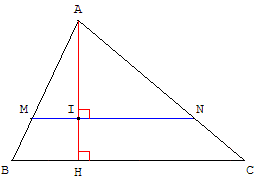
Soit [AH] la hauteur en A
du triangle ABC qui coupe
(MN) en I.

Dans les triangles rectangles
ABH et AHC la propriété de
Thalès permet d'écrire
= = .

Les triangles INH et INC ont la même aire,
car le côté [IN] est commun et les troisièmes
sommets sont sur une parallèle à ce côté commun.
En ajoutant l'aire du triangle AIN on a : A(AHN) = A(AIC).

Or A(AHN) = × AH × IN
et A(AIC) = × AI × HC soit AH × IN = AI × HC d'où = .

On démontre, de même, que = .

Un calcul sur les proportions = = = = =
permet de conclure que : = = .

1.c. Autre démonstration par les aires

On étudie l'égalité des aires des triangles MNB et
MNC et on calcule de deux façons l'aire de AMN.
On en déduit une première égalité du grand théorème de Thalès :
« Toute parallèle à l'un des côtés d'un triangle
divise les deux autres côtés en segments proportionnels ».
On transforme cette égalité pour obtenir
le Théorème de Thalès dans le triangle.

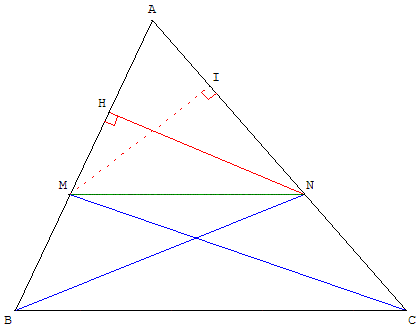
(MN) est parallèle à (BC).

Les triangles MNB et MNC ont même base [MN] et leurs
hauteurs sont égales à la distance entre les deux parallèles.
Leurs aires A(MNB) et A(MNC) sont égales (propriété du trapèze).

Les triangles AMN et MNB ont pour hauteur commune [NH],
où H est la projection de N sur le support des bases (AB). Leurs aires sont :
A(AMN) = AM × NH et A(MNB) = MB × NH.
Le rapport de ces deux aires est = .

Les triangles AMN et MNC ont pour hauteur commune [MI]. a
Le rapport de leurs aires est = .

Ces deux rapports d'aires, avec un numérateur égal
à A(AMN) et des dénominateurs A(MNB) et
A(MNC) égaux, sont des rapports égaux :

= , donc = .

En permutant les « moyens » = .

Ce calcul a donc permis d'obtenir
le grand théorème de Thalès :
les droites parallèles (BC), (MN),
et une troisième parallèle passant par A,
déterminent sur les sécantes (AB) et (AC)
des segments homologues proportionnels.

De là, le calcul sur les proportions :
= = = , permet, en permutant les
« moyens » entre le premier et le dernier rapport,
de démontrer la formule de Thalès appliquée au triangle : = .

2. Thalès et médiane

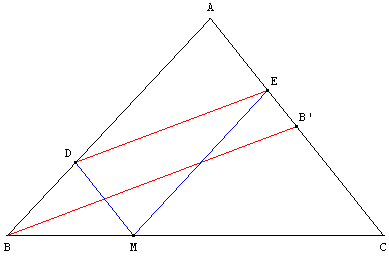
ABC est un triangle, [BB’] est une médiane.

M est le point du segment [BC] tel que BM = BC.
Les parallèles menées par M à (AC) et à (AB)
coupent respectivement (AB) et (AC) en D et en E.

En utilisant deux fois le théorème de Thalès,
calculer les rapports et .

Montrer, avec la réciproque de Thalès,
que les droites (DE) et (BB’) sont parallèles.

3. Concours au centre de gravité

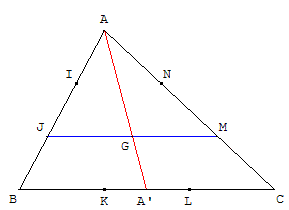
Chacun des côtés
d'un triangle ABC
est partagé en trois
segments de même longueur ;
grâce aux points :
I et J sur [AB],
K et L sur [BC],
M et N sur [CA].

1. Montrer que le
centre de gravité
du triangle ABC
est le milieu de [JM].
2. En déduire que les droites (IL), (JM) et (KN) sont concourantes en G.

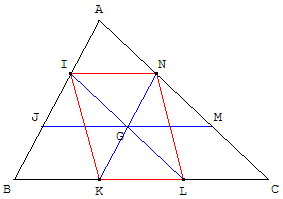
Remarque : Il est aussi possible
de montrer que KLNI
est un parallélogramme.

Voir l'utilisation de barycentres

4. Quadrilatère et droites parallèles

Milieux de deux côtés

Un quadrilatère quelconque ABCD,
I et J sont les milieux de deux
côtés [AB] et [BC].

Par I et J nous menons des
parallèles aux côtés (AD) et (CD).
K intersection des deux parallèles
est aussi le milieu de [BD].

Les parallèles menées par I et J
coupent [BD] en son milieu K.

Ceci se démontre en utilisant
deux fois le théorème des milieux.

Partage proportionnel de deux côtés

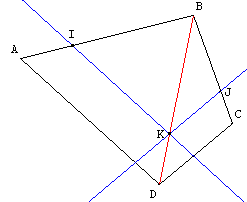
Nous pouvons refaire une autre
figure généralisant le problème :
Si les points I et J partagent [BA]
et [BC] dans le même rapport,
les parallèles se coupent
sur (BD) et K partage
[BD] pareillement.

Ceci se démontre en utilisant
deux fois Thalès.

Remarque : par la réciproque
de Thalès on montre comme
dans l'exercice suivant que
(IJ) est parallèle à (AC).

5. Parallèle à une diagonale d'un quadrilatère

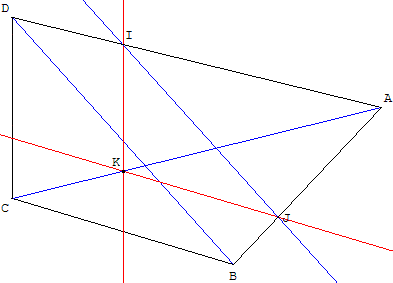
ABCD est un quadrilatère quelconque,
I un point sur le côté [DA].
Nous construisons la parallèle à (CD) menée par I.
Cette parallèle coupe la diagonale [AC] en K.

Par K nous menons la parallèle à (BC) qui recoupe [AB] en J.

Montrer que les droites (IJ) et (BD) sont parallèles.

Indication : en utilisant deux fois la propriété de Thalès
nous pouvons montrer l'égalité des rapports et ,
puis démontrer que (IJ) et (BD) sont parallèles avec
la réciproque de Thalès.

Variante : I est le milieu du côté [DA].
Montrer que le point K est le milieu de [AC],
que J est le milieu de [AB] et en déduire
que (IJ) et (BD) sont parallèles.

6. Moyennes géométriques

Dans un triangle

Classe de 3^e

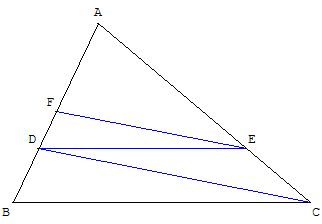
Dans un triangle ABC, D
est un point du segment [AB].
Placer le point E tel que :
(DE) // (BC) et (EF) // (CD).

En utilisant ces deux
hypothèses l'une après l'autre,
en écrivant les rapports de
Thalès égaux, démontrer
que l'on a :

AD² = AF × AB.

Dans un angle

Classe de 2^nde

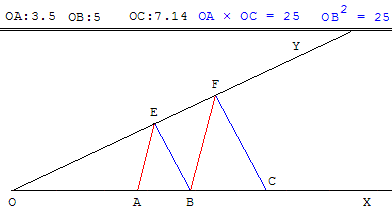
Soit A et B deux points sur une demi-droite [OX) et E un point sur [OY).

Placer les points F sur [OY) et C sur [OX) tels que
les droites (AE) et (BF) soient parallèles, ainsi que les droites (BE) et (CF).

En écrivant des rapports de Thalès égaux, montrer que OB² = OA × OC.

7. Barrière

Un chemin bordé par deux murs [AA’] et [BB’],
de hauteurs a et b est barré par deux chevrons en bois [AB’] et [BA’].

De quoi peut bien dépendre la hauteur h laissée libre ?

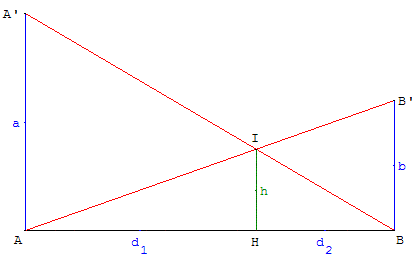
Déplacements

Déplacer A’ ou B’ montre que h dépend certainement de a et b.

Déplacer A ou B pour montrer que contrairement à ce
que l'on pourrait penser, cette hauteur h ne dépend
pas de la distance AB.

Démonstration

Les droites (A’A) et (IH) perpendiculaires à (AB) sont parallèles.
La propriété de Thalès dans le triangle BAA’ permet d'écrire = .
Et = d'après la propriété de Thalès dans le triangle ABB’.
D'où il vient + = = 1 ou encore h( + ) = 1
soit = + et h = .

A’H + HB’ est la plus courte distance de A’ à B’
en passant par la droite (AB)

7.b. Deux échelles

Une échelle AB’ de 2 mètres et une échelle BA’ de
3 mètres se croisent à un mètre du sol dans un chemin bordé par deux murs.
Quelle est la largeur du chemin ?

Recherche

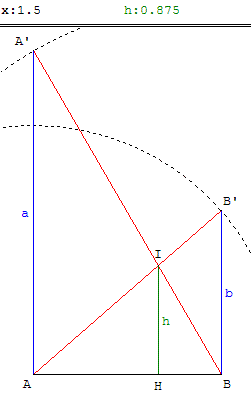
Déplacer le point B jusqu'à
ce que h soit égal à 1.
On trouve un chemin
de 1,23 m de large.

Solution (TS)

On a montré dans l'exercice
ci-dessus que + = .

Si x est la largeur du
chemin (0 < x < 2),
d'après le théorème
de Pythagore,
dans le triangle AA’B
rectangle en A : 9 - x² = a²
et dans le triangle BB’A
rectangle en B : 4 - x² = b².

Pour h = 1, la relation + = 1
donne l'équation .

Une méthode numérique permet
de résoudre cette équation.
La calculatrice TI-92 permet
de trouver deux solutions opposées.
La solution positive x ≈ 1,23 convient.

8. Constructions des inverses des naturels

Premiers inverses

Classe de seconde

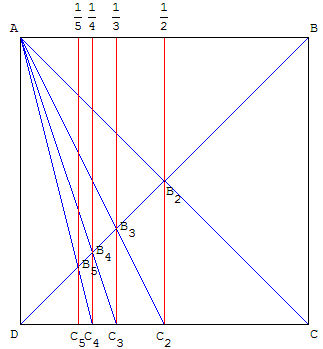
Dans un carré ABCD
de côté 1, le point C₁
placé en C a pour
abscisse 1 dans le
repère (D, C) de
la droite (DC).
La droite (AC₁)
et la diagonale (BD)
se coupent en B₂
milieu du carré,
qui se projette sur
(DC) en C₂ d'abscisse .
La droite (AC₂) et
la diagonale (BD)
se coupent en B₃ qui
se projette en C₃
d'abscisse .
Et ainsi de suite…

Cas général : inverse de n

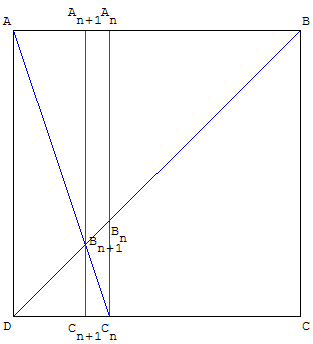
En répétant n fois ce
processus,
on obtient les points
B_n et C_n tels que
DC_n = C_nB_n = .
La droite (AC_n) et
la diagonale (BD)
se coupent en B_n+1
qui se projette sur
(DC) en C_n+1.

En reprenant les
notations de
l'exercice 7, on a :
DA = a = 1,
C_nB_n = b =
et h = C_n+1B_n+1

On a donc = + = 1 + n et h = .
DC_n+1 = C_n+1B_n+1 = .

En classe de première on dira
que l'on a démontré par récurrence la propriété :
pour tout naturel n, C_n a pour abscisse .

II. Réciproque du théorème de Thalès

Hors programme du collège

II.1. Cordes parallèles

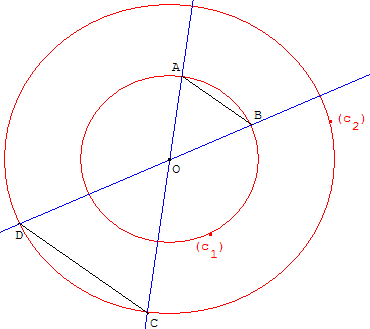
Deux cercles (c₁) et (c₂) de rayons r et r’ ont même centre O.

Deux droites (d₁) et (d₂), passant par ce centre O,
coupent le premier cercle en A et B et le deuxième
en C et D. Que peut-on dire des droites (AB) et (CD) ?
Le démontrer.

. D'après la réciproque du théorème de Thalès
(AB) et (CD) sont parallèles.

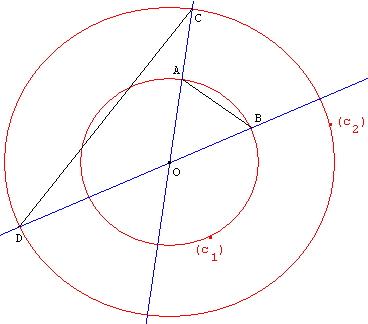
Oui, mais le contre-exemple ci-dessous montre que c'est faux.
Il faut préciser que les points O, A, C et O, B, D sont dans le même
ordre sur les deux droites (d₁) et (d₂),
ce qui n'est le cas que sur la figure ci-dessus.

Faire une figure où ce n'est pas le cas :

II.2. Petit théorème de Pappus

La figure n'a pas encore été transférée de l'ancien site Orange

Pappus d'Alexandrie (vers l'an 300)

Placer un point O,
tracer deux demi-droites (d₁) et (d₂), issues de O.

Placer les points A et B sur la première demi-droite,
D et E sur la deuxième demi-droite et tracer les
segments [AE] et [BD],
tracer la droite passant par B parallèle à la droite (AE).
Cette droite coupe la demi-droite [OD) en F.
Tracer la droite passant par E parallèle à la droite (BD).
Cette droite coupe la demi-droite [OA) en C.

Déplacer les points variables A, B, D ou E sur les
demi-droites. Que peut dire des droites (AD) et (CF) ?

Œuvres de Pappus

Théorème de Pappus : plan projectif

Parallélogramme de Pappus : preuve par homothétie

Démonstration par Pappus du théorème de Pythagore

Le problème de Pappus

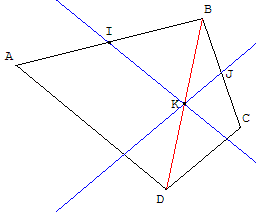
II.3. Quadrilatère et parallèles

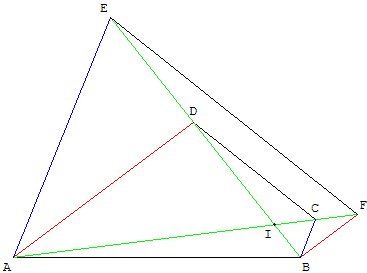
ABCD est un quadrilatère convexe.
On suppose que la parallèle à (BC), passant par A,
coupe (BD) en E et que la parallèle à (AD), passant par B, coupe (AC) en F.

Montrer que la droite (EF) est parallèle à (CD).

Indications

Soit I le point d'intersection des diagonales.

Sachant que (AE)//(BC), la propriété de Thalès
dans les triangles IAE et ICB permet d'écrire l'égalité :
= ,
De même, comme (AD)//(BF), la propriété de Thalès
dans les triangles IDA et IBF permet d'écrire :
= .

En effectuant le quotient de ces deux égalités et
après simplification de IA et IB, on trouve = .
La réciproque de Thalès permet de conclure que
(EF) est parallèle à (CD).

Table des matières

La géométrie au collège

Dans d'autres pages du site

Démonstrations géométriques de Pythagore

La Géométrie de Descartes (lycée)

Sur ordinateur, cette page pour grand écran

Mobile friendly