 Descartes et les Mathématiques
Descartes et les Mathématiques
Aire du triangle
Des images aux formules :
calcul de l'aire d'un triangle par diverses méthodes de découpage.
Sommaire
3. La propriété du trapèze
5. La propriété des proportions, théorème du chevron
6. Partage en deux d'un triangle - Olympiades 2004
7. Pliage d'un triangle selon une droite des milieux
8. Transformer un quadrilatère en triangle - Olympiades 2008
Comment calculer l'aire d un triangle ?
La formule de l'aire d'un triangle est :
Aire d'un triangle = (Base × hauteur) / 2 soit : A = (B × h) / 2.
1. Aire de la surface d'un triangle
Classe de cinquième
1.a. Transformer un triangle en rectangle
Angle en B aigu
Comment calculer l'aire d'un triangle
Doublement de l'aire du triangle
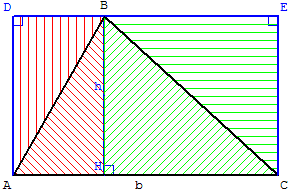
Le rectangle ACED a une aire
double de celle du triangle ABC.
2 Aire(ABC) = Aire(ACED)
= AC × BH = bh
Tangram d'Abul Wafa
Faire pivoter de deux triangles rectangles
découpés au-dessus de la droite des milieux (A’C’)
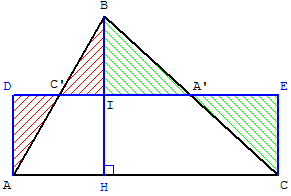
Le rectangle ACED a même aire
que celle du triangle ABC.
Aire(ABC) = Aire(ACED)
= IH × AC = ![]() hb.
hb.
![]() Animation de Christian Mercat
Animation de Christian Mercat
GeoGebraTube : Tangram d'Abul Wafa
Découpe de deux autres triangles
qui pivotent autour des milieux A’ et C’
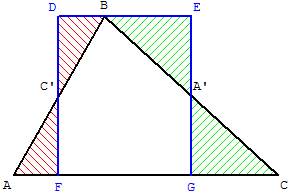
Le rectangle FGED a même
aire que celle du triangle ABC.
Aire(ABC) = Aire(FGED)
= FG × DF = ![]() bh.
bh.
Quadrature du triangle : il est possible de transformer
le triangle en carré avec la quadrature du rectangle.
Calculer l'aire d'un triangle
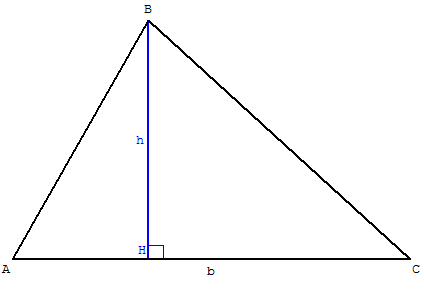
L'aire d'un triangle a pour mesure le demi-produit
d'un côté par la hauteur perpendiculaire à ce côté.
Aire(ABC) = ![]() base × hauteur.
base × hauteur.
Comme h = AB sin A = c sin A, on a aussi
Aire(ABC) = ![]() bc sin A.
bc sin A.
Au lycée, voir la formule de Héron d'Alexandrie
dans l'article : relations métriques du triangle.
1.b. Transformer un triangle avec un angle obtus
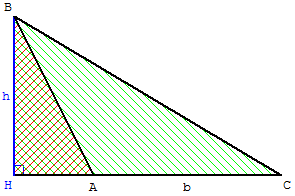
On procède par différence :
Aire(ABC)
= Aire(HBC) - Aire(HAB)
On retrouve la même formule :
Aire(ABC)
= ![]() BH × HC -
BH × HC - ![]() B × HA
B × HA
= ![]() BH × AC =
BH × AC = ![]() hb.
hb.
Doublement de l'aire du triangle
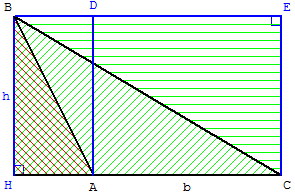
Le rectangle HCEB a une aire
double de celle du triangle HBC.
Le rectangle HADB a une aire
double de celle du triangle HAB.
On procède par différence :
Aire(ACED)
= Aire(HCEB) - Aire(HADB).
Le rectangle ACED a une
aire double de celle
du triangle ABC.
1.c. Transformer un triangle en parallélogramme
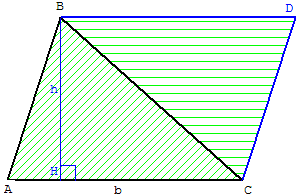
« Aire du triangle, moitié
du parallélogramme ! »
Doublement de l'aire
du triangle
Le parallélogramme ACDB
a
une aire
double de
celle du triangle ABC.
Le parallélogramme a pour base b
et pour hauteur h.
2 Aire(ABC) = Aire(ACDB) = AC × BH = bh
Faire pivoter, autour de A’, le triangle découpé
au-dessus de la droite des milieux (A’C’)
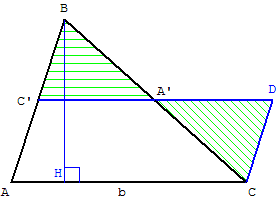
Le parallélogramme ACDC
a même aire que celle du
triangle ABC.
Le parallélogramme a pour
base b et pour hauteur ![]() h.
h.
Aire(ABC) = Aire(ACDC’)
= ![]() h × AC =
h × AC = ![]() hb
hb
Faire pivoter, autour de A’, le triangle A’B’C
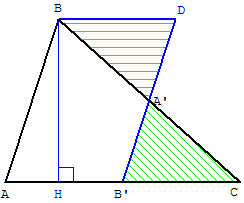
Le parallélogramme AB’DB a même
aire que celle du triangle ABC.
Le parallélogramme a pour
base ![]() b et pour hauteur h.
b et pour hauteur h.
Aire(ABC) = Aire(AB’DB)
= AB’ × BH = ![]() bh
bh
2. Aire du triangle rectangle
Pour calculer l'aire d'un triangle rectangle,
on peut utiliser la formule de l'aire d'un rectangle :
produit des petits côtés, puis diviser le résultat par 2.
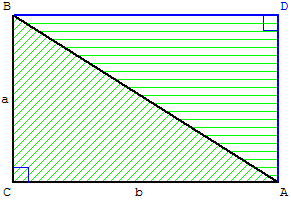
Doublement de
l'aire du triangle
Le rectangle ACBD
a une aire double
de celle du triangle
rectangle ACB.
2 Aire(ACB) = Aire(ACBD)
= CB × CA = ab.
Faire pivoter, autour de O, milieu de [AB], le triangle
découpé à droite de la droite des milieux (OB’)
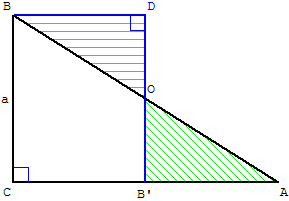
Le rectangle CBDB’ a même
aire que celle du triangle ABC.
Aire(ABC) = Aire(CBDB’)
= CB × CB’= ![]() ab
ab
Faire pivoter, autour de O, le triangle découpé
au-dessus de la droite des milieux (OA’)
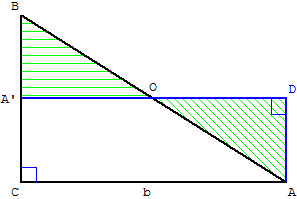
Le rectangle CA’DA a même
aire que celle du triangle ABC.
Aire(ABC) = Aire(CA’DA)
= CA’× CA = ![]() ab
ab
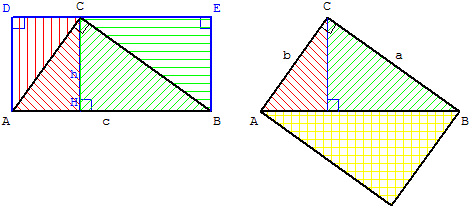
L'aire du triangle ABC, rectangle en C, se calcule de deux façons,
avec la formule ![]() base × hauteur et on a :
base × hauteur et on a :
– le calcul de l'aire du triangle rectangle avec l'hypoténuse
et de la hauteur
Aire(ABC) = ![]() AB × CH =
AB × CH = ![]() ch,
ch,
– ou le calcul de l'aire du triangle rectangle avec les côtés de l'angle
droit (cathètes) ; CA comme base, CB comme hauteur
Aire(ABC) = ![]() CA × CB =
CA × CB = ![]() ba.
ba.
D'où CA × CB = AB × CH : dans un triangle rectangle,
le produit des cathètes est égal au produit de
l'hypoténuse et de la hauteur issue du sommet de l'angle droit.
Voir : relations métriques dans le triangle rectangle au lycée
Figures clés
Le recours à des figures-clés repose sur la reconnaissance
d'un modèle déjà rencontré.
Cela suppose donc l'existence d'une base de référence constituée
de configurations et de théorèmes
associés. C'est le cas de la
plupart des théorèmes mis en place au collège (propriétés
caractéristiques des quadrilatères, propriétés des angles
obtenus en coupant deux parallèles par une sécante,
configurations de Thalès, de Pythagore, concours
de droites remarquables dans un triangle…).
Il en est d'autres qui ne sont pas l'objet de compétences décrites dans le
programme, mais qui, dans la mesure où elles reviennent souvent,
finissent par fixer des connaissances à leur propos.
Ainsi, les résultats ci-dessous, relatifs aux aires de triangles peuvent
constituer des figures-références « complémentaires ».
La constitution d'une base de figures-clés rend par ailleurs
incontournable un travail sur les « mots » et ce qu'ils peuvent
évoquer, car, avoir assimilé une propriété,
c'est être capable d'associer une figure-clé et un énoncé.
L'inconvénient majeur réside dans le fait que, si l'élève ne reconnaît
pas la figure-clé (si la mise en évidence de la figure-clé nécessite
par exemple un enrichissement ou un appauvrissement de la figure),
il ne peut poursuivre sa démarche de raisonnement. Il lui faut
donc d'autres possibilités d'analyse pour franchir l'obstacle.
Projet de document d'accompagnement - Juillet 2007
3. La propriété du trapèze
3.a. Calcul de l'aire de deux triangles
Propriété du trapèze :
deux triangles de
même
aire inscrits dans un trapèze
Deux triangles qui ont une même base et des sommets
sur une parallèle à la base sont d'aires égales.
En effet, les triangles ont même base [AB] et même
hauteur de longueur AH, leurs aires sont égales à
![]() base × hauteur.
base × hauteur.
3.b. Application : Théorème du papillon dans un trapèze
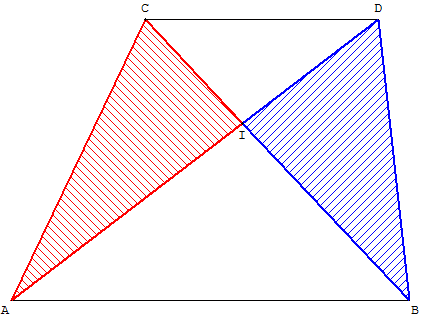
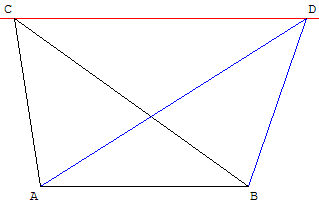
ABCD est un trapèze tel que (CD)//(AB).
Les diagonales se coupent en I.
Théorème du papillon : les aires des deux
triangles hachurés ADI et BCI sont égales.
Démonstration : aux triangles ABC et ABD
d'aires égales, enlever le triangle ABI.
![]() Dans un cercle : théorème du papillon
Dans un cercle : théorème du papillon
3.c. Démonstration par découpage
Transformation du triangle ABC en ABD
par l'intermédiaire d'un parallélogramme
Cas où la parallèle à (BD) passant par C coupe (AB) entre A et B (CD < AB).
Démonstration de la propriété du trapèze
Soit I, J, K et L les milieux des côtés [AC], [BC], [AD] et [AD].
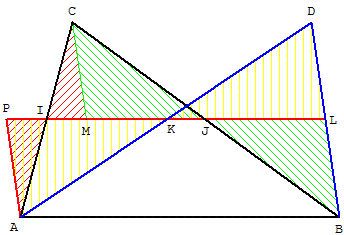
La parallèle à (BD) passant par C coupe [IJ] en M.
Par symétrie de centre I, le triangle ICM est transformé en IAP,
la symétrie de centre J, transforme le triangle JCM en JBL.
APLP est un parallélogramme
(côtés opposés parallèles) de même aire que le triangle ABC.
K est le milieu de [PL], car dans le parallélogramme PL = AB
et KL = ![]() AB avec la droite [KL] des milieux du triangle ABD.
AB avec la droite [KL] des milieux du triangle ABD.
Par symétrie de centre K, le triangle KAP est transformé en KDL,
le parallélogramme a même aire que le triangle ABD.
En conclusion, les triangles ABC et ABD ont même aire,
celle du parallélogramme ABLP.
Application :
3.d. Aire d'un triangle dans un pentagone
inscrit dans un rectangle
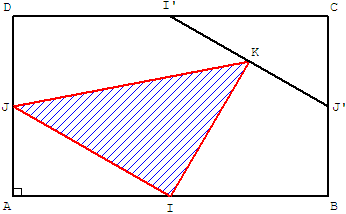
Les points I, J, I’, J’ sont les milieux des côtés d'un rectangle ABCD.
K est le milieu de [I’J’].
Quelle fraction de l'aire du rectangle représente l'aire du triangle IJK ?
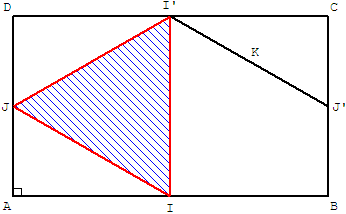
(I’J’) est parallèle à (JI). En déplaçant K en I’
on obtient le triangle IJI’ d'aire égale.
Ce triangle a une aire égale à la moitié du rectangle AII’D.
Soit le quart de l'aire du rectangle ABCD.
Les accrocs de la méthode du trapèze pourraient encore
déplacer le sommet J en A et obtiendraient
le triangle AII’ d'aire ![]() du rectangle.
du rectangle.
4. Aire et médiane
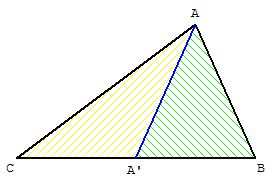
Classe de 5e
Une médiane
partage un triangle
en deux triangles
d'aires égales.
Si (AA’) est une
médiane du triangle
ABC, les triangles
ABA’ et ACA’ ont des bases de même longueur
et la même hauteur. Leurs aires sont égales.
Réciproquement : soit A’ un point du côté [BC] ;
(AA’) est une médiane du triangle ABC
si les triangles ABA’ et ACA’ ont même aire.
5. La propriété des proportions
5.a. Les aires de deux triangles contigus, inscrits dans
un même triangle, sont proportionnelles à leurs bases.
Si A’ est un point du côté [BC] d'un triangle ABC,
le rapport des aires des triangles ABA’ et ACA’
est égal au rapport de ![]() leurs bases.
leurs bases.
Aire du triangle ABA’, inscrit dans le triangle ABC
Le rapport des aires des triangles ABA’ et ABC
est égal au rapport de leurs bases BA’ et BC :
| Aire(ABA’) | BA’ | |
| = | ||
| Aire(ABC) | BC |
Barycentre : A’ est le barycentre des points
pondérés (B, A’C) et (C, A’B).
A’ est aussi le barycentre des points pondérés
(B, Aire(AA’C)) et (C, Aire(AA’B)).
5.b. Aires de triangles inscrits dans le triangle
Triangles inscrits dans ABC, ayant un ou deux côtés communs
En appliquant deux fois la propriété des proportions,
pour le triangle ABA’ inscrit dans ABC,
puis pour AB’A’ inscrit dans ABA’ on trouve :
Le rapport des aires des triangles AB’A’ et ABC est alors :
| Aire(AB’A’) | BA’ | AB’ | ||
| = | × | |||
| Aire(ABC) | BC | AB |
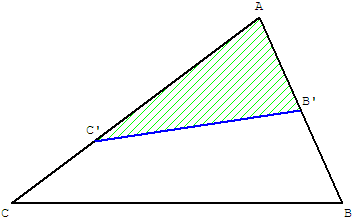
En appliquant deux fois la propriété des proportions,
par exemple pour le triangle AB’C inscrit dans ABC,
puis pour AB’C’ inscrit dans AB’C on trouve :
Le rapport des aires des triangles AB’C’ et ABC est :
| Aire(AB’C’) | AB’ | AC’ | ||
| = | × | |||
| Aire(ABC) | AB | AC |
Application :
5.c. triangle inscrit dans un triangle
Les Éléments d'Euclide - Livre IV

Chaque côté d'un triangle DEF est partagé,
par les milieux A, B et C, en segments de longueur égale.
Quelle fraction de l'aire du triangle DEF représente l'aire du triangle ABC ?
Indications
Calculer les aires des trois triangles complémentaires de ABC dans DEF.
Cette figure pour partager un triangle en 4 triangles d'aires égales
![]() Figure interactive dans GeoGebraTube : triangle médian
Figure interactive dans GeoGebraTube : triangle médian
Page suivante, voir : triangle et cercle inscrits dans un triangle équilatéral
Avec GéoPlan
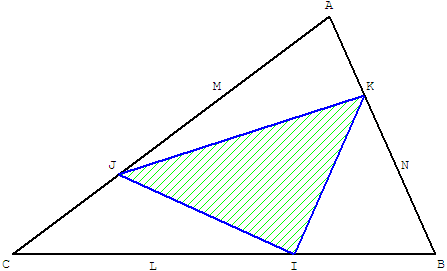
Triangle dont les côtés sont partagés en 3.
AJ = ![]() AC, AK =
AC, AK = ![]() AB, d'où :
AB, d'où :
Aire(AJK) = ![]() ×
× ![]() × Aire(ABC) =
× Aire(ABC) = ![]() Aire(ABC).
Aire(ABC).
Même résultat pour les aires des triangles BIK et CIJ.
Par soustraction de ces trois aires de l'aire du triangle ABC on en déduit que :
Aire(IJK) = ![]() Aire(ABC).
Aire(ABC).
Avec GeoGebra : les points sont mieux marqués…
Triangle dont les côtés sont partagés en 4
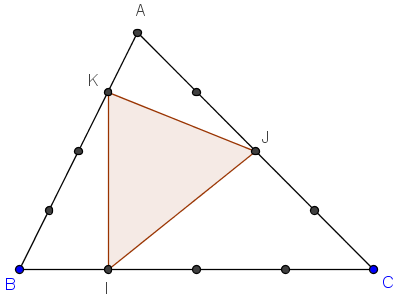
Aire(AJK) = ![]() ×
× ![]() × Aire(ABC) =
× Aire(ABC) = ![]() Aire(ABC).
Aire(ABC).
Aire(BIK) = ![]() ×
× ![]() × Aire(ABC) =
× Aire(ABC) = ![]() Aire(ABC).
Aire(ABC).
Aire(CIJ) = ![]() ×
× ![]() × Aire(ABC) =
× Aire(ABC) = ![]() Aire(ABC).
Aire(ABC).
Par soustraction de ces trois aires de l'aire du triangle ABC on en déduit que :
Aire(IJK) = ![]() Aire(ABC).
Aire(ABC).
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
aire du triangle inscrit égale aux 5/16 de l'aire du triangle circonscrit
Généraliser ces exercices à n'importe quels découpages
des côtés du triangle ABC :
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
aire du triangle inscrit égale aux 7/16 de l'aire du triangle circonscrit
5.d. Théorème du chevron
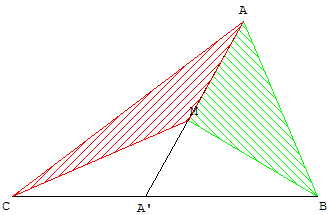
Si M est un point à l'intérieur d'un triangle ABC et A’
le point d'intersection de (AM) et de (BC),
alors le rapport des aires des triangles ABM et ACM
est égal au rapport ![]() .
.
Ce résultat se démontre par un calcul de proportions
en appliquant deux fois la propriété des proportions !
Il reste valable si M est à l'extérieur du triangle ABC.
Chevron et médiane
Si M est un point à l'intérieur d'un triangle ABC,
les triangles ABM et ACM ont même aire si
et seulement si M est sur la médiane issue de A.
5.e. Barycentre
Soit M un point à l'intérieur d'un triangle ABC,
tel que la cévienne (AM) coupe le côté (BC) en A’,
la propriété des proportions permet de vérifier que A’
est le barycentre des points pondérés
(B, Aire(A’AC)) et (C, Aire(A’AB)) ;
A’ est aussi le barycentre des points pondérés
(B, Aire(A’MC)) et (C, Aire(A’MB)).
Par différence : Aire(MAB) = Aire(A’AB) - Aire(A’MB).
Même calcul pour Aire(MAC). On en déduit que :
A’ est le barycentre des points pondérés (B, Aire(MAC)) et (C, Aire(MAB)).
Prolongement :
M est le barycentre des points pondérés
(A, Aire(MBC)) ; (B, Aire(MAC)) et (C, Aire(MAB)).
Preuve par associativité : la droite (AM) coupe le côté
(BC) en A’ qui est, selon la propriété précédente,
le barycentre partiel des deux points
(B, Aire(MAC)) et (C, Aire(MAB)),
en raison de la même propriété, la droite (BM) coupe
le côté (AC) en B’ qui est le barycentre des points
(A, Aire(MBC)) et (C, Aire(MAB)).
M, point d'intersection des droites (AA’) et (BB’),
est bien le barycentre de
(A, Aire(MBC)) ;
(B, Aire(MAC)) et (C, Aire(MAB)).
Ce résultat se généralise au cas où le point M serait à
l'extérieur du triangle ABC, en comptant négativement
les aires entièrement extérieures au triangle ABC.
Application :
5.f. Centre du cercle inscrit comme barycentre
I est le centre du cercle inscrit au triangle ABC.
On note a = BC, b = AC et c = AB.
I est le barycentre des points pondérés (A, a) ; (B, b) et (C, c).
Indications
Les trois bissectrices (intérieures) d'un triangle ABC
sont concourantes au point I, centre du cercle inscrit
dans le triangle (tangent intérieurement aux trois côtés du triangle).
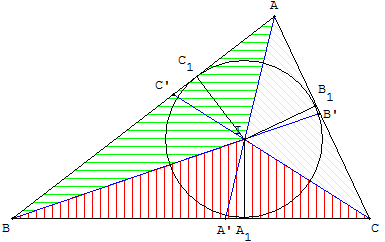
Soit A1 est la projection orthogonale de I sur (BC),
B1 sur (AC), C1 sur (AB).
IA1, IB1 et IC1 sont trois hauteurs des triangles IBC,
IAC et IAB et ont même longueur égale à
r, rayon du cercle inscrit dans le triangle ABC.
I est le barycentre des points pondérés
(A, Aire(IBC)) ; (B, Aire(IAC)) et (C, Aire(IAB))
d'après la propriété du barycentre de trois points ci-dessus.
Comme : Aire(IBC) = ![]() ar, Aire(IAC)) =
ar, Aire(IAC)) = ![]() br et Aire(IAB) =
br et Aire(IAB) = ![]() cr,
cr,
en divisant les coefficients par ![]() r,
r,
on en déduit que I est bien le barycentre des
points pondérés (A, a) ; (B, b) et (C, c).
![]() Figure interactive dans GeoGebraTube : formule des aires
Figure interactive dans GeoGebraTube : formule des aires
5.g. Formule des aires
Avec la décomposition ci-dessus du triangle ABC en trois triangles
IAB, IBC, ICA de sommet I et de hauteurs IC1, IA1, IB1
de même longueur r, le rayon du cercle inscrit, l'aire S du
triangle ABC est alors
S = ![]() ar +
ar + ![]() br +
br + ![]() cr =
cr = ![]() (a + b + c) × r = p × r.
(a + b + c) × r = p × r.
Donc S = p r et r = ![]() =
= ![]() .
.
5.h. Les trois médianes sont concourantes
Démonstration du concours des 3 médianes d'un
triangle
avec les aires, basée sur la transitivité de l'égalité :
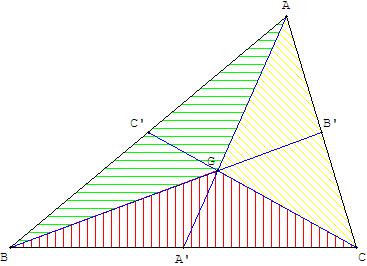
Soit G le point d'intersection des médianes [AA’] et [BB’] d'un triangle ABC.
G est sur [AA’] donc d'après la propriété ci-dessus Aire(ACG) = Aire(ABG) ;
de même, G est sur [BB’], donc Aire(ABG) = Aire(BCG).
On en déduit : Aire(ACG) = Aire(BCG) d'où, d'après la réciproque
de la propriété ci-dessus, G est sur la médiane [CC’] et les
médianes sont concourantes en G centre de gravité du triangle.
Les trois triangles ABG, BCG et ACG sont d'aires égales :
le centre de gravité d'un triangle le partage en trois triangles
de même aire.
Corollaire : [GA’] est la médiane de GBC, les triangles
GA’B et GA’C ont même aire. On en déduit que
G permet le partage du triangle ABC en six triangles d'aires égales.
![]() Figure interactive dans GeoGebraTube : médianes d'un triangle
Figure interactive dans GeoGebraTube : médianes d'un triangle
5.i. Chevron et parallélogramme
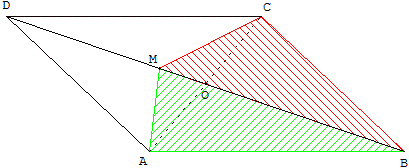
Si M est un point de diagonale [BD] d'un parallélogramme
ABCD, les triangles ABM et BCM ont même aire.
En effet, M est un point de la médiane (BO) du triangle ABC.
6. Partage en deux d'un triangle
(Olympiades 2004 Classe de quatrième
Soit un triangle ABC et un point P de [AC] tel que PA = 2PC.
Une droite variable pivotant autour du point P,
coupe un des deux autres côtés [AB] ou [BC] en M.
Le segment [MP] partage l'intérieur du triangle ABC en deux parties.
Pour quelle position de M les deux parties ont-elles des aires égales ?
Cas particulier d'un exercice des olympiades de Montpellier en 2004
Déplacer le point M sur les côtés [AB] et [BC].
Ne pas dépasser A ou C.
Soit I le milieu de [AC].
Montrer que la droite, passant par P, qui divise ABC
en deux parties d'aires égales coupe l'un des côtés
[AB]
ou [AC] en un point M tel que (MI) est parallèle à (BP).
Solution
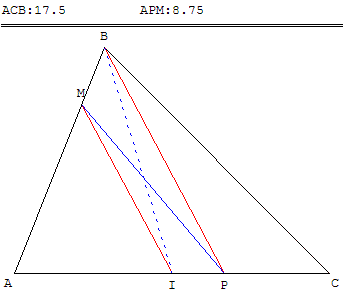
Si comme sur la figure ci-dessus le point M est sur le côté [AB] on a :
Aire(APM) = Aire(AIM) + Aire(IPM)
= Aire(AIM) + Aire
(IBM) (IPM et IBM ont même aire d'après la propriété du trapèze)
= Aire(ABI)
= ![]() Aire(ABC)
Aire(ABC)
(car la médiane [BI] partage ABC en deux triangles d'aires égales).
Exercices : étudier le cas ou l'aire du triangle MPA
est le tiers de l'aire du triangle ABC ; le quart ?
Voir : partage d'un triangle en deux polygones en terminale S.
7. Pliage d'un triangle selon les droites des milieux
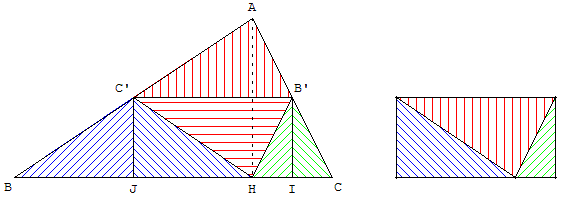
Plier un triangle ABC suivant la droite des milieux (B’C’).
Classe de 4e
Pour cela, ayant découpé le triangle ABC dans une feuille de papier,
rabattre le point A en H, pied de la hauteur issue de A.
Il est possible de trouver la hauteur par pliage en faisant glisser
le point C sur le segment [BC], en superposant les deux bords
et en marquant le pli lorsque celui-ci passe par A.
Rabattre ensuite les points B ou C en H. On obtient un rectangle.
Dans ce rectangle on retrouve la somme des angles
du triangle égale à l'angle plat IHJ, soit 180°.
L'aire du triangle est le double de l'aire de ce rectangle d'où la formule :
Aire(ABC) = 2 B’C’ × B’I = 2 × ![]() BC ×
BC × ![]() AH
AH
= ![]() base × hauteur
base × hauteur
Autre calcul de la somme des angles, voir : triangle au collège
8. Transformer un quadrilatère
en un triangle
Calculs d'aires d'un quadrilatère inscrit dans un triangle,
en le transformant en un triangle inscrit de même aire
Olympiades 2008 - Amiens
1) Question préliminaire :
Soit deux triangles MNP et MNP’ tels que (PP’)
soit parallèle à (MN)
. Démontrer que ces deux triangles ont la même aire.
2) Chaque côté d'un triangle T est partagé
en 4 segments de longueur égale.
On construit des polygones D1, D2, T3 et T4
comme indiqué sur la figure. ci-dessous.
Voici quatre « photos » de ce triangle
(en pointillés) et des polygones D1, D2, T3 et T4.
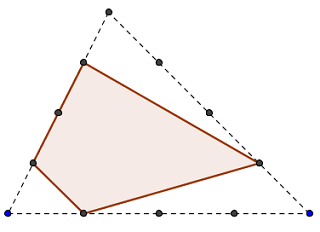
Polygone D1
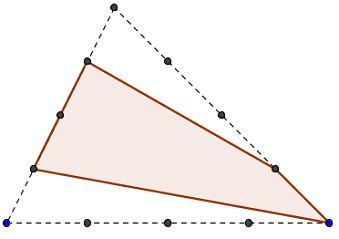
Polygone D2
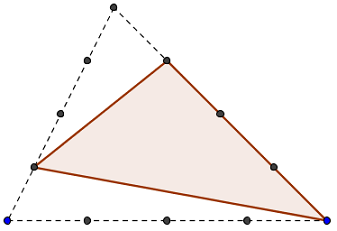
Triangle T3
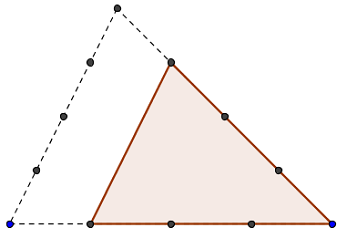
Polygone T4
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
transformer un quadrilatère en triangle
a) Montrer de proche en proche
que D1, D2, T3 puis T4 ont des aires égales.
b) En déduire le rapport :
| Aire(D1) |
| Aire(T) |
Indications
1) On demande la démonstration de la propriété du trapèze :
le parallélisme de (MN) et (PP’) implique que les
deux triangles MNP et MNP’ ont même base.
Comme ils ont même base, ils ont même aire.
2) L'énoncé imposait une démonstration un peu délicate
basée sur le choix non judicieux de transformer le triangle
MQN en MQC.
Nous ferons la démonstration avec la transformation du triangle
MQN en MQB.
Par la propriété du trapèze, ces deux triangles ont même aire.
Le polygone D1 a même aire que le triangle S2.
Au niveau de la classe de première, la démonstration est alors terminée.
En effet, d'après la propriété des proportions on a :
| Aire(BQL) | BL | AQ | 3 |
3 | 9 |
|||||
| = | × | = | × | = | ||||||
| Aire(T) | BA | AC | 4 | 4 | 16 |
Au collège, en s'inspirant de l'énoncé on terminera par la
transformation du triangle BLQ en BLP. Par la propriété
du trapèze ces deux triangles ont même aire et comme
(LP) est parallèle à (AB) on a :
| Aire(BLP) | BL | BP | 3 | 3 | 9 |
|||||
| = | × | = | × | = | ||||||
| Aire(BAC) | BA | BC | 4 | 4 | 16 |
Les triangles BLP et BQL ont même aire que D1 et on a :
| Aire(D1) | 9 |
|
| = | ||
| Aire(T) | 16 |
Version simplifiée
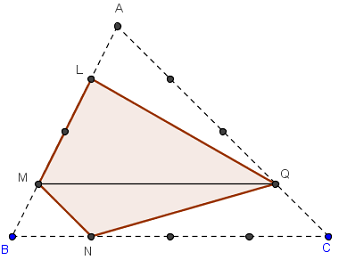
transformation directe du quadrilatère D1 en un premier
triangle S2,
puis conclusion avec un deuxième triangle S3.
Quadrilatère D1
Par la propriété du trapèze dans MQNB,
les triangles MQN et MQB ont même aire.
En ajoutant l'aire du triangle MLQ,
le quadrilatère MNQL et le triangle NBQ ont même aire.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
transformer un quadrilatère en triangle (
version avec un seul quadrilatère)
Triangle S2
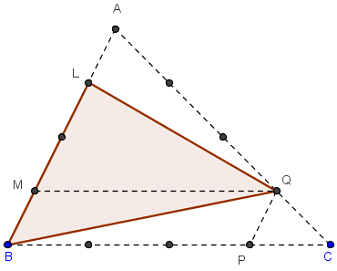
Par la propriété du trapèze dans BPQL,
les triangles LBQ et LBP ont même aire.
Triangle S3
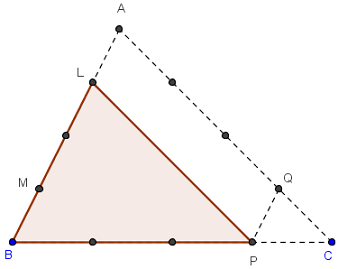
Le triangle LBP est homothétique du triangle ABC dans le rapport 3/4.
L'aire du quadrilatère est égale aux (3/4)² = 9/16 de l'aire du triangle ABC.
8.2. Quadrilatère du géoplan 5 × 5
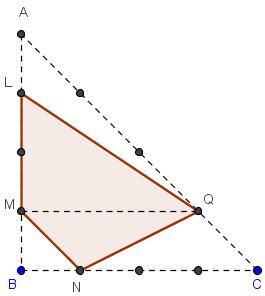
En CM2 et au début du collège il est possible de
réaliser cet exercice avec un triangle T isocèle
rectangle dans un géoplan 5 × 5.
Les figures peuvent alors être facilement réalisées
avec des élastiques autour des clous du géoplan.
Quadrilatère G1:
Aire(G1) = Aire(LMQ) + Aire(MNQ)
= ![]() × 3 × 2 +
× 3 × 2 + ![]() × 3 × 1 = 4,5.
× 3 × 1 = 4,5.
Triangle G2
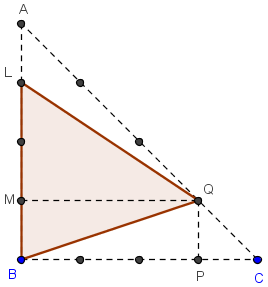
Aire(G2) = ![]() BL × QM =
BL × QM = ![]() × 3 × 3 = 4,5.
× 3 × 3 = 4,5.
Triangle G3
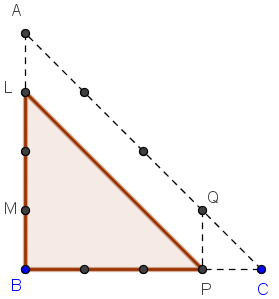
Aire(G3) = ![]() BL × BP =
BL × BP = ![]() × 3 × 3 = 4,5.
× 3 × 3 = 4,5.
![]() Figure interactive dans GeoGebraTube :
Figure interactive dans GeoGebraTube :
transformer un quadrilatère en triangle dans le géoplan
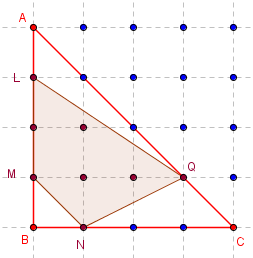
Les calculs d'aire peuvent se faire avec les carrés
unitaires et les demi-carrés :
Aire(T) = 8 ;
Aire(ALQ) = ![]() × 1 × 3 = 1,5 ;
× 1 × 3 = 1,5 ;
Aire(BNM) = ![]() ;
;
Aire(NCQ) = ![]() × 3 × 1 = 1,5 ;
× 3 × 1 = 1,5 ;
d'où Aire(G1)
= Aire(ABC) – { Aire(ALQ) + Aire(BNM) + Aire(NCQ)}
= 8 – {1,5 + 0,5 + 1,5 } = 4,5
et on a bien Aire(G1) = Aire(T) × ![]() .
.
![]() Cocher la case Géoplan 5 × 5 dans la figure
Cocher la case Géoplan 5 × 5 dans la figure
GeoGebraTube référencée ci-dessus.
8.3. Théorème de Pick
On peut aussi calculer l'aire du quadrilatère MNQL avec la formule
Aire(G1) = i + ![]() b – 1,
b – 1,
où i = 3 est le nombre de points de la grille à l'intérieur
du quadrilatère et b = 5 le nombre de points sur le bord du quadrilatère,
soit Aire(G1) = 3 + ![]() × 5 – 1 = 4,5.
× 5 – 1 = 4,5.
Table des matières
Dans d'autres pages du site
Collège : Calcul d'aires
![]() Google friendly : sur ordinateur, cette page pour grand écran
Google friendly : sur ordinateur, cette page pour grand écran
|
Page no 130, réalisée le 6/12/2008 |