Descartes et les Mathématiques

Épreuve pratique de terminale S supprimée

Sujets de 2007 réalisés avec un logiciel de géométrie dynamique

Banque de sujets de géométrie plane proposés par ÉduSCOL en 2007.

Banque de sujets 2007

2. Recherche d'un lieu géométrique

3. Évacuation des eaux

12. a. L'échelle glisse contre un mur

       b. L'équerre contre un mur

13. Lieu de l'orthocentre

21. Équation différentielle et méthode d'Euler

26. Barycentre

27. Aire maximale d'un triangle isocèle de périmètre fixé

30. Famille de cercles

31. Tangentes à une parabole

47. Partage d'un triangle

Expérimentation 2006-2007

Le groupe de mathématiques de l'Inspection générale expérimente, pendant l'année scolaire 2006/2007, la mise en place d'une épreuve pratique de mathématiques au baccalauréat S.

Ci-dessous la liste des « descriptions » et « fiches élèves » retenues en 2007 en géométrie plane. Les sujets de géométrie dans l'espace se trouvent dans la page : l'épreuve pratique avec GéoSpace

Technique GéoPlan : dans plusieurs sujets est utilisée une seule figure avec deux cadres : le cadre de gauche pour la figure géométrique, le cadre de droite pour la fonction.

2. Recherche d'un lieu géométrique

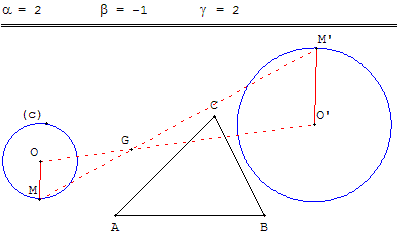
Dans le plan (P), on donne quatre points O, A, B et C et un cercle (Γ) de centre O.
Le point M est un point quelconque variable sur le cercle (Γ).

On lui associe l'unique point M’ du plan (P) défini par l'égalité : = α + β + γ où α, β, γ sont des réels donnés.

1. Il s'agit de déterminer, dans un cas particulier, le lieu géométrique (L) du point M’ lorsque le point M décrit le cercle (Γ).

• À l'aide d'un logiciel de géométrie plane construire les points O, A, B et C, le cercle (Γ) et un point variable M sur ce cercle.
  Construire le point M’ associé à M.
• En observant plusieurs positions du point M faire une conjecture sur la nature de la transformation du plan qui transforme M en M’ ainsi que la nature du lieu géométrique du point M’.

2. (a) Déterminer par le calcul la nature de la transformation du plan qui transforme le point M en le point M’.
(b) Déterminer le lieu géométrique (L) du point M’.

Production demandée

• La figure réalisée avec le logiciel de géométrie dynamique.
• Le calcul permettant d'obtenir la nature de la transformation.
• La caractérisation du lieu géométrique de M’ et sa justification.

Télécharger la figure GéoPlan lieu_barycentre.g2w

3. Évacuation des eaux - Optimisation d'une longueur

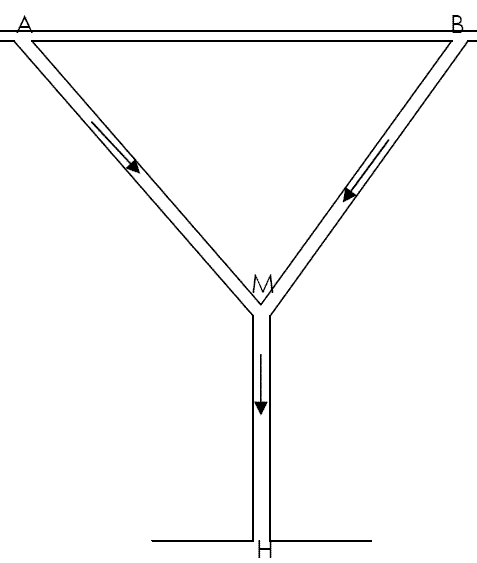
On décide de mettre en place un système de collecte des eaux de pluie sur un mur aveugle, à l'arrière de la façade d'une maison.

Sur ce mur, de forme rectangulaire, deux tuyaux obliques doivent récupérer les eaux de pluie pour les déverser dans un tuyau vertical aboutissant à un réservoir.
On donne ci-contre le plan de ce mur.

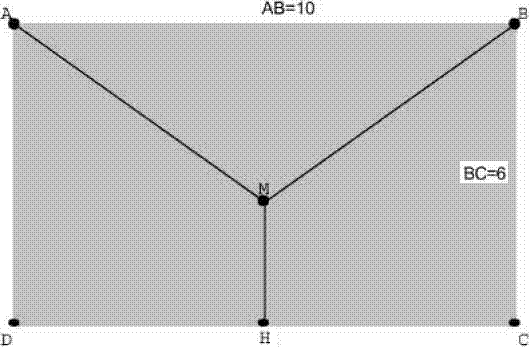
On le schématise par la figure ci-contre, où les distances sont exprimées en mètres :

Sur ce plan, la droite (MH) est la médiatrice de [DC].
Il s'agit de trouver, sur le mur de cette maison, la position du point M qui minimise la longueur totale des tuyaux.

On note Q la projection de M sur (BC) et on prend comme variable la mesure en radian de l'angle aigu BMQ = θ.

Optimisation d'une longueur : travail demandé

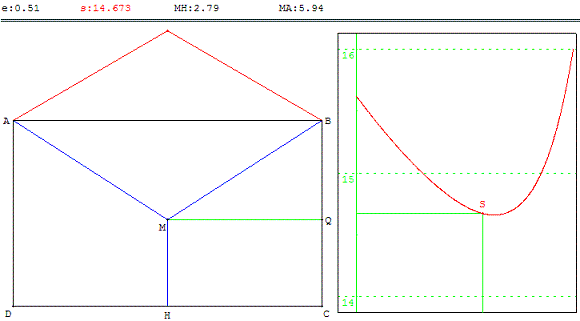
1. À l'aide du logiciel GéoPlan, ouvrir la figure « optimisation.g2w ». Elle comprend le repère R de centre D, ainsi qu'un second repère de centre I.
Construire le rectangle ABCD, puis définir la médiatrice de [DC] ainsi que le point variable M sur cette droite.
Définir la variable numérique s égale à la somme MA + MB + MH ainsi que e égale à la valeur en radian de l'angle BMQ, puis l'affichage de ces deux valeurs.

(Facultatif) : Représenter dans le repère d'origine I le point S d'abscisse e en choisissant des coordonnées adaptées.

À l'aide de la figure ainsi conçue, déterminer une valeur approchée de la mesure de l'angle BMQ en radian qui donne une somme s minimale, ainsi que la valeur approchée de cette somme.

2. On définit la fonction g : θ → g(θ) = 2MA + MH sur l'intervalle [0, ].
(a) on note g’ la dérivée de g. Démontrer que g’(θ) = 5 × .
(b) déterminer la valeur exacte de θ qui minimise la longueur des tuyaux.

Indications

MQ = MB cos θ, d'où MA = MB = = .
= tan θ, d'où BQ = MQ tan θ = 5 tan θ ; MH = QC = BC – BQ = 6 – 5 tan θ.

g(θ) = 2MA + MH = + 6 – 5 tan θ = .

La dérivée g’ est nulle si 2 sin θ –1 = 0 ; sin θ = ; θ = . g(θ) = 5 + 6 ≈ 14,66.

Télécharger la figure GéoPlan evacuation_eaux.g2w

12. Problèmes de lieux

12.a. Échelle glissant contre un mur vertical

Comment trouver le lieu du milieu d'une échelle posée contre un mur ?

Déplacement du milieu d'une échelle

Classe de quatrième

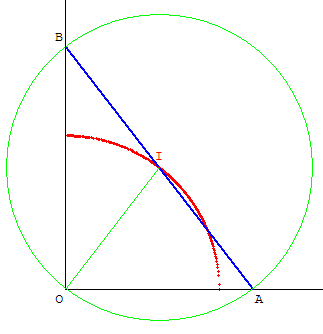
On déplace une échelle [AB] en « faisant glisser » les extrémités :
Le pied A sur le sol et le haut B sur un mur vertical.

Le lieu du milieu I de [AB] est un quart de cercle de centre O de rayon égal à la moitié de la longueur de l'échelle.

Indication

OAB un triangle rectangle et le segment [IO] est la médiane de ce triangle, issue de l'angle droit, médiane égale à la moitié de la longueur de l'hypoténuse [AB].

Télécharger la figure GéoPlan equerre2.g2w

Compétences mathématiques
Exploiter les propriétés du triangle rectangle :
  – Le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse, d'où la longueur de la médiane issue de l'angle droit.

En classe de cinquième, on inscrit le triangle rectangle AOB dans un rectangle AOBC et on exploite les propriétés des diagonales.

échelle contre un mur
      Figure interactive dans GeoGebraTube : échelle contre un mur

Problème de Pappus - échelle appuyée contre un mur

Dans un repère Oxy, on considère un carré OIJK de côté a avec I sur [Ox) et J sur [Oy). Une échelle de longueur l, passant par J, est posée en A sur la demi-droite [Ox) et s'appuie en B sur la demi-droite [Oy).
Déterminer la position de cette échelle : cela revient à calculer OA et OB en fonction de a et l.

Lieu d'un barreau de l'échelle

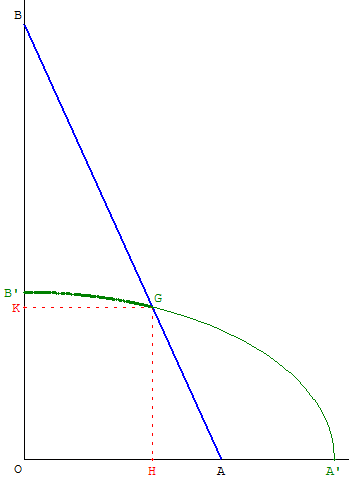
Étudier le lieu d'un point G situé sur le segment [AB].

Dans ce cas particulier, le point G est le barycentre
des points pondérés (A, 1-k) et (B, k) ; avec k ≠ 0.

On trouve un quart d'ellipse comme lieu du point G.

Télécharger la figure GéoPlan echelle_contre_mur.g2w

Démonstration analytique - Université

On note a l'abscisse de A, b l'ordonnée de B et l la longueur de l'échelle. Dans le triangle rectangle OAB, on a la relation de Pythagore a² + b² = l².

Soit G(x, y) un point fixe de l'échelle tel que AG = k AB (0 < k < 1).

Soit H(x, 0) et K(0, y) les projections de G sur les axes.
On a y = kb et x = (1 - k)a ; d'où a = x/(1 - k) et b = y/k.

Par substitution dans la relation de Pythagore on a x²/(1 - k)² + y²/k² = l²,
soit x²/((1 - k)l)² + y²/(kl)² = 1, équation d'une ellipse de sommets A’ et B’ où A’ est le point de [OA) tel que OA’ = (1 - k)l et B’ le point de [OB) tel que OB’ = kl.

Lieux des barreaux d'une échelle

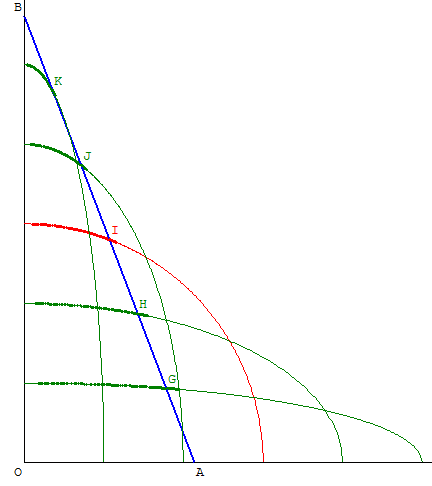
Échelle à cinq barreaux

Une échelle, de longueur 6, a cinq barreaux.

On représente les lieux des cinq barreaux à partir des points :

G barycentre des points pondérés (A, 5) et (B, 1),
H barycentre des points pondérés (A, 4) et (B, 2),
I milieu de [AB],
J barycentre des points pondérés (A, 2) et (B, 4),
K barycentre des points pondérés (A, 1) et (B, 5).

Les trajectoires sont des arcs d'ellipses.

Télécharger la figure GéoPlan echelle_contre_mur2.g2w

12.b. L'équerre contre un mur

On s'intéresse à l'étude du lieu de certains points de l'équerre lorsque l'on fait glisser le sommet A sur le sol et le point B contre un mur.

Classe de seconde

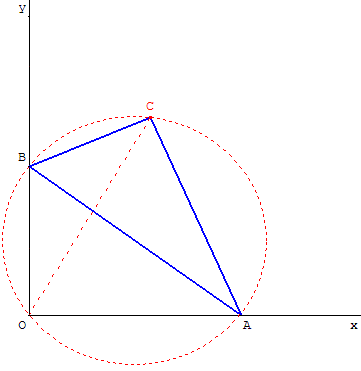
Une équerre ABC, rectangle en C, est placée de telle façon que le point A est un point variable du demi-axe des abscisses [Ox) et le point B est sur le demi-axe des ordonnées [Oy).

On déplace l'équerre en « faisant glisser » A et B sur les axes.

Montrer que le point C se déplace sur une droite issue du point O.

Indication

BCA et BOA sont deux triangles rectangles inscrits dans le cercle de diamètre [BA]. Les angles inscrits AOC et ABC dans ce cercle sont égaux. Le point C se trouve sur la droite fixe passant par O faisant un angle égal à ABC avec l'axe (Ox).

Le lieu L du point C est un segment porté par cette droite.

Télécharger la figure GéoPlan equerre.g2w

Technique GéoPlan

Le point A étant placé sur (Ox), le point B est l'intersection de l'axe (Oy) avec le cercle de centre A et de rayon égal à la longueur l de l'équerre. Le point C est situé sur le cercle de diamètre [AB].
Si l'équerre est définie par son angle en Â, avec GéoPlan, le plus simple est de construire le point C comme image de B par une similitude de centre A et de rapport cos(Â).
Par exemple, si le triangle ABC représente une équerre telle que AB = 6, BC = 3 et l'angle en C est droit alors cos(Â) = cos() = .

Le point G de l'équerre dont on cherche le lieu est défini comme barycentre des points pondérés (A, α) ; (B, β) et (C, γ) où les coefficients α, β ou γ sont positifs.

Fiche élève

Le point I est le milieu du segment [AB]

On s'intéresse aux lieux des points I et C.

• Observer les propriétés géométriques de la figure. Avec un logiciel de géométrie, construire une figure dynamique illustrant la situation.
• Visualiser, à l'aide du logiciel, le lieu du point I quand A décrit la demi-droite [Ox). Quelle conjecture peut-on émettre sur la nature de ce lieu ?
• Visualiser, à l'aide du logiciel, le lieu du point C quand A décrit la demi-droite [Ox). Quelle conjecture peut-on émettre sur la nature de ce lieu ?

Donner les mesures des angles de l'équerre, puis celle de BÔC (B distinct de O).

• En déduire que le lieu de C est inclus dans une courbe simple, dont on précisera la nature.
• Démontrer que : OC = 6 sin(OBC).
• En déduire le lieu de C.

Cas général - Après bac

Quel est le lieu d'un point G, situé sur l'équerre ?

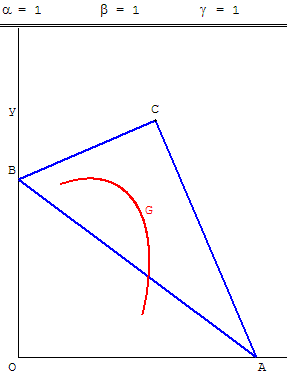
Un arc de conique ?

Télécharger la figure GéoPlan equerre3.g2w

Deux demi-ellipses

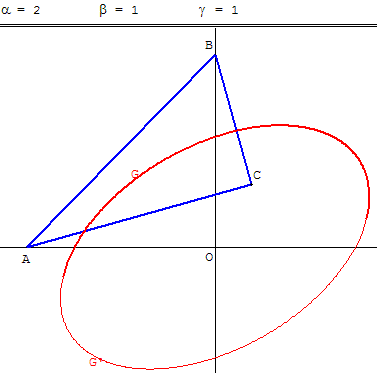
A glisse sur la droite (Ox), B glisse sur (Oy) :
On fait varier A dans un intervalle de longueur 2l autour de O.
On obtient une demi-ellipse tracée en gras.

B glisse sur (Oy’), A glisse sur la droite (Ox) :
On fait aussi glisser B sur [Oy’) en B’ et on obtient un point G’ qui se déplace sur l'autre demi-ellipse (trace fine).

Le point G se déplace sur une ellipse.

Télécharger la figure GéoPlan equerre5.g2w

Points sur les côtés de l'équerre

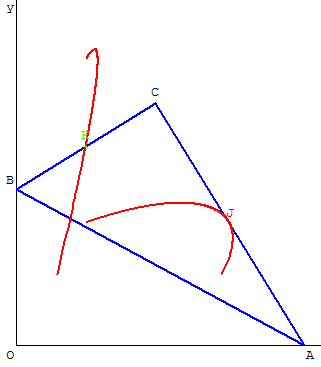
Quels sont les lieux des milieux J et K des côtés de l'équerre ?

Les lieux sont des arcs d'ellipses.

Télécharger la figure GéoPlan equerre4.g2w

Commandes GéoPlan pour le lieu géométrique :

Déplacer le point A ;
Touche T : Trace d'un point,
Touche S : Sortie du mode trace.

Touche L : afficher/cacher le Lieu géométrique,
Touche I : indication pour la solution.

Variante du problème : on remplace l'équerre par un carré mobile de côté [AB].

Compétences évaluées

Compétences TICE
  – Construire une figure avec un logiciel de géométrie dynamique ;
  – Visualiser un lieu.

Compétences mathématiques
  – Ellipse, hors programme des lycées depuis trois décennies !

13. Lieu de l'orthocentre

Recherche du lieu de l'orthocentre d'un triangle lorsque l'un des sommets se déplace sur une droite.

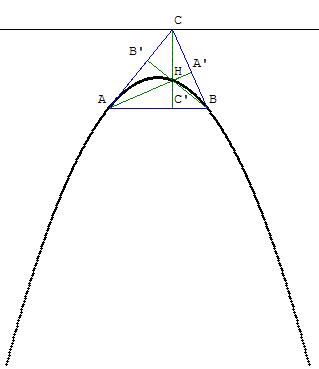
Dans le plan, ABC est un triangle d'orthocentre H.
Il s'agit de déterminer le lieu L des points H quand C se déplace sur une certaine droite.

Fiche élève

Dans le plan, ABC est un triangle quelconque.
On note K le centre de son cercle circonscrit et H son orthocentre.
On s'intéresse au lieu (L) des points H quand C se déplace sur une droite parallèle à la droite (AB).

1. (a) Faire une figure avec un logiciel de géométrie dynamique, faisant apparaître les points A et B, le point C sur une droite parallèle à la droite (AB), le triangle ABC, le point H et le point K.
Afficher la trace du point H quand C varie sur la parallèle à (AB).
Faire une conjecture concernant la nature du lieu des points H.

(e) : = + + .

2. À partir de cette question, le plan est rapporté à un repère orthonormal (O, , ) ; les points A et B sont donnés par leurs coordonnées : A(–1 ; 1) et B(1 ; 1). Le point C est sur l'axe des abscisses, et a pour abscisse un réel x.

• Demander à nouveau le lieu (L) des points H.
• Quelle en serait une équation ?

3. Vérifier la conjecture émise, en traçant le lieu des points H, grâce à son équation.

4. En admettant que K a pour coordonnées (0 ; ) et l'égalité (e) donnée à la première question en déduire les coordonnées de H puis l'équation de (L).

Indications (avec d'autres données)

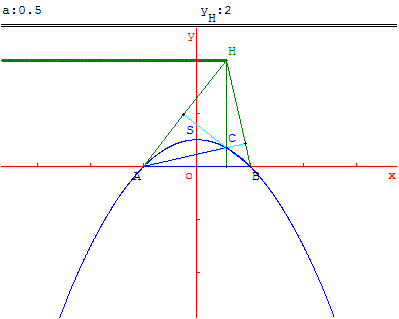
Si (d) est une droite parallèle à (AB), distincte de (AB), le lieu de l'orthocentre H, quand le sommet C parcourt la droite (d), est une courbe passant par A et B. Cette courbe est symétrique par rapport à la médiatrice de [AB]. On va montrer que c'est une parabole.

En géométrie analytique utilisons un repère (O, , ) centré en O milieu de [AB] tel que :
= et que soit un vecteur directeur de la médiatrice de [AB].

Les coordonnées des points sont alors A(–1, 0) ; B(1, 0) ; C(x, γ) et H(x, y) car H étant l'orthocentre du triangle ABC, C et H ont même abscisse x.

AH étant orthogonal à CB, le produit scalaire . = 0.

Les coordonnées des vecteurs sont (1 + x, y) ; (1 – x, –γ).

On obtient finalement avec la formule analytique du produit scalaire :

XX’ + YY’ = (1 + x) (1 – x) – γ y = 0,

soit y =       γ ≠ 0.

Cette équation prouve que H se déplace sur une parabole passant par A et B et, qui plus est, que le lieu de H est toute la parabole, étant donné que x décrit R.

Réciproquement, comme l'orthocentre du triangle ABH est le point C, on peut montrer que si C se déplace sur une parabole passant par A et B, d'axe de symétrie la médiatrice de [AB], alors le lieu de l'orthocentre est une droite parallèle à (AB).

Télécharger les figures GéoPlan dr_ortho.g2w ; pa_ortho.g2w

Voir aussi : paraboles

21. Équation différentielle et méthode d'Euler

Le but de l'exercice est de mettre en œuvre la méthode d'Euler pour une équation différentielle de type y’ = ay (où a est un réel donné) et d'en déduire une valeur approchée.

Compétences évaluées
Compétences TICE
  • Utiliser un tableur, notamment ses fonctions graphiques ;
  • Réaliser une feuille de calcul adaptée à la situation.

Compétences mathématiques
  • Mettre en œuvre les connaissances sur la méthode d'Euler ;
  • Déterminer la primitive d'une fonction, avec condition initiale ;
  • Faire le lien entre la fonction approchée obtenue par la méthode d'Euler et la primitive : évaluer une précision.

En projet, voir méthode d'Euler

26. Lieu d'un barycentre

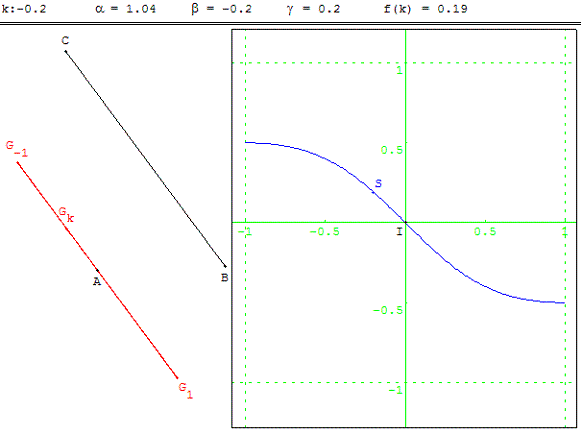
Situation

On considère A, B et C trois points non alignés du plan et k un réel de l'intervalle [–1; 1].
On note G_k le barycentre du système de points pondérés : {(A, α_k) ; (B, β_k) ; (C, γ_k)}

où α_k, β_k et γ_k sont des réels dépendants de k, de somme non nulle. Il s'agit de déterminer le lieu des points G_k lorsque k décrit l'intervalle [–1; 1].

Fiche élève

On considère A, B et C trois points du plan et k un réel de l'intervalle [–1; 1].
On note G_k le barycentre du système de points pondérés : {(A, k² + 1) ; (B, k) ; (C, – k)}.
Le but de cet exercice est de déterminer le lieu des points G_k lorsque k décrit l'intervalle [–1; 1].

1. Visualisation à l'aide d'un logiciel de géométrie :

• Construire les points A, B, C, G₁ et G_-1.
• Construire le point G_k puis visualiser l'ensemble des points G_k lorsque k décrit [–1; 1].
• Quelle est la nature de l'ensemble précédent ?

2. Justification mathématique :

• Justifier, pour tout réel k de [–1; 1] l'existence du point G_k.
• Démontrer que pour tout réel de l'intervalle [–1; 1], on a: = .
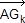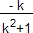
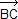• Démontrer la conjecture faite avec le logiciel. On pourra utiliser les variations de la fonction f définie sur [–1; 1] par : .

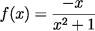Indications

D'après la fonction vectorielle de Leibniz α + β + γ = (α + β + γ) , en plaçant M en A on a :
(k² + 1) = k – k = −k et = .

La fonction f est continue et décroissante sur [–1; 1].

Télécharger la figure GéoPlan barycentre.g2w

27. Aire maximale d'un triangle isocèle de périmètre fixé

Isopérimétrie

Problème issu du mythe de la reine Didon lors la création de Carthage :
trouver la forme géométrique qui maximise son aire avec un périmètre fixé.

Énoncé

On considère un triangle ABC isocèle en A de périmètre fixé.
Le but de cet exercice est de déterminer parmi tous les triangles isocèles possibles, celui dont l'aire est maximale.

1. Expérimentation à l'aide d'un logiciel de géométrie :

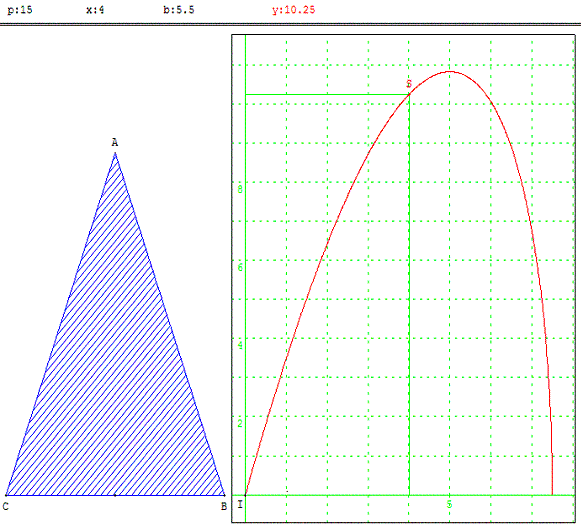
• À l'aide d'un logiciel de géométrie, construire un triangle ABC isocèle en A, dont le périmètre est fixé et exactement égal à 15.
• Parmi tous les triangles possibles, quelle semble être la nature du triangle d'aire maximale ?

2. Démonstration :

On note x la longueur BC et A(x) l'aire du triangle ABC.

• Dans quel intervalle le réel x peut-il prendre ses valeurs ?
• Soit H le milieu de [BC], exprimer AH en fonction de x et en déduire que A(x) = .
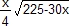• Résoudre le problème posé.

Si p = 15, x = BC = a, AB = AC = b, Aire(ABC) = y ; dans le cadre de droite est représenté le point S(x, y).

Télécharger la figure GéoPlan max_aire_tr_peri_const.g2w

Voir : maxi_mini

Aire maximale d'un triangle

30. Famille de cercles

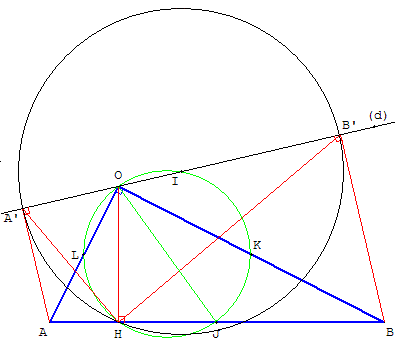
Dans le plan on considère un triangle BOA rectangle en O et une droite (d) passant par O.
On note A’ et B’ les projetés orthogonaux respectifs de A et de B sur (d).
Enfin, dans le triangle OAB, H est le pied de la hauteur issue de O.

(a) Faire une figure à l'aide d'un logiciel de géométrie.
(b) Quelle conjecture peut-on faire concernant les différents cercles (c) lorsque la droite (d) tourne autour de O ?

On considère la similitude directe S de centre H qui transforme A en O.

• Quel est l'angle de cette similitude ? Justifier que l'image de O par S est B.
• Déterminer les images par S des droites (AA’) et (d), puis celle du point A’.
• Démontrer la conjecture faite au (b).

Conjectures

Les cercles (c) passent par le point H pied de la hauteur issue de O du triangle BOA.

Dans le cercle de diamètre [OA], les angles inscrits OAH et OA’H sont égaux, de même dans le cercle de diamètre [OB], les angles inscrits OBH et OB’H sont égaux. Les triangles BOA et B’HA’ sont semblables, donc B’HA’ est un triangle rectangle en H inscrit dans le cercle de diamètre [A’B’] : (c) contient le point H.

Si J, K et L sont les milieux des côtés [AB], [OB] et [OA] les centres I des cercles (c) appartiennent au cercle de diamètre la médiane [OJ] (cercle passant par K et L).

En effet, dans le cercle (c) l'angle au centre A’IH est la moitié de l'angle inscrit A’B’H. De même, dans le cercle de diamètre [AB], l'angle au centre OJA est la moitié de l'angle inscrit OBA.
Comme dit ci-dessus les angles inscrits A’B’H = OBA sont égaux, donc les angles doubles OIH et OJH sont égaux. Les points I, J, O et H sont cocycliques. Le point I est sur le cercle diamètre [OJ].

Télécharger la figure GéoPlan famille_cercle.g2w

Voir un curieux point de concours sur la hauteur OH : produit scalaire

Compétences évaluées
Compétences TICE
  • Utilisation d'un logiciel de géométrie dynamique pour conjecturer une propriété.

Compétences mathématiques
  • Triangles semblables ;
  • Propriété de conservation d'une similitude (image d'une droite par une similitude) ;
  • Triangle rectangle inscrit dans un demi-cercle.

31. Tangentes à une parabole

En géométrie analytique du plan, on considère une parabole (C) et on étudie le point d'intersection des tangentes à (C) en deux points dont les abscisses sont liées par une relation simple.

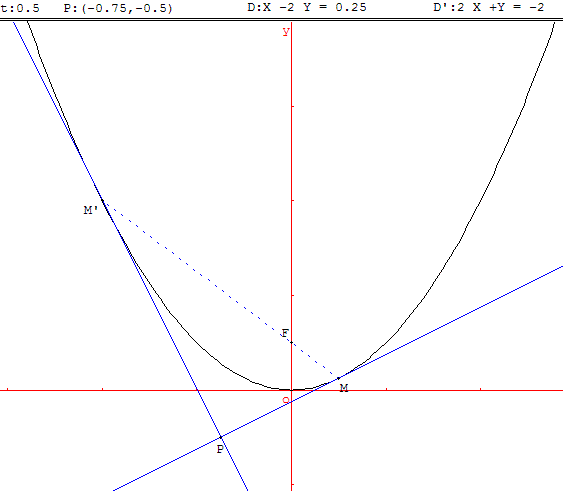
Situation

Le plan est rapporté à un repère orthonormal. On considère la parabole (C) d'équation :
y = .
Étant donné un réel t non nul, on se propose de mettre en évidence, puis de démontrer une propriété du point d'intersection des tangentes à la parabole (C) aux points M et M’ d'abscisses respectives t et t’ = − .

1. (a) À l'aide d'un logiciel adapté, tracer la parabole (C).

• On se donne un réel t. Placer le point M d'abscisse t sur la courbe (C).
• Tracer la droite (D) tangente à (C) au point M.

Indication : Si le logiciel utilisé le nécessite, calculer d'abord le coefficient directeur de cette tangente.

(b) Placer le point M’ d'abscisse t’ = − sur la courbe C. Tracer la droite (D’) tangente à (C) en M’.
Placer le point d'intersection P des droites (D) et (D’).

• Lorsque t varie dans R^*, à quel ensemble le point P semble-t-il appartenir ?

2. Démonstration

• Donner les équations des droites (D) et (D’).
• Calculer les coordonnées du point P et conclure sur la propriété conjecturée.

Remarques

1. La droite MM’ passe par un point fixe, le foyer F de la parabole.

Définition : la courbe orthoptique d'une parabole est le lieu des points d'où l'on peut mener deux tangentes à la parabole perpendiculaires entre elles, autrement dit le lieu des points d'où l'on « voit » la parabole sous un angle droit.

Pour les droites (D) et (D’), le produit des coefficients directeurs t × (–) est égal à –1 ; les deux tangentes sont perpendiculaires.
Le lieu géométrique est donc la courbe orthoptique, directrice de la parabole.

2. Démonstration

La tangente au point de coordonnées (x₀, y₀) a pour équation y = f’(x₀) (x–x₀) + f(x₀), avec f(x) = et f’(x) = x.

Pour x₀ = t, (D) a pour équation y = t(x – t) + t²/2, soit y = tx – t²/2.

Pour x₀ = –, (D’) a pour équation y = –(x + ) + 1/(2t²), soit y = –x/t – 1/(2t²).

Les coordonnées du point P d'intersection se trouvent en résolvant le système de deux équations :
y = tx – t²/2 et
y = –x/t – 1/(2t²).

Avec y = tx – t²/2, on obtient en éliminant y : tx – t²/2 = – x/t – 1/(2t²),
soit tx + x/t = t²/2 – 1/(2t²) ou tx(1 + 1/t²) = (t² – 1/t²)
et en multipliant par t² on a tx(t² + 1) = (t⁴ – 1) = (t² +1)(t² – 1), puis en simplifiant on a :
tx = (t² – 1) et
y = tx – t²/2.
Soit x = (t² – 1)/(2t)
y = – .

Le lieu des points P est inclus dans la droite horizontale, d'équation y = – .
En étudiant la fonction g(t) = (t² – 1)/(2t) sur R^+*, on remarque que g est une bijection de R^+* vers R. Tous les points de la droite sont donc dans le lieu géométrique.

Télécharger la figure GéoPlan tan_edu31.g2w

Article cité par Futura-Sciences

Paraboles

Points équidistants d'une droite et d'un point : épreuve pratique 2008

Cercles et paraboles : épreuve pratique 2008

Propriétés de la parabole : épreuve pratique 2009

Lieux géométriques

47. Partage d'un triangle en deux polygones de même aire

Dans le plan on définit un triangle ABC non isocèle en A et dont les angles en B et en C sont aigus. On note a son aire.
On appelle H le pied de la hauteur issue de A dans le triangle ABC et l'on se place dans le cas où CH > BH.

On se propose de démontrer qu'il existe une droite et une seule perpendiculaire au côté [BC], en un point M, qui partage le triangle ABC en deux polygones de même aire.

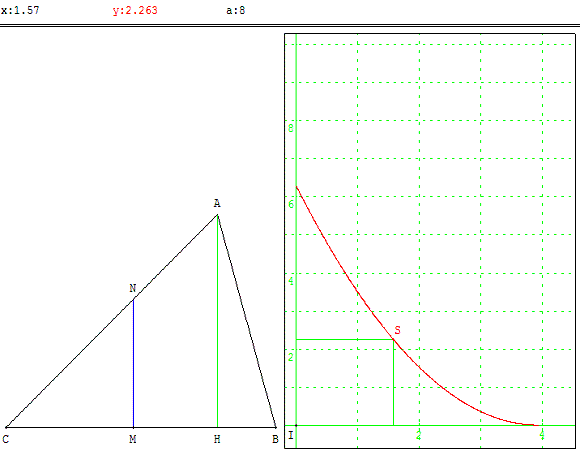
• Construire la figure demandée en utilisant un logiciel de géométrie dynamique. Déterminer, à l'aide du logiciel, la position de M en lequel la droite recherchée doit couper le segment [CH] pour répondre au problème posé.
• Étudier le cas où le point M est sur le segment [BH].
• On suppose que le point M est situé sur le segment [CH] et on pose CM = x. On appelle N le point d'intersection du segment [AC] avec la droite perpendiculaire à (BC) passant par M.

On note L la longueur du segment [CH]. On admet que la fonction f qui, à tout x de [0; L], associe l'aire du triangle CMN est continue.
On ne cherchera pas à expliciter f(x).

(a) Que traduit l'égalité f(x) = ?

• Préciser les variations de f à l'aide du logiciel. Déterminer la valeur de f(0).
• Comparer f(x) et 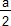quand M est en H.
• En déduire la réponse au problème posé.

Production demandée

• Figure réalisée avec emplacement du point M répondant au problème.
• Interprétation de l'égalité (a).
• Utilisation d'un théorème d'analyse.

Indications

f(0) = 0, f(L) > lorsque M est en H, comme f est continue sur [0; L], d'après le théorème des valeurs intermédiaires, il existe une valeur x pour laquelle f(x) = .
Le triangle CMN a alors une aire égale à la moitié de celle du triangle ABC.

Pour l'aire du triangle CMN solution on a : x × MN = , d'où MN = .

Les triangles rectangles NMC et AHC sont semblables, donc tan(C) = = , soit = , d'où x = .

x = CM, y = f(x) = Aire(CMN), dans le cadre de droite est représenté le point S(x, y).

Télécharger la figure GéoPlan max_aire_tr_peri_const.g2w

Table des matières

Sujets traités dans d'autres pages

Sujets de géométrie dans l'espace 2007

15. Distance de deux droites dans l'espace
19. Problème de Bergson
33. Section plane d'un tétraèdre et optimisation d'une distance

23. Plan et droite orthogonaux dans le cube

Banque de sujets 2004

4. Arc de cercle

17. Centre de deux similitudes

28. Quatre triangles équilatéraux

Banque de sujets 2005

30. Aire maximum d'un rectangle

Banque de sujets 2007

16. Modélisation d'une situation géométrique : trajet en temps minimum

Mathématiques en terminale

Épreuve pratique en TS

Géométrie plane
Sujets 2007 (cette page)

Sujets 2008

Sujets 2009

Géométrie dans l'espace
Sujets 2007 et 2008

Sujets 2009

Épreuve pratique en 2^nde : Rectangle inscrit dans un triangle

La géométrie à l'épreuve pratique de terminale S avec GéoPlan et GéoSpace

revue.sesamath Format PDF

Page n^o 108, réalisée le 1/4/2007
mise à jour le 19/1/2012