Descartes et les Mathématiques

Coniques à centre

Constructions géométriques des coniques bifocales.

E. Constructions de l'ellipse

E.0. Les coniques de la dioptrique de Descartes

Descartes s'est intéressé aux propriétés des coniques pour la confection des lentilles en optique.

Les ellipses

L'ellipse ou l'ovale est une ligne courbe que les mathématiciens ont accoutumé de nous exposer en coupant de travers un cône ou un cylindre, et que j'ai vu aussi quelquefois employer par des jardiniers dans les compartiments de leurs parterres, où ils la décrivent d'une façon qui est véritablement fort grossière et peu exacte, mais qui fait, ce me semble, mieux comprendre sa nature que la section du cylindre ni du cône.

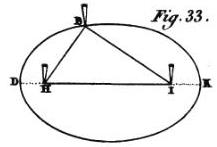
Ils plantent en terre deux piquets, comme, par exemple, l'un au point H, l'autre au point I, et, ayant noué ensemble les deux bouts d'une corde, ils la passent autour d'eux en la façon que vous voyez ici BHI ; puis, mettant le bout du doigt en cette corde, ils le conduisent tout autour de ces deux piquets en la tirant toujours à eux d'égale force, afin de la tenir tendue également, et ainsi décrivent sur la terre la ligne courbe DBK, qui est une ellipse. Et si, sans changer la longueur de cette corde BHI, ils plantent seulement leurs piquets H et I un peu plus proches l'un de l'autre, ils décriront derechef une ellipse, mais qui sera d'autre espèce que la précédente : et s'ils les plantent encore un peu plus proches, ils en décriront encore une autre; et enfin, s'ils les joignent ensemble tout-à-fait, ce sera un cercle qu'ils décriront ; au lieu que, s'ils diminuent la longueur de la corde en même proportion que la distance de ces piquets, ils décriront bien des ellipses qui seront diverses en grandeur, mais qui seront toutes de même espèce.

E.1. Image d'un cercle par affinité

Construction d'une ellipse de sommets A, A’, B, B’ ; de grand axe A’A = 2a et de petit axe BB’ = 2b.

Soit P un point du cercle (c) de centre o, et de rayon a.

Une affinité d'axe (oy), au point P(x, y₁), fait correspondre le point M(x, y) tel que y = y₁.

Avec GéoPlan, réaliser la trace du point M, avec le point P comme pilote.

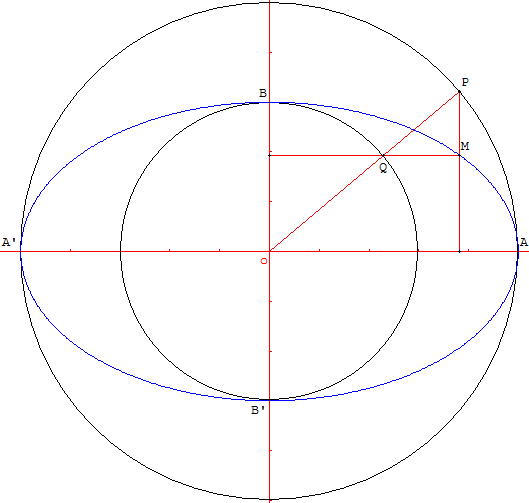
Le cercle (c) ayant pour équation x² + y₁² = a², on a donc
x² + (ay / b)² = a², d'où l'équation de l'ellipse : x²/a² + y²/b² = 1.

Soit Q un point du cercle (c’) de centre o, et de rayon b.

Une autre affinité d'axe (ox), au point Q(x₂, y), fait correspondre le point M(x, y) tel que x = x₂.

Télécharger la figure GéoPlan ellipse1.g2w

E.2. Techniques de la bande de papier

Génération mécanique de l'ellipse :

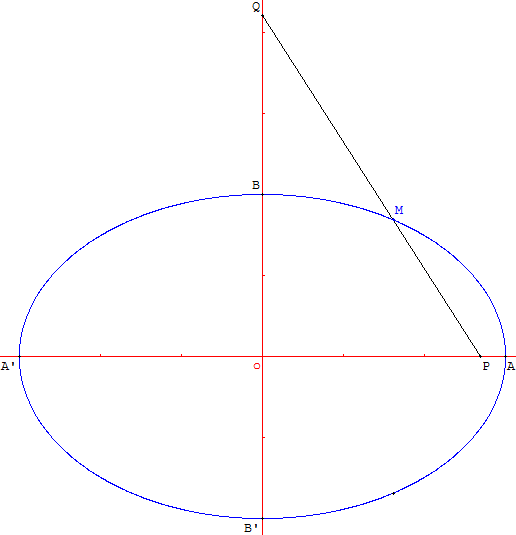
4.2.a. Sur une règle [PQ] de longueur l = a + b, on place un place un point M tel que QM = a. On déplace la règle pour obtenir le lieu du point M en plaçant P sur l'axe des abscisses et Q sur l'axe des ordonnées.

Avec GéoPlan, la trace du point M, avec le point P sur l'intervalle [L’, L] comme pilote, permet d'obtenir une demi-ellipse de sommets A, A’, B.

Par symétrie par rapport à l'axe (ox), le point M’ situé sur une règle [PQ’] tel que Q’M’ = a permet d'obtenir l'autre demi-ellipse de sommets A, A’, B’.

Télécharger la figure GéoPlan ellipse2.g2w

E.2.b. Construction d'Archimède

Tracé avec une règle percée [QM].

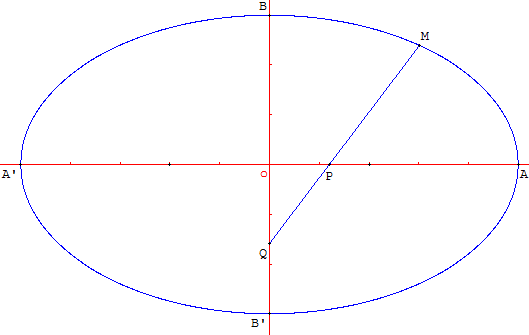
La règle est de longueur a = QM. Le point P est situé sur la règle tel que PM = b (b < a).

Le point P est astreint à se déplacer sur l'axe (Ox) entre le point P₁ d'abscisse a – b et P₂ d'abscisse b – a.

Le point Q est astreint à se déplacer sur l'axe (Oy).

Lorsque l'on déplace P et Q sur les axes, le lieu du point M est une ellipse.

Télécharger la figure GéoPlan ellipse4.g2w

E.3. Méthode du jardinier

  Définition bifocale de l'ellipse - Construction par le cercle directeur.

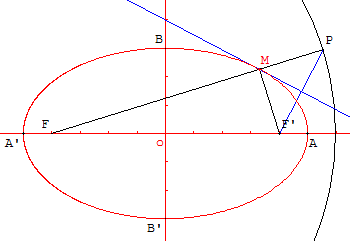
Étant deux points F et F’ dont la distance est 2c, on appelle ellipse l'ensemble des points M tels que MF + MF’ = 2a (c<a).

La construction se réalise avec le cercle directeur (c) de centre F et de rayon 2a.

Soit P un point de cercle. La médiatrice de [PF’] coupe [FP] en M, point de l'ellipse. Cette médiatrice est la tangente à l'ellipse en M.

Avec GéoPlan, réaliser la trace du point M, avec le point P comme pilote.

Remarque : on a : a² = b² + c².

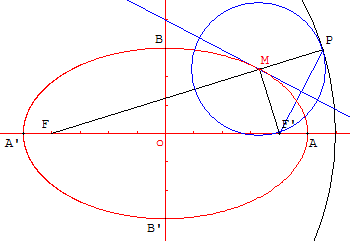
L'ellipse de cercle directeur (c) et de foyer F’ est l'ensemble des centres M des cercles tangents à (c) et passant par F’.

Télécharger la figure GéoPlan ellipse3.g2w

E.4. L'ellipse chez les Anciens

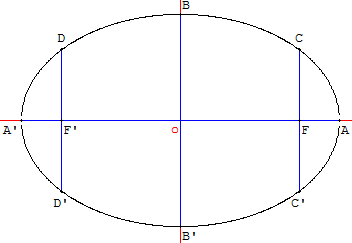
Ellipse d'équation x²/a² + y²/b² = 1 (a > b).

[AA’] est le traversant de l'ellipse de longueur 2a.

Une corde qui passe par un des foyers est une corde focale.
Chez les « anciens Égyptiens », la corde focale perpendiculaire au traversant est le côté droit de l'ellipse, on l'appelle aussi par son nom latin le latus rectum.

[CC’] est côté droit de l'ellipse de longueur 2c avec c² = a² – b² ; c >0.

Le paramètre c, demi-longueur du côté droit, est aussi nommé latus rectum.

Télécharger la figure GéoPlan ellipse4.g2w

Propriétés diamétrales des coniques

Si on coupe une conique par des droites parallèles, les milieux des cordes ainsi obtenues sont alignés, sur une droite appelée « un diamètre ».
Les diamètres des ellipses et des hyperboles passent par le centre de la conique.

Voir aussi : côté droit de la parabole

H. Étude de l'hyperbole

H.0. Les hyperboles dans la dioptrique de Descartes

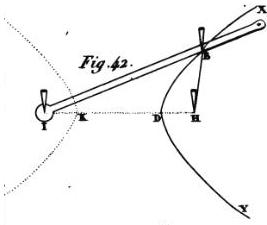
L'hyperbole est aussi une ligne courbe que les mathématiciens expliquent par la section d'un cône, comme l'ellipse ; mais, afin de vous la faire mieux concevoir, j'introduirai encore ici un jardinier qui s'en sert à composer la broderie de quelque parterre. Il plante derechef deux piquets aux points H et I ; et, ayant attaché au bout d'une longue règle le bout d'une corde un peu plus courte, il fait un trou rond à l'autre bout de cette règle dans lequel il fait entrer le piquet I, et une boucle à l'autre bout de cette corde qu'il passe dans le piquet H ; puis, mettant le doigt au point X où elles sont attachées l'une a l'autre, il le coule de là en bas jusqu'à D, tenant toujours cependant la corde toute jointe et comme collée contre la règle depuis le point X jusqu'à l'endroit où il la touche, et avec cela toute tendue, au moyen de quoi, contraignant cette règle de tourner autour du piquet I à mesure qu'il abaisse son doigt, il décrit sur la terre la ligne courbe XBI qui est une partie d'une hyperbole.

Voir aussi : hyperbole de Descartes

H.1 Étude bifocale de l'hyperbole

Étant deux points F et F’ dont la distance est 2c, on appelle hyperbole l'ensemble des points M tels que |MF – MF’| = 2a (c>a).

La construction se réalise avec le cercle directeur (c) de centre F et de rayon 2a.

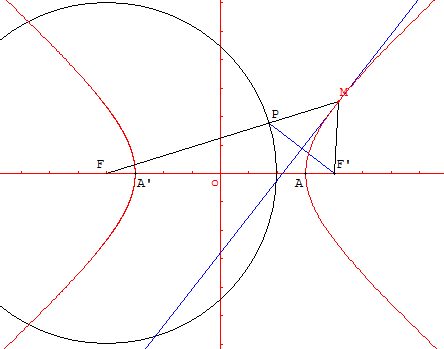
Soit P un point de cercle. La médiatrice de [PF’] coupe (FP) en M, point de l'hyperbole.
Cette médiatrice est la tangente à l'hyperbole en M. C'est la bissectrice de l'angle FMF’ des rayons focaux [MF] et [MF’] de M.

Avec GéoPlan, réaliser la trace du point M, avec le point P comme pilote.

L'hyperbole de cercle directeur (c) et de foyer F’ est l'ensemble des centres M des cercles tangents à (c) et passant par F’.

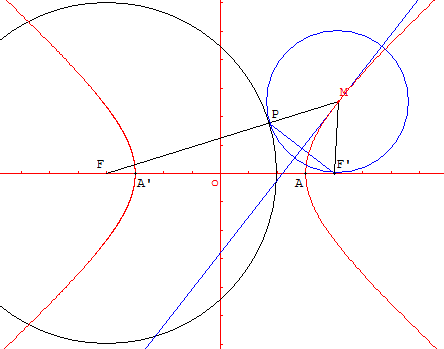
Les sommets A, A’ de l'hyperbole sont tels que A’A = 2a. (A’A), un des axes de symétrie de l'hyperbole, est appelé axe focal ou axe transverse.

Remarque : avec GéoPlan, en modifiant a ou c, on utilise la même figure pour le tracé de l'ellipse du jardinier ou pour cette hyperbole.

Télécharger la figure GéoPlan hyperbole1.g2w

H.2. Équations de l'hyperbole

À partir du grand axe A’A = 2a et de la distance des foyers FF’ = 2c on définit le nombre positif b tel que b² = c² – a².

L'hyperbole a pour équation x²/a² – y²/b² = 1.

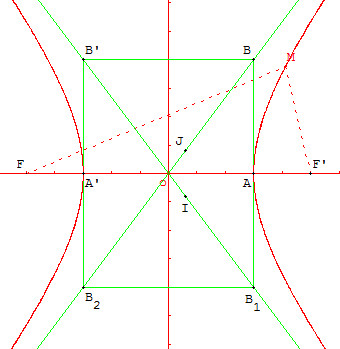
Avec GéoPlan on définit les deux fonctions

f1 fonction: x|->b*rac(x^2/a^2-1)
f2 fonction: x|->-b*rac(x^2/a^2-1)

Télécharger la figure GéoPlan hyperbole2.g2w

Équation de l'hyperbole par rapport à ses asymptotes

Les points B(a, b) et B’(– a, b) sont situés sur les asymptotes.
Dans le repère (o, oI, oJ) formé par les deux asymptotes, l'hyperbole a pour équation :
y = .

Avec GéoPlan

 f fonction: x|->c^2/(4x)
  h graphe de f sur [-20,20] (1000 points, repère R)
  Objet dessinable h, particularités: rouge, points liés

  Technique GéoPlan : le point M reste sur l'hyperbole grâce à la méthode du point collé sur le graphe de f.

Télécharger la figure GéoPlan hyperbole3.g2w

Cercle directeur d'une conique à centre

Étant donné deux points F et O et un cercle (c) de centre O et de rayon 2a, l'ensemble des centres des cercles tangents à (c) et passant par F est une conique à centres de foyer F et O. (c) est le cercle directeur de la conique.

Pour un point M du cercle, la médiatrice (m) de [FM] est tangente à la conique, en N, centre du cercle variable, situé sur le rayon [OM].

Coniques comme enveloppes

Soit un point F et un cercle (c) étant considérés comme fixes,
un point M variable sur (c) et (m) la médiatrice de [FM].

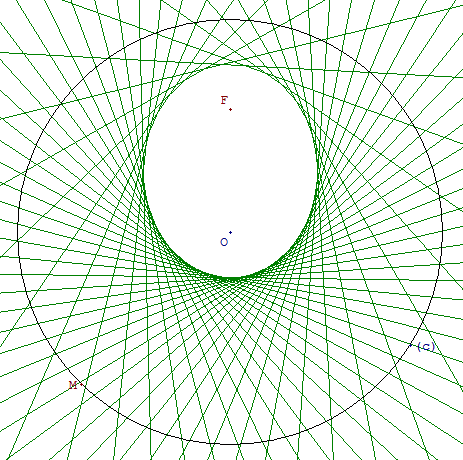
En répétant les constructions lorsque le point M varie sur le cercle (c), on voit apparaître l'enveloppe de la famille des médiatrices (m) ; courbe non tracée déterminée par ses tangentes.

Les courbes sont des coniques de foyers F et O le centre du cercle.
(c) est le cercle directeur de la conique.

Ellipse

Lorsque F est à l'intérieur du cercle, on obtient une ellipse.

Le mode trace de GéoPlan permet de mémoriser le tracé des tangentes.

Télécharger la figure GéoPlan envelop.g2w

Hyperbole

Lorsque F est à l'extérieur du cercle, on obtient une hyperbole.

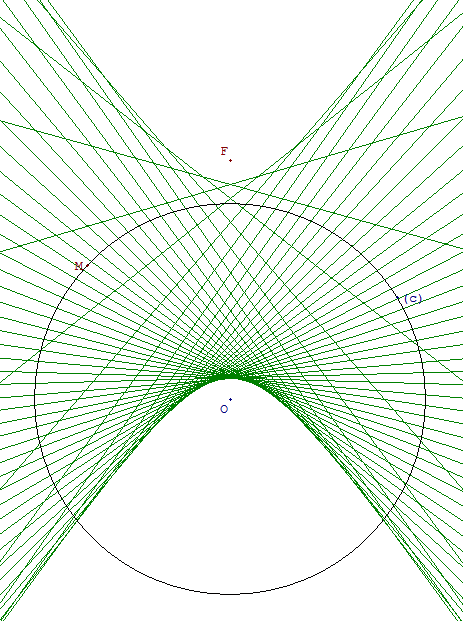
Si au lieu d'un cercle (c), on avait une droite (d), la courbe obtenue serait une parabole.

Construction par pliage

Sur une feuille, tracer un point F et un cercle (c). Amener par pliage le point F sur le cercle (c), marquer le pli et déplier.
En répétant un grand nombre de fois, en variant la position sur (c), on obtient la conique.