Descartes et les Mathématiques

Newton (1643-1727)

Un grand mathématicien du moyen-âge

Isaac Newton

Il est surtout reconnu pour avoir fondé la mécanique classique, pour sa théorie de la
gravitation universelle et la création, en concurrence avec Leibniz, du calcul infinitésimal.

En optique, il a développé une théorie de la couleur basée sur l'observation selon
laquelle un prisme décompose la lumière blanche en un spectre visible.

Il a aussi inventé le télescope à réflexion composé d'un miroir primaire concave
appelé télescope de Newton.

Sommaire

1. Isaac Newton

2. Le problème de Pappus

3. Ellipse tangente à 5 droites

3.1. Construction du centre de l'ellipse

3.2. Construction du point de contact avec [BC]

3.5. Ellipse passant par cinq points

4. Newton dans ce site

5. Principes mathématiques de la philosophie naturelle

2. Le problème de Pappus

Newton démontra le problème à quatre droites de Pappus, que Descartes avait déjà étudié.

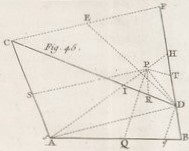
Newton précise que sa solution ne consiste pas en un calcul analytique,
mais une démonstration géométrique, telle que l'exigeait les Anciens.

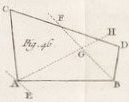
3. Conique tangente à cinq droites

...

3.1. Construction du centre de l'ellipse

Les tangentes ABG, BCF, GCD, FDE et EA sont données.

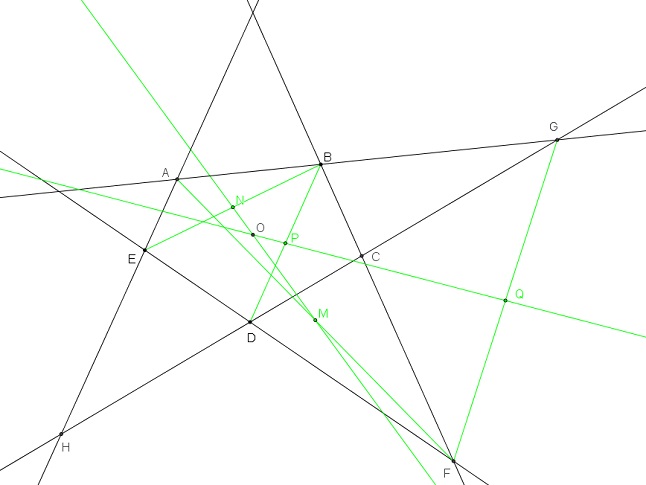
M et N sont les milieux des diagonales [AF] et [BE] du quadrilatère ABFE,
formé par quatre des tangentes.
La droite (MN) menée par les milieux passe par le centre de l'ellipse.

P et Q sont les milieux des diagonales [BD] et [GF] du quadrilatère croisé BGDF,
formé par quatre autres des cinq même tangentes
La droite (PQ) des milieux passera encore par le centre de l'ellipse.

Ainsi O est le point d'intersection de (MN) et (PQ).

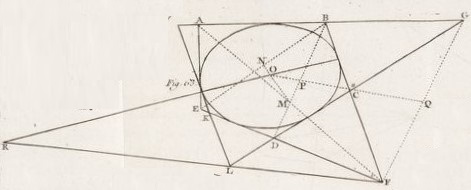
Figure de Newton

3.2. Construction du point de contact B₁ avec [BC]

Tirer ensuite (KL), symétrique de la tangente (BC) par rapport à O,
donc (KL), parallèle à (BC),est une tangente à la conique.

L et K sont les points où cette nouvelle tangente coupe les tangentes DCG et EDF.

C, K et F, L sont les points où les tangentes parallèles rencontrent
les tangentes non parallèles (CK) et (FL).
Les droites (CK) et (FL) se coupent en R.
Par le centre O, la droite (RO) coupe les deux tangentes (CF) et (KL)
en B₁ et B₂, points de la conique.

3.3. Construction du point de contact A₁ avec [AB]

Par la même méthode, par rapport à O, tracer la tangente symétrique à (AB).
L₁ et K₁ sont les points où cette nouvelle tangente coupe les tangentes non parallèles (BC) et (CD).
Les droites (BK₁) et (GL₁) se coupent en R₁.
La droite (R₁O) coupe les deux tangentes parallèles (AB) et (K₁L₁) en A₁ et A₂,
deux autres points de la conique.

3.4. Construction du point de contact C₁ avec [CD]

De même, tracer la tangente symétrique à (CD) par rapport au centre O..
L₂ et K₂ sont les points où cette nouvelle tangente coupe les tangentes non parallèles (BC) et (AE).
Les droites (CK₂) et (HL₂) se coupent en R₂.
La droite (R₂O) coupe les deux tangentes parallèles (CD) et (K₂L₂) en C₁ et C₂,
deux autres points de la conique.

3.5. Ellipse passant par cinq points

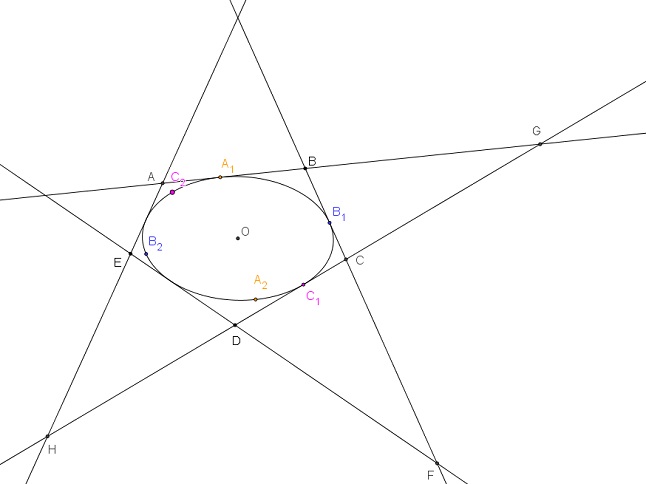
Les trois points de contact A₁, B₁, C₁ et deux autres points A₂, B₂ déterminent cinq points
de la conique solution, tangente aux cinq droites.

Figure dans GeoGebraTube : Ellipse de Newton tangente à 5 droites

4. Newton dans ce site

Droite de Newton d'un triangle.

Relation de Newton pour une division harmonique :
[A, B, C, D] = −1 si et seulement si IA² = IB² = . où I est le milieu de [AB].

Trident de Newton (ou parabole de Descartes)
La solution du problème de Pappus à cinq droites, où quatre droites sont parallèles
et la cinquième perpendiculaire aux autres est une cubique, que Newton a nommé trident.

5. Œuvre de Newton

Philosophiae naturalis principia ... - gallica.bnf.fr [latin]

Principes mathématiques de la philosophie naturelle [traduit du latin]

Table des matières

Mobile friendly

Dans d'autres pages du site

Index histoire des mathématiques

La Géométrie de Descartes

Page n^o 209, créée le 31/7/2018