Descartes et les Mathématiques

Le plan projectif

Théorémes de Desargues, de Pappus. Division harmonique ; trapèze et quadrilatère complets ;
droite de Newton et point de Miquel.

Sommaire

1. Configuration du trapèze complet

2. Pappus

3. Desargues

4. a. Division harmonique

    b. Quadrilatère complet

Géométrie euclidienne

    2.1. Droite de Newton

    2.2. Droites des milieux

    2.3. Point de Miquel - Cercle de Miquel

    2.4. Alignement des orthocentres

    2.5. Droite de Newton d'un triangle

Définitions

Girard Desargues (Français 1591-1661) est le créateur de la géométrie projective, étude de propriétés qui se conservent par projection centrale : alignement, point de concours, contact et birapport.

Intuitivement la droite projective est une droite affine complétée par un point, appelé point à l'infini. Elle est en bijection avec R ∪ {∞}
(ne pas confondre le complété projectif R ∪ {∞} avec R ∪ {– ∞, + ∞}).

Le plan projectif est un plan affine complété par la droite de l'infini, réunion des points à l'infini des droites de ce plan.
Dans le plan projectif, deux droites parallèles ont en commun un point à l'infini (point de fuite sur la ligne d'horizon en perspective).
De cette façon, deux droites distinctes du plan projectif ont toujours un point commun.

Le plan projectif est associé au groupe des transformations projectives qui conservent alignement, concours, division harmonique et birapport.

Une des catastrophes de l'enseignement français des mathématiques est que ces notions difficiles, mais essentielles en dessin, imagerie et physique, ne sont plus enseignées au lycée depuis 1970.

Nous donnons ici quelques exemples d'alignements et de point de concours.

1. Configuration du trapèze complet

Définition du trapèze complet

Définition : Un trapèze complet est un quadrilatère complet dont un des sommets est un point à l'infini

Un trapèze complet (qui n'est pas un parallélogramme) est formé de quatre droites du plan, deux droites parallèles et deux sécantes coupant les parallèles en quatre points.
Le trapèze complet (strict) a quatre côtés, cinq sommets (les quatre sommets du trapèze et le point d'intersection des côtés non parallèles), deux diagonales et un point diagonal.

Remarque : un trapèze est un quadrilatère, possédant au moins deux côtés opposés parallèles.
Un parallélogramme est un cas particulier de trapèze.
Un parallélogramme est un trapèze complet dont deux des sommets sont des points à l'infini.

Théorème du trapèze

Dans un trapèze, la droite joignant le point d'intersection des côtés non parallèles au point d'intersection des diagonales, passe par les milieux des côtés parallèles.

Activité

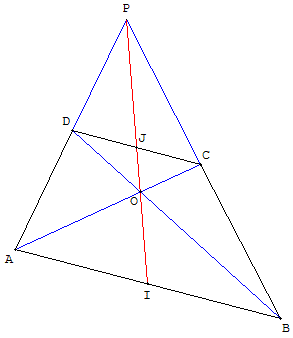
A, B et C sont trois points du plan ; D est un point sur la parallèle à (AB) passant par C.

ABCD est un trapèze de bases [AB] et [CD] ayant pour milieux I et J. Les diagonales [AC] et [BD] se coupent en O. Les droites (BC) et (AD) se coupent en P.

Montrer que les points I, J, O et P sont alignés.

Démonstration avec l'homothétie

Utiliser les propriétés des homothéties transformant le segment [AB] en [CD].

Réciproque : CDP est un triangle, J le milieu de [CD], O un point de la droite (PJ) distinct de P, de J et du symétrique de J par rapport à P.
(CO) coupe (PD) en A et (DO) coupe (PC) en B.

Montrer que les droites (AB) et (CD) sont parallèles et que le point I, intersection de (AB) et (PJ), est le milieu de [AB].

Figure interactive dans GeoGebraTube : trapèze complet

Démonstration avec des barycentres

Il existe un nombre k différent de 0, 1 et -1 tel que le vecteur = − k , soit 2 + 2k = .
O est le barycentre de (P, 2k) et (J, 2).
Comme J est milieu de [CD], la forme vectorielle du théorème de la médiane dans le triangle OCD permet d'écrire :
+ = 2 donc + + 2k = (formule 1) ;
O est le barycentre de (P, 2k) ; (C, 1) et (D, 1).

D'après la règle d'associativité des barycentres, on trouve que l'intersection A de (PD) avec (CO) est le barycentre partiel de (P, 2k) et (D, 1) et aussi que B est le barycentre partiel de (P, 2k) et (C, 1) ;
donc 2k + = et 2k + = (formules 2 et 3).

En calculant à partir de P, dans les formules 2 et 3, on trouve (2k + 1) = et (2k + 1) = ,
d'où en faisant la différence de ces deux égalités on trouve (2k + 1) = . Ces deux derniers vecteurs sont colinéaires et (AB) // (CD).

De même, en calculant à partir de D, dans la formule 2, on trouve (2k + 1) + 2k = ;

D est le barycentre de (A, 2k + 1) et (P, – 2k).

La formule vectorielle de Leibniz (α + β) = α + β , en plaçant M en O, permet d'écrire = (2k + 1) – 2k
et en remplaçant dans la formule 1 on obtient : + (2k + 1) = : O est le barycentre de (C, 1) et (A, 2k + 1).

Des calculs similaires avec la formule 3, à partir du point C, permettent d'écrire (2k + 1) + 2k = ;
C est le barycentre de (B, 2k + 1) et (P, – 2k) : + (2k + 1) = : O est le barycentre de (D, 1) et (B, 2k + 1).

En remplaçant ces deux derniers résultats dans la formule 1, on trouve – (2k + 1) – (2k + 1) + 2k = ;
O est le barycentre de (A, 2k + 1) ; (B, 2k + 1) et (P, – 2k).
D'après la règle d'associativité des barycentres, on trouve que le point d'intersection I de (PO) avec (AB) est le barycentre partiel de (A, 2k + 1) et (B, 2k + 1).

Les deux coefficients étant égaux, I est le milieu de [AB].

2. Pappus

Pappus d'Alexandrie (vers l'an 300)

Théorème de Pappus

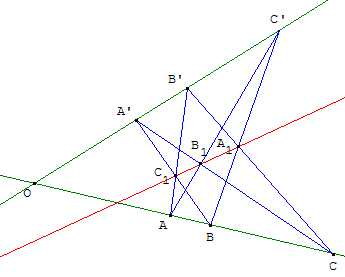
Soit (d) et (d’) deux droites du plan projectif ayant le point O comme intersection ; A, B et C trois points de (d) distincts de O ; A’, B’ et C’ trois points de (d’) distincts de O.

Les points d'intersection A₁, B₁ et C₁ sont alignés (voir figure).

Remarque : on trouve diverses formes de ce théorème en géométrie affine en tenant compte que deux droites du plan projectif, toujours concourantes, correspondent à deux droites sécantes ou parallèles du plan affine.

En géométrie affine, voir le cas particulier où (AB’)//(A’B). (la droite (A₁B₁) est alors la droite de l'infini.)

D'après le théorème de Pascal, pour un hexagone inscrit dans une conique, les points d'intersection des côtés opposés de l'hexagone, s'ils existent, sont alignés.

Les deux droites (d) et (d’) peuvent être considérées comme une conique dégénérée : pour l'hexagramme AB’CA’BC’, le théorème de Pappus-Pascal affirme l'alignement des points A₁, B₁ et C₁.

Parallélogramme de Pappus : preuve par homothétie

Petit théorème de Pappus

Démonstration par Pappus du théorème de Pythagore

Le problème de Pappus

3. Desargues

Droites concourantes en O

Desargues Girard - Géomètre lyonnais 1591-1661

Théorème de Desargues (forme forte)

Perspective de deux triangles

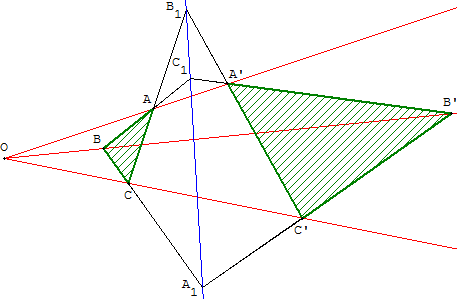
Soit ABC et A’B’C’ deux triangles (distincts d'un espace projectif) ayant leurs sommets deux à deux distincts.

Si les droites (AA’), (BB’) et (CC’) sont concourantes, alors les points de concours A₁, B₁ et C₁ sont alignés.

Le point O est le pôle de la perspective (ou centre d'homologie) ;

archaically en : perspector

(A₁, B₁) est l'axe de la perspective (ligne de terre ou axe d'homologie) ;

archaically en : perspectrix

Télécharger la figure GéoPlan desargues.g2w

Apllications :

Axe orthique

Droite de Gergonne

Réciproque, voir :
    – joindre deux points d'une droite avec une règle trop courte ;
    – le point de concours de deux droites étant situé hors de la feuille, construire une droite passant par cette intersection inaccessible.

Droites parallèles

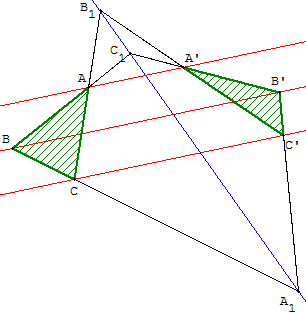
Cas particulier où le centre O est le point à l'infini sur la droite (AA’).

Soit ABC et A’B’C’ deux triangles, ayant leurs sommets deux à deux distincts, tels que (AA’) // (BB’).

Les droites (AA’) et (CC’) sont parallèles, si et seulement si les points A₁, B₁ et C₁ sont alignés.

Télécharger la figure GéoPlan desargues_para.g2w

Démonstration historique « par le relief »

Démonstration avec une perspective de centre O, à la façon de Desargues (1637)

Figure dessinée dans le plan, que l'«on voit » comme la représentation en perspective d'une figure de l'espace

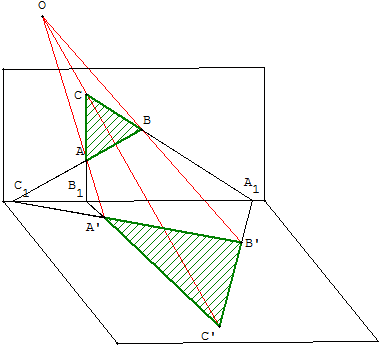
A’B’C’ dans le « plan horizontal »,
ABC dessiné dans un « plan vertical »,
l'œil du peintre étant situé au pôle O.

L'axe de la perspective est alors la droite d'intersection des deux plans.

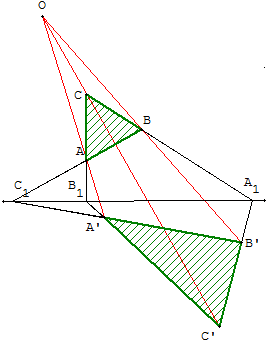
Même figure dépouillée des plans permettant de « voir » dans l'espace

Télécharger la figure GéoPlan thm_desargues.g2w

Commande GéoPlan
Taper P pour effacer/afficher les Plans permettant que l'«on voit » les triangles comme la représentation en perspective d'une figure de l'espace.

Visualisation d'une pyramide de sommet O et de base A’B’C’ coupée par le plan (ABC).

Desargues transgresse une des règles d'Euclide qui est de démontrer une propriété de géométrie plane dans le seul cadre de la géométrie plane.

Il peut être considéré comme l'inventeur de la méthode des transformations permettant des démonstrations par transfert de propriété.

Il utilise l'espace pour la visualisation d'un problème plan :

Imaginons que la figure ci-dessus soit une représentation de l'espace :

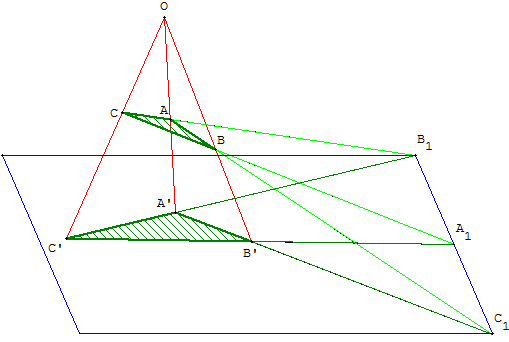
Le triangle ABC est l'image en perspective du triangle A’B’C’.
Les points A₁, B₁ et C₁ sont alignés sur la ligne de terre, droite d'intersection des plans (ABC) et (A’B’C’). On appelle aussi axe d'homologie cette ligne de terre.

Théorème de Desargues dans l'espace

Ces figures s'appliquent, dans l'espace, à deux triangles non coplanaires.
Pour deux triangles coplanaires, on utilise une figure en perspective.

Télécharger la figure GéoPlan desargues_pyramide.g2w

Géométrie affine

Forme forte du théorème de Desargues

Si le point C₁ est le point à l'infini, les droites (AB) et (A’B’) sont parallèles, et sont parallèles à (A₁B₁).

Remarque : des droites concourantes dans un espace projectif correspondent à des droites sécantes ou parallèles dans un espace affine.

En géométrie affine, on trouvera plusieurs énoncés du théorème de Desargues tenant compte de ce fait, comme ce cas particulier où les triangles ont deux côtés distincts parallèles.
– La droite (A₁B₁) est alors la droite de l'infini.

Ce qui donne, dans le plan affine, la forme faible du théorème de Desargues

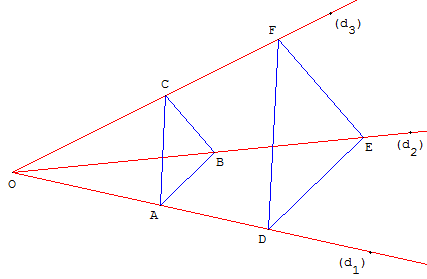
Soient (d₁), (d₂) et (d₃) trois droites distinctes concourantes ou parallèles et soient ABC et A’B’C’ deux triangles non plats tels que A et A’ soient sur (d₁) ; B et B’ sur (d₂) ; C et C’ sur (d₃).
Si (AB)//(A’B’) et (BC)//(B’C’) alors (AC)//(A’C’).

Télécharger la figure GéoPlan desargues.g2w

Réciproque

Soient ABC et A’B’C’ deux triangles non plats, tels que (AB)//(A’B’), (BC)//(B’C’) et (AC)//(A’C’), alors les droites (AA’), (BB’) et (CC’) sont concourantes ou parallèles.

Autrement dit, deux triangles ayant leurs côtés deux à deux parallèles, sont homothétiques ou translatés l'un de l'autre.

Calcul barycentrique

Dans le Bulletin APMEP n^o 493 mars-avril 2011, Michel Fréchet propose une démonstration élégante et surprenante de ce théorème avec une figure de l'espace.
Il rappelle un exercice de géométrie plane, fastidieux et non convainquant, figurant dans des livres de terminale S, ayant pour objectif de démontrer ce théorème par le calcul :

  – Soit α, β et γ les coordonnées barycentriques de O respectivement par rapport aux couples de points (A, A’) ; (B, B’) et (C, C’).
On a : α + (1 – α) = ; β + (1 – β) = et γ + (1 – γ) = .
Les points A₁, B₁ et C₁ existent si les côtés des triangles ABC et A’B’C’ ne sont pas deux à deux parallèles. Les coefficients α, β et γ sont alors deux à deux distincts.

  – Parachutons le point K, barycentre des points pondérés (A, α) et (B, – β).
Pour ce point K appartenant à la droite (AB), la fonction vectorielle de Leibniz permet d'écrire α – β = (α – β) .
En utilisant les coordonnées barycentriques ci-dessus, on a (α – 1) – (β – 1) = [(α – 1) – (β – 1)] . K est donc le barycentre des points pondérés [A’, (α – 1)] et [B’, – (β – 1)] et appartient à la droite (A’B’).
Le point K, situé à l'intersection de (AB) et (A’B’), n'est autre que le point C₁. On a donc :
C₁ est le barycentre des points pondérés (A, α) et (B, – β) ; soit α – β = (α – β) .
De même B₁ est le barycentre des points pondérés (C, γ) et (A, – α) ; soit γ – α = (γ – α) ,
et A₁ est le barycentre des points pondérés (B, β) et (C, – γ) ; soit β – γ = (β – γ) .

  – En additionnant, membre à membre, ces trois dernières égalités on a :
(β – γ) + (γ – α) + (α – β) = β – γ + γ – α + α – β = .
Les trois réels (β – γ), (γ – α) et (γ – α), n'étant pas nuls, les points A₁, B₁ et C₁ sont alignés (C₁ pouvant être considéré comme un barycentre de A₁ et B₁).

4. a. Division harmonique

Définitions : quatre points distincts alignés A, B, C, D sont en division harmonique si et seulement si on a l'une des quatre relations équivalentes :
définition : = − ;

relation de Descartes : ;

relation de Newton : IA² = IB² = . où I est le milieu de [AB] ;

relation de Mac-Laurin : . = . où J est le milieu de [CD].

Birapport de quatre points alignés : c'est le nombre , noté [A, B, C, D].

La notion de birapport (ou rapport anharmonique) remonte à Pappus d'Alexandrie.

Si quatre points alignés A, B, C, D forment une division harmonique, le birapport est égal à –1 et on note [A, B, C, D] = −1 ;
Les points C et D sont conjugués harmoniques par rapport aux point A et B.

Sur une droite (AB), le point à l'infini est le conjugué harmonique du milieu de [AB] par rapport à A et B. Réciproquement, le milieu est le conjugué du point à l'infini.

Voir : polaire d'un point par rapport à une droite ou à un cercle

WikiPédia : division harmonique

4.b. Quadrilatère complet

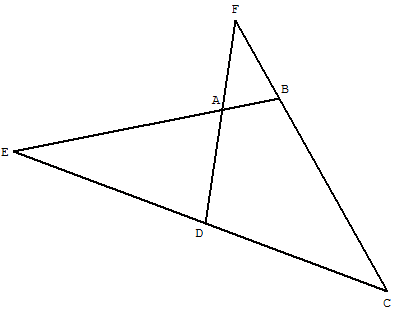
Définition : un quadrilatère complet est formé de quatre droites du plan se coupant, deux à deux, en six points.

Remarques : deux des points peuvent être « à l'infini ». Le quadrilatère est alors un parallélogramme. L'étude de ce cas particulier ne présente pas d'intérêt dans le plan projectif.
Si uniquement un des points est à l'infini, on obtient un trapèze complet.

Dans la suite de cet article nous considérons le quadrilatère complet strict où deux quelconques des quatre droites ne sont pas parallèles, trois quelconques ne sont concourantes :

A, B, C et D sont quatre points du plan formant un quadrilatère convexe (qui n'est pas un trapèze), les droites (AB) et (CD) se coupent en E, puis (AD) et (BC) en F.

Les quatre droites (AB), (AD), (CB) et (CD) déterminent un quadrilatère complet ayant les six sommets A, B, C, D, E et F.

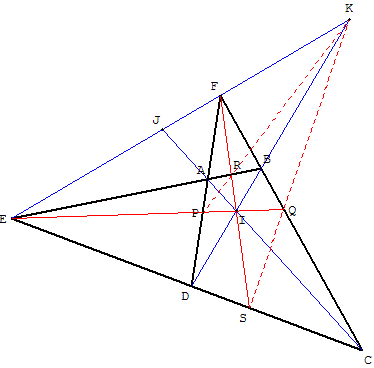
Les trois droites (AC), (BD) et (EF) sont les diagonales du quadrilatère complet, leurs points d'intersection I, J, K sont les points diagonaux.

Le quadrilatère complet est à distinguer du quadrangle complet qui a quatre sommets, six côtés et trois points diagonaux.

Dans un espace projectif, le dual d'un quadrilatère complet est un quadrangle et réciproquement.

Figure interactive dans GeoGebraTube : quadrilatère complet

       Feuille de travail dynamique avec GeoGebra

Diagonales et divisions harmoniques dans un quadrilatère complet

WikiPédia : Quadrilatère complet
dupliqué dans FrWiki : Quadrilatère complet

2. Géométrie euclidienne

2.1. Droite de Newton d'un quadrilatère complet

Dans la suite de ces paragraphes, les quatre droites (AB), (AD), (CB) et (CD) déterminent un quadrilatère complet de sommets A, B, C, D, E et F.
[AC], [BD] et [EF] sont les diagonales du quadrilatère complet.

Les milieux I, J et K des diagonales sont alignés (Théorème de Newton).

La droite qui porte les points I, J, K est dite droite de Newton du quadrilatère complet.

Télécharger la figure GéoPlan qua_com1.g2w

Démonstration

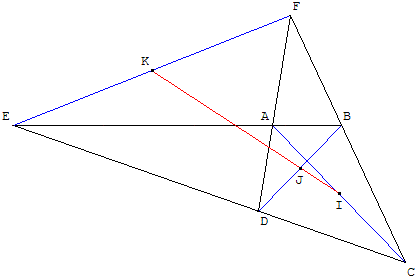
Soit G et H les points définis par = et = .

Soit h₁ l'homothétie de centre F qui transforme B en C, et h₂ l'homothétie de centre F qui transforme D en A.

h₃ = h₂ o h₁ et h₄ = h₁ o h₂

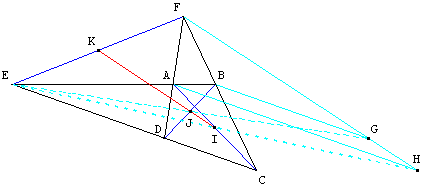
L'image de (BG) par h₁ est (DC), l'image de (DC) par h₂ est (AH), donc l'image de (BG) par h₃ est (AH). De même, l'image de (DG) par h₄ est (CH).

La composition des homothéties de même centre est commutative : h₃ = h₄ est une homothétie de centre F. D'où l'image de G par h₃ est H ; les points F, G et H sont alignés.

Comme = , EDGB est un parallélogramme de centre J ; EJ = EG.

= , ECHA est un parallélogramme de centre I ; EI = EH.

L'homothétie de centre E et de rapport transforme F en K, G en J, H en I.

Comme les points F, G, H sont alignés; les transformés I, J, K sont donc alignés.

Télécharger la figure GéoPlan qua_com9.g2w

2.2. Droites des milieux d'un quadrilatère complet

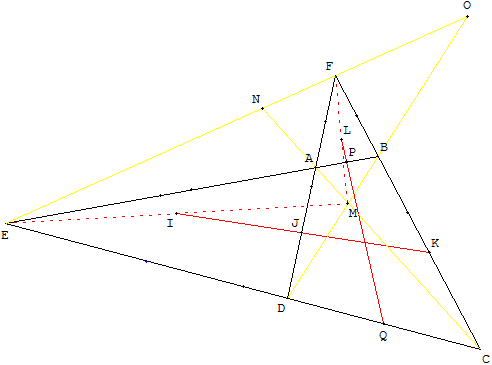
Les milieux I de [ME], J de [AD] et K de [BC] sont alignés.
De même, les milieux L de [MF], P de [AB] et Q de [CD] sont aussi alignés.

Les diagonales [AC] et [BD] du quadrilatère complet se coupent en M :
  • Les milieux I de [ME], J de [AD] et K de [BC] sont alignés.
  • De même, les milieux L de [MF], P de [AB] et Q de [CD] sont aussi alignés.

De même, si les diagonales [AC] et [EF] se coupent en N, on trouve que :
  • Les milieux de [NB], de [AF] et de [CE] sont alignés ;
  • ainsi que les milieux de [ND], de [AE] et de [CF].

Enfin, si les diagonales [BD] et [EF] se coupent en O :
  • Les milieux de [OA], de [BF] et de [DE] sont alignés ;
  • ainsi que les milieux de [OC], de [BE] et de [DF] sont alignés.

Télécharger la figure GéoPlan qua_com3.g2w

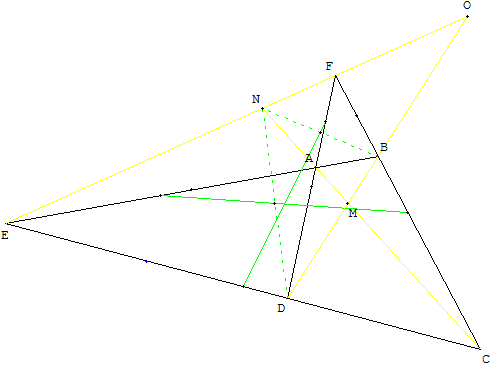
Les milieux de [NB], de [AF] et de [CE] sont alignés ;
ainsi que les milieux de [ND], de [AE] et de [CF].

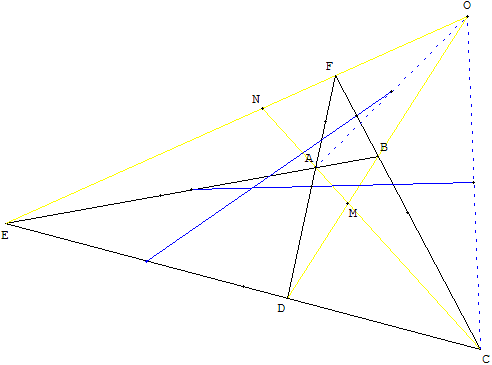
Les milieux de [OA], de [BF] et de [DE] sont alignés ;
ainsi que les milieux de [OC], de [BE] et de [DF].

2.3. Point et cercle de Miquel

Point de Miquel d'un quadrilatère complet ou d'un triangle

Point de Miquel d'un quadrilatère complet

Théorème du quadrilatère complet

Les quatre cercles circonscrits aux triangles ADE, BCE, ABF et CDF, formés par les sommets pris trois à trois, sont concourants en M, point de Miquel du quadrilatère complet.

Point de Miquel d'un triangle associé à une transversale

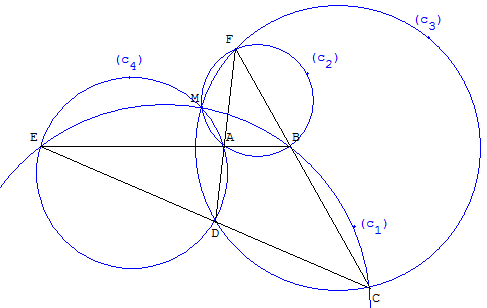
Étant donné un triangle FDC et une transversale (d), ne passant par les sommets, coupant les côtés (FD) en A, (FC) en B et (DC) en E. Les trois cercles ADE, BCE et ABF sont sécants en un point M, point de Miquel du triangle FDC associé à la transversale (d).

Le cercle circonscrit au triangle FDC passe par le point de Miquel.

Les démonstrations se font en utilisant les angles inscrits.

Figure interactive dans GeoGebraTube : point de Miquel

Autres concours de cercle, démontrés par Miquel, voir : triangles de Napoléon

Cercle de Miquel

Théorème des quatre cercles

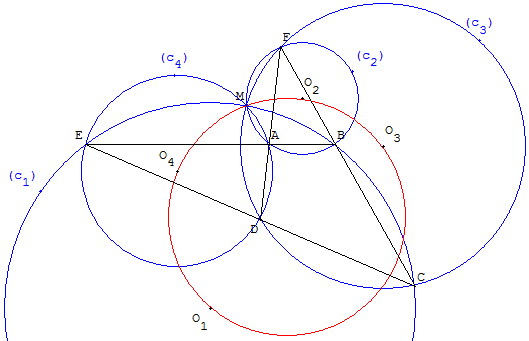
Les centres O₁, O₂, O₃, O₄ des quatre cercles et le point de Miquel M sont cocycliques ou alignés.

Le cercle contenant ces cinq points est dit cercle de Miquel.

Figure interactive dans GeoGebraTube : cercles de Miquel

Feuille de travail dynamique avec GeoGebra : point et cercle de Miquel

Figures exportées dans WikiPédia : théorème de Miquel

2.4. Alignement des orthocentres d'un quadrilatère complet

Les quatre triangles ABF, ADE, BCE et CDF formés par les côtés du quadrilatère complet pris trois à trois ont leurs orthocentres alignés sur la droite de Miquel, droite orthogonale à la droite de Newton, qui passe par les milieux des diagonales.

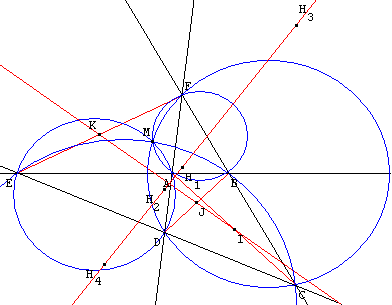
Télécharger la figure GéoPlan qua_com4.g2w

Démonstration avec un axe radical : géométrie du cercle

2.5. Droite de Newton d'un triangle

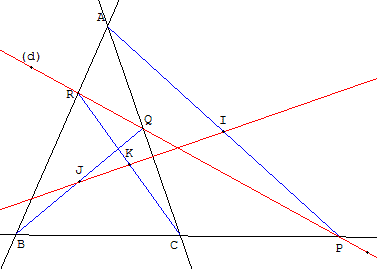
Rappel : Dans un triangle, une ménélienne est une droite ne passant pas par un des sommets.

Dans un triangle ABC, une ménélienne rencontre les côtés (BC), (CA) et (AB) respectivement aux points P, Q et R, distincts des sommets.
Soit I, J et K les milieux respectifs des segments [AP], [BQ] et [CR].

Alors les points I, J et K sont alignés sur la droite de Newton du triangle ABC, associée à la transversale (d).

Les quatre droites (AB), (AC), (PC) et (PQ), définissent un quadrilatère complet, admettant pour sommets les six points A, B, C, P, Q et R.

Les points I, J et K sont alignés sur la droite de Newton de ce quadrilatère complet.

Figure ci-dessus

La ménélienne rencontre deux côtés du triangle ABC.

Figure ci-dessous

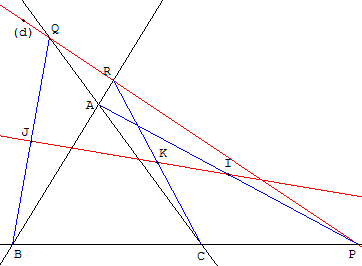
La ménélienne ne rencontre aucun des côtés du triangle.

Figure interactive dans GeoGebraTube : droite de Newton d'un triangle

     Feuille de travail dynamique avec GeoGebra

Article exporté dans WikiPédia : droite de Newton

Bibliographie

Jean-Louis Ayme - Une quarantaine de démonstrations concernant la droite de Newton : méthodes et techniques en géométrie - Ellipses - 2003
 Brigitte Sénéchal-Rozoy - Géométrie classique et mathématiques modernes - Hermann 1979
Angles et rotations - brochure IREM - Bordeaux 1996

Table des matières

Dans d'autres pages du site

Index 1^ère S

Épreuve pratique de terminale S

Google friendly

Téléchargement

Télécharger plan_projectif.doc : ce document au format « .doc ».
Google considère l'URL de ce document comme une erreur de type "soft 404"

Télécharger plan_projectif.pdf : ce document au format « .pdf »

Page n^o 46, réalisée le 21/6/2003
modifiée le 20/6/2012