 Descartes et les Mathématiques
Descartes et les Mathématiques
Les problèmes du BOA
Construction de triangles autour d'un triangle BOA - Triangles de Napoléon - Point de Torricelli.
SommaireA. Triangles isocèles - Rotation d'un triangle Partie B : triangles rectangles isocèles 1. Deux triangles rectangles isocèles 3. Deux autres triangles rectangles isocèles 4. Que de triangles rectangles isocèles ! 5. La médiane de l'un est la hauteur de l'autre 6. Trois triangles rectangles isocèles 7. Quatre triangles rectangles isocèles autour d'un quadrilatère |
Partie C : triangles équilatéraux 1. Quatre triangles équilatéraux 2. Trois triangles isocèles d'angles de 30° Quatre autres triangles équilatéraux 3. Trois triangles équilatéraux 4. Quatre triangles équilatéraux autour d'un quadrilatère 5. Deux triangles équilatéraux autour d'un carré D. BOA isocèle E: Carrés autour d'un triangle BOA |
Voici quelques configurations pouvant facilement s'étudier de diverses manières : autrefois avec les transformations (rotations - homothéties), le produit scalaire en première S ou les complexes en terminale S.
A. Triangles isocèles
Rotation d'un triangle
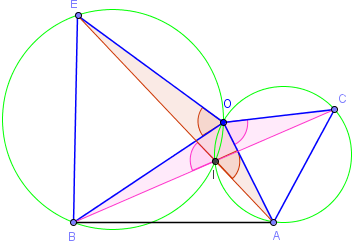
Soit deux triangles isocèles semblables, OAC et OBE, à l'extérieur d'un triangle BOA :
OAC est un triangle isocèle en O, d'angle AOC = α,
OBE est un triangle isocèle en O, semblable à OAC, également d'angle BOE = α.
Les droites (AE) et (BC) sont concourantes en I.
Conclusions
Les triangles OAE et OCB sont isométriques ;
AE = BC ;
l'angle des droites (AE) et (BC) est égal à α ;
Les cercles circonscrits à OAC et OBE se recoupent en I.
Indications : rotation d'un triangle
Par la rotation de centre O et d'angle α, A a pour image C et E a pour image B, donc [AE] a pour image [CB].
Le triangle OAE a pour image OCB.
Comme la rotation est une isométrie, on a AE = BC et comme l'angle d'une droite et de sa transformée est égal à l'angle de la rotation, on a AIC = α.
Comme AIC = AOC = α, les points A, C, O et I sont cocycliques et le point I est sur le cercle circonscrit à OAC.
On a aussi EIB = EOB = α, et le point I est sur le cercle circonscrit à OBE.
I est le deuxième point d'intersection des deux cercles circonscrits.
![]() Figure interactive dans GeoGebraTube : deux triangles à l'extérieur d'un triangle
Figure interactive dans GeoGebraTube : deux triangles à l'extérieur d'un triangle
Voir deux cas particuliers :
– ci-dessous ; deux triangles rectangles isocèles OAC et OBE autour de BOA,
– deux triangles équilatéraux OAC et OBE autour de BOA.
Partie B. Triangles rectangles isocèles
B.1. Deux triangles rectangles isocèles

Construction de deux triangles rectangles isocèles, en O, autour d'un triangle BOA ; les deux angles droits en O.
BOA est un triangle quelconque tel que (![]() ,
, ![]() ) = α (α ∈ ]0, π[),
) = α (α ∈ ]0, π[),
OAC et OEB sont deux triangles rectangles isocèles directs.
Montrer que les droites (AE) et (BC) sont perpendiculaires et que AE = BC.
• Utilisation d'une rotation de centre O et d'angle ![]() .
.
A a pour image C et E a pour image B, donc [AE] a pour image [CB].
Le triangle OAE a pour image OCB.
D'après les propriétés de la rotation on a AE = CB, et comme l'angle d'une droite et de sa transformée est égal à l'angle de la rotation, on a (AE) ⊥ (BC).
• Utilisation du produit scalaire
![]() =
= ![]() −
− ![]() : CB2 = OB2 + OC2 −
2
: CB2 = OB2 + OC2 −
2 ![]() .
.![]() ,
,
![]() =
= ![]() −
− ![]() : EA2 = OA2 + OE2 − 2
: EA2 = OA2 + OE2 − 2 ![]() .
.![]() .
.
On a OA = OC et OB = OE et si α = (![]() ,
,
![]() ) l'expression des deux produits scalaires avec normes et angle donne :
) l'expression des deux produits scalaires avec normes et angle donne :
![]() .
.![]() =
= ![]() .
. ![]() = OB × OA × cos (α +
= OB × OA × cos (α + ![]() ).
).
Les deux produits scalaires sont égaux et CB2 = EA2 d'où les longueurs CB et EA sont égales.
Pour l'orthogonalité, calculons un autre produit scalaire :
![]() .
. ![]() = (
= (![]() −
− ![]() )
. (
)
. (![]() −
− ![]() )
=
)
= ![]() .
. ![]() +
+ ![]() .
. ![]() (les deux dernières soustractions correspondent à des produits scalaires nuls de vecteurs orthogonaux).
(les deux dernières soustractions correspondent à des produits scalaires nuls de vecteurs orthogonaux).
![]() .
. ![]() = OB × OA × cos α + OC × OE × cos (− α + π) = 0, les angles étant supplémentaires, les cosinus sont opposés.
= OB × OA × cos α + OC × OE × cos (− α + π) = 0, les angles étant supplémentaires, les cosinus sont opposés.
Le produit scalaire est nul, ce qui démontre que les droites (AE) et (BC) sont perpendiculaires.
• Utilisation des complexes en TS : choisir un repère d'origine O.
Si A a pour affixe a et B pour affixe b, les points C et E ont pour affixe c = ia et e = −ib.
![]() a pour affixe e − a,
a pour affixe e − a, ![]() a pour affixe b − c = i (e − a) ; (b − c)/(e − a) = i.
a pour affixe b − c = i (e − a) ; (b − c)/(e − a) = i.
Le module 1, de ce quotient égal à i, démontre l'égalité des longueurs EA et CB. L'argument de i, égal à ![]() , permet de conclure à l'orthogonalité.
, permet de conclure à l'orthogonalité.
Remarques : si I est le milieu de [CE], (AB) est perpendiculaire à la médiane (CI) de OCE : voir médiane de l'un, hauteur de l'autre.
Voir aussi l'exploitation de deux carrés complétant les triangles rectangles isocèles dans la page carrés autour de BOA.
![]() Télécharger la figure GéoPlan tr_boa_1.g2w
Télécharger la figure GéoPlan tr_boa_1.g2w
B.2. Quadrilatère de Varignon
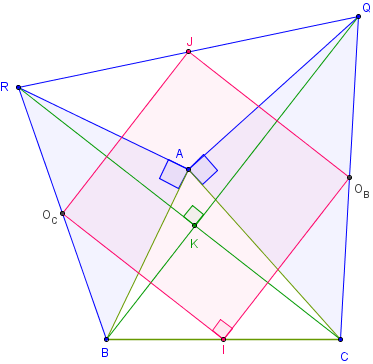
Étant donné un triangle ABC, complété par deux triangles ACQ et ABR rectangles isocèles, en A, et un quatrième triangle AQR, le quadrilatère de Varignon IOBJOC, qui joint les milieux des côtés extérieurs de la figure BCQR, est un carré.
I, OB, J et OC sont les milieux des côtés du quadrilatère BCQR.
Comme au paragraphe précédent, la rotation de centre A et d'angle ![]() transforme [RC] en [BQ.
transforme [RC] en [BQ.
Les deux diagonales [CR] et [BQ] sont donc de longueur égale et perpendiculaires.
Le quadrilatère BCQR est un pseudo-carré.
Le théorème de Varignon affirme que IOBJOC, est un parallélogramme dont les côtés sont parallèles aux diagonales du quadrilatère ABEC,
avec IOB = ![]() BQ et IOC =
BQ et IOC = ![]() CR.
CR.
Comme les deux diagonales du pseudo-carré sont égales et perpendiculaires, il en est de même pour celles du parallélogramme IOBJOC, ce qui permet d'assurer que c'est un carré.
![]() Figure interactive dans GeoGebraTube : quadrilatère de Varignon
Figure interactive dans GeoGebraTube : quadrilatère de Varignon
Remarque : voir aussi deux carrés, de centre D et F, complétant les triangles rectangles isocèles dans la page carrés autour de BOA.
B.2.b. BOA dégénéré

Les propriétés subsistent lorsque les points B, O et A sont alignés.
![]() Télécharger la figure GéoPlan tr_boa_9.g2w
Télécharger la figure GéoPlan tr_boa_9.g2w
B.3. Deux autres triangles rectangles isocèles

À l'extérieur d'un triangle BOA, tracer deux triangles rectangles isocèles, les angles droits en A et B, deux angles aigus de 45° en O.
BOA est un triangle quelconque, OAD et OFB sont deux triangles rectangles isocèles directs, respectivement en A et B.
Le point M est l'intersection des droites (BD) et (AF).
Montrer que la droite (OM) est orthogonale à (AB).
Autre formulation avec la construction de deux carrés OADC et OEFB, voir : deux carrés à l'extérieur de BOA
![]() Télécharger la figure GéoPlan tr_boa_8.g2w
Télécharger la figure GéoPlan tr_boa_8.g2w
Solution
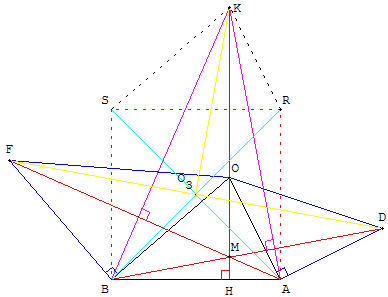
Soit BARS le carré de côté [BA], de centre O3, situé du même côté de (BA) que O.
La rotation de centre O3 et d'angle ![]() transforme B en A, A en R.
transforme B en A, A en R.
La rotation transforme D en un point K tel que KR = AD = OA et (KR), perpendiculaire à (AD), est parallèle à (OA) ;
AOKU est un parallélogramme,
donc OK = BA et (OK) est perpendiculaire à (AB).
Le point K est donc situé sur le prolongement de la perpendiculaire en O à (AB), à une distance égale à AB de O.
[BD] a pour image [AK] : (BD) et (AK) sont perpendiculaires et BD = AK.
On montre de même que ce point K est l'image de F par la rotation de centre O3 et d'angle − ![]() : (AF) et (BK) sont perpendiculaires et AF = BK.
: (AF) et (BK) sont perpendiculaires et AF = BK.
(BD), (AF) et (OK) sont les trois hauteurs du triangle BAK. Elles sont concourantes en M orthocentre de triangle. La hauteur (OM) est orthogonale à (AB).
Remarques : Le triangle SKR, translaté du triangle BOA, est isométrique à BOA.
FKD est un triangle rectangle isocèle en K.
B.4. Que de triangles rectangles isocèles !
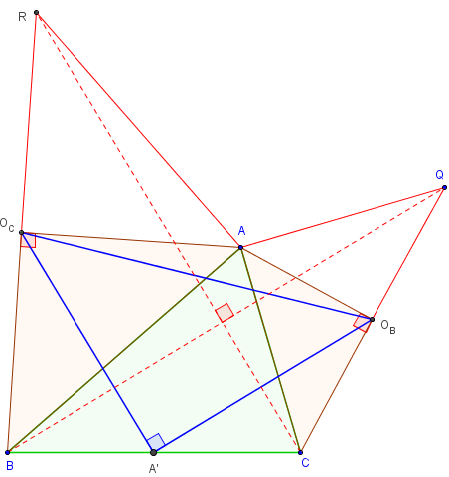
À l'extérieur d'un triangle, construire deux triangles rectangles isocèles dont les hypoténuses sont deux côtés du triangle.
OB et OC sont les sommets des demi-carrés construits à l'extérieur du triangle ABC.
Soit A' le milieu de [BC].
Montrer que A'OB = A'OC.
Un autre triangle rectangle isocèle
Construire le point R symétrique de B par rapport à OC, et le point Q symétrique de C par rapport à OB.
La rotation de centre A et d'angle ![]() transforme le triangle RAC en BAQ donc les segments [RC] et [BQ] sont perpendiculaires et de même longueur. Les droites des milieux A'OB et A'OC des triangles BCQ e CBR déterminent des segments perpendiculaires de même longueur égale à la moitié de RC ou BQ.
transforme le triangle RAC en BAQ donc les segments [RC] et [BQ] sont perpendiculaires et de même longueur. Les droites des milieux A'OB et A'OC des triangles BCQ e CBR déterminent des segments perpendiculaires de même longueur égale à la moitié de RC ou BQ.
De fait, A'OBOC est un triangle rectangle isocèle.
![]() Figure interactive dans GeoGebraTube : deux triangles rectangles isocèles autour d'un triangle
Figure interactive dans GeoGebraTube : deux triangles rectangles isocèles autour d'un triangle
Quadrilatère de Varignon
Avec deux triangles rectangles isocèles dont les sommets de l'angle droit sont sont à un sommet du triangle : voir quadrilatère de Varignon.
Avec OA et OB centres des carrés de côtés [AB] et [AC] : voir quadrilatère de Varignon.
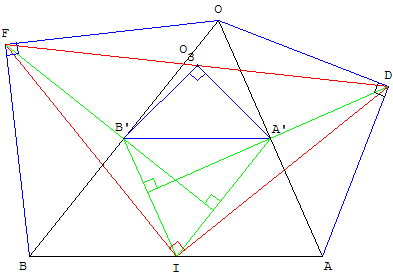
A’ et B’ sont les milieux de [OA] et [OB].
On construit B’O3A’ triangle direct rectangle isocèle en O3.
Montrer que le point O3 est le milieu [DF] ;
que (DA’) est orthogonale à (IB’) ;
ainsi que (FB’) est orthogonale à (IA’).
![]() Télécharger la figure GéoPlan tr_boa_7.g2w
Télécharger la figure GéoPlan tr_boa_7.g2w
Indications
Pour O3 milieu de [DF], démonstration avec deux triangles rectangles isocèles autour de B’O3A’ : voir 3.
[IB’], droite des milieux de BOA, et parallèle à (AO).
(DA’), médiane du triangle isocèle DOA, en est aussi la hauteur.
(DA’), perpendiculaire à (OA), est aussi perpendiculaire à (IB’).
Problèmes d'incidence
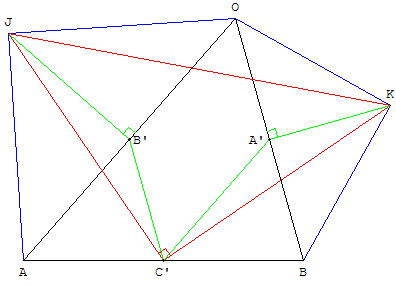
CAPES externe, épreuve sur dossier 2005
Étude d'une configuration à l'aide des triangles isométriques
Données :
un triangle BOA ;
OKB triangle rectangle isocèle en K “extérieur” au triangle BOA ;
OJA triangle rectangle isocèle en J “extérieur” au triangle BOA ;
A’, B’ et C’ les milieux des segments [OB], [OA] et [AB].
a. – Construire la figure sur un écran de calculatrice et l'animer.
b. – Conjecturer la nature du triangle KC’J.
c. – Montrer que les triangles A’C’K et A’B’J sont isométriques.
d. – Démontrer la conjecture émise.
Après avoir résolu et analysé cet exercice
a. – Présenter la figure réalisée sur la calculatrice.
b. – Dégager les méthodes et les savoirs mis en jeu.
c. – Proposer un autre exercice sur le même thème au niveau de la classe de seconde et dont la résolution fait appel aux triangles isométriques ou aux triangles semblables.
![]() Télécharger la figure GéoPlan incidence_capes_05.g2w
Télécharger la figure GéoPlan incidence_capes_05.g2w
B.5. La médiane de l'un est la hauteur de l'autre
Classe de première S
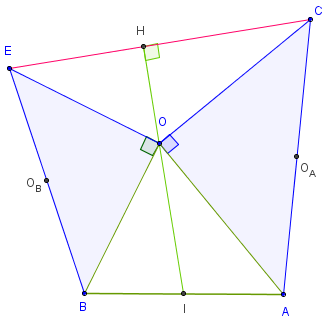
Énoncé :
OAB est un triangle quelconque, OAC et OEB sont deux triangles rectangles en O, isocèles directs.
Soit I le milieu de [AB].
Montrer que la médiane [OI] de BOA est hauteur du triangle ECO et que CE = 2 OI.
Démonstrations :
• Utilisation d'un produit scalaire
La forme vectorielle du théorème de la médiane permet d'écrire 2 ![]() =
= ![]() +
+ ![]()
et on a ![]() =
= ![]() −
− ![]() .
.
Calculer le produit scalaire 2 ![]() .
. ![]()
• Utilisation des complexes en Terminale S : dans un repère d'origine O, les affixes des points sont notées par les minuscules correspondantes.
![]() a pour affixe z = (a + b)/2 et
a pour affixe z = (a + b)/2 et
![]() pour affixe c − e = i (a + b) donc (c−e)/z = 2i. Ce qui permet de conclure.
pour affixe c − e = i (a + b) donc (c−e)/z = 2i. Ce qui permet de conclure.
• Utilisation d'une rotation de centre O
B.5.b. Symétrique d'un sommet par rapport à O
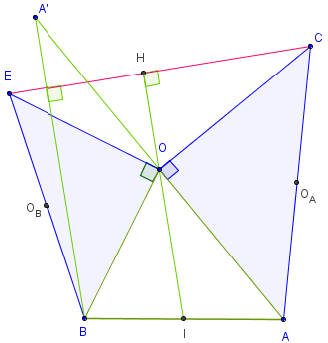
Introduire le symétrique A’ du point A par rapport à O.
La rotation de centre O d'angle ![]() transforme E en B, C en A’ et [EC] en [BA’].
transforme E en B, C en A’ et [EC] en [BA’].
Conclure avec (OI) droite des milieux du triangle ABA’ (homothétie de centre A et de rapport ![]() !).
!).
Dualité : de même si J est le milieu de [CE], la médiane [OJ] de ECO est hauteur [OK] du triangle BOA et AB = 2 OJ.
Remarques : Voir aussi l'exploitation des carrés COAD et BOEF complétant les deux triangles rectangles isocèles dans la page carrés autour de BOA.
De cette figure on peut ne retenir que les milieux de [BE] et [AC], voir la construction des deux triangles rectangles isocèles.
Pour un calcul avec produit scalaire, lorsque BOA est un triangle rectangle : voir similitudes au bac.
![]() Figures interactives dans GeoGebraTube : médiane de l'un, hauteur de l'autre
Figures interactives dans GeoGebraTube : médiane de l'un, hauteur de l'autre
B.6. autour d'un triangle

À l'extérieur d'un triangle, construire trois triangles rectangles isocèles dont les hypoténuses sont les côtés du triangle.
OA, OB et OC sont les sommets des demi-carrés construits à l'extérieur du triangle BOA.
Point de Vecten
Les segments [AOA] et [OBOC] sont de même longueur et perpendiculaires.
Il en est de même de [BOB] et [OAOC], ainsi que [COC] et [OAOB].
Les droites (AOA), (BOB) et (COC), hauteurs du triangle CDE sont concourantes en son orthocentre H.
H est le point de Vecten du triangle ABC.
OAOBOC est le triangle de Vecten du triangle ABC.
![]() Figure interactive dans GeoGebraTube : trois triangles rectangles isocèles autour d'un triangle
Figure interactive dans GeoGebraTube : trois triangles rectangles isocèles autour d'un triangle
Voir trois carrés autour d'un triangle (avec les démonstrations)
B.6.b. Théorème de Neuberg
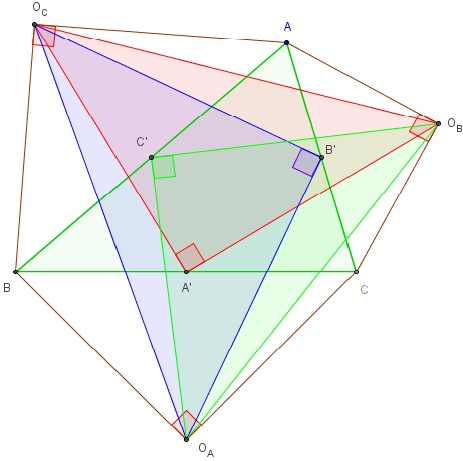
Six triangles rectangles isocèles
Si A’, B’, C’ sont les milieux des côtés de ABC, nous vu au paragraphe B.4 que les triangles OBA’OC, OAB’OC et OAC’OB sont rectangles isocèles.
![]() Figure interactive dans GeoGebraTube : théorème de Neuberg avec six triangles rectangles isocèles
Figure interactive dans GeoGebraTube : théorème de Neuberg avec six triangles rectangles isocèles
Voir la figure du théorème de Neuberg avec six centres de carrés.
B.7. Quatre triangles rectangles isocèles autour d'un quadrilatère
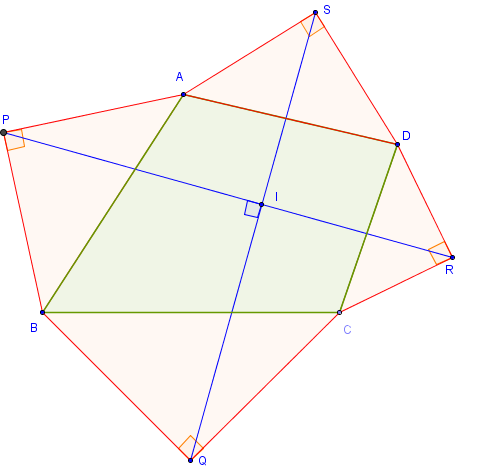
Quatre triangles rectangles isocèles à l'extérieur d'un quadrilatère ABCD.
Théorème de Van Aubel :
les segments [PR] et [QS], qui joignent les sommets des angles droits des triangles rectangles opposés, sont orthogonaux et de même longueur.
Si ABCD est un quadrilatère convexe, le quadrilatère PQRS est un pseudo-carré.
Démonstration :
les points P, Q, R et S sont les centres de quatre carrés autour du quadrilatère.
![]() Figure interactive dans GeoGebraTube : figure de Van Aubel avec 4 triangles rectangles
Figure interactive dans GeoGebraTube : figure de Van Aubel avec 4 triangles rectangles
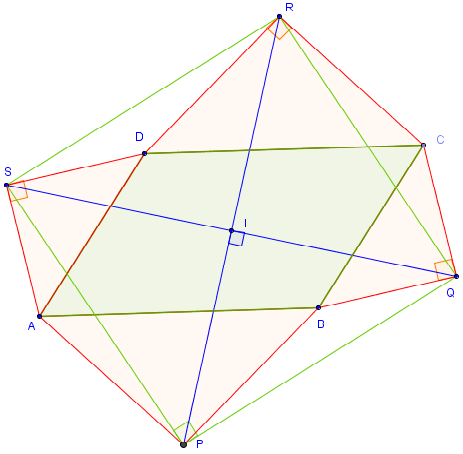
Quatre triangles rectangles isocèles à l'extérieur d'un parallélogramme ABCD.
Le quadrilatère PQRS formé par les sommets des angles droits est un carré.
![]() Figure interactive dans GeoGebraTube : théorème de Thébault avec 4 triangles rectangles isocèles
Figure interactive dans GeoGebraTube : théorème de Thébault avec 4 triangles rectangles isocèles
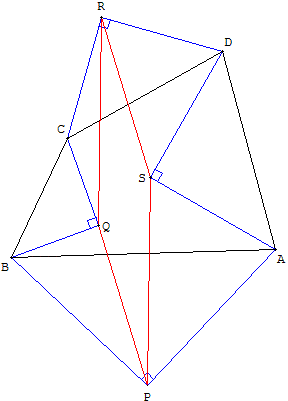
Construction de quatre triangles rectangles isocèles, alternativement indirects (BCQ et DAS) et directs (ABP et CDR), sur les côtés d'un quadrilatère ABCD.
PQRS est un parallélogramme.
![]() Télécharger la figure GéoPlan qu_trian_isocele.g2w
Télécharger la figure GéoPlan qu_trian_isocele.g2w
Voir : quatre triangles équilatéraux autour d'un quadrilatère
Partie C. Triangles équilatéraux
C.1. Quatre triangles équilatéraux
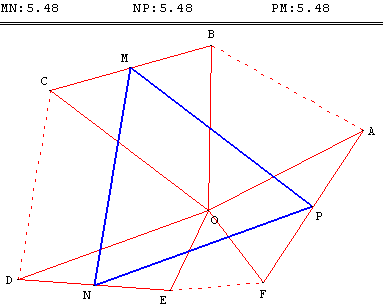
OAB, OCD et OEF sont trois triangles équilatéraux directs disjoints, sans chevauchement, n'ayant que le point O en commun.
Montrer que les milieux M, N et P des segments [BC], [DE] et [AF] forment un triangle équilatéral.
Solution

![]() Télécharger la figure GéoPlan tr_equi.g2w, la figure GéoPlan tr_equi_b.g2w
Télécharger la figure GéoPlan tr_equi.g2w, la figure GéoPlan tr_equi_b.g2w
Composé d'une translation et d'une rotation
Rappel : la composée d'une translation t et d'une rotation r(O, θ), distincte de l'identité, est une rotation d'angle θ.
En effet, c'est une isométrie directe et l'angle d'un vecteur ![]() et de son transformé
et de son transformé ![]() est θ.
est θ.
t |
r(O, θ) | |||
| G | → |
G1 | → |
G’ |
| H | → |
H1 | → |
H’ |
| A | → |
O | → |
O |
Si l'image du centre O, par la translation réciproque t ![]() , est le point A, la rotation composée transforme A en O, son centre I est situé sur la médiatrice de [AO] (À l'intersection avec l'arc capable d'angle θ).
, est le point A, la rotation composée transforme A en O, son centre I est situé sur la médiatrice de [AO] (À l'intersection avec l'arc capable d'angle θ).
Solution
On commence par compléter les parallélogrammes OBIC, ODJE et OFKA avec les points I, J et K symétriques de O par rapport à M, N et P.
Le triangle OAB est équilatéral : la rotation r(A, 60°) transforme B en O.
• Le triangle IAD est équilatéral.
En effet, I a pour image D par la succession de la transformation qui amène B en O (donc I en C) et de la rotation de 60° de centre O.
Cette transformation est d'ailleurs une rotation d'angle 60°, et, comme elle amène B en O, c'est une rotation de centre A.
t |
r(O, 60°) | |||
| I | → |
C | → |
D |
| B | → |
O | → |
O |
I a pour image D dans cette rotation r(A, 60°) : le triangle IAD est équilatéral.
La rotation r(I, 60°) transforme D en A.
• Le triangle IJK est équilatéral.
Par ailleurs, la succession de la translation amenant D en O (et donc J en E), de la rotation d'angle 60° de centre O et de la translation qui amène O en A (et donc F en K) transforme D en A et J en K.
Cette suite de trois transformations est donc la rotation d'angle 60° de centre I.
t |
r(O, 60°) | t |
||||
| D | → |
O | → |
O |
→ |
A |
| J | → |
E | → |
F |
→ |
K |
J a pour image K dans cette rotation r(I, 60°) : le triangle IJK est équilatéral.
• Le triangle MNP est équilatéral.
Comme MNP n'est rien d'autre que l'image réduite de IJK, dans un rapport de ![]() , par l'homothétie h(O,
, par l'homothétie h(O, ![]() ), MNP est lui aussi équilatéral.
), MNP est lui aussi équilatéral.
TS : Démonstration par calcul d'affixes de complexes.
Les affixes des points sont notées par les minuscules correspondantes, l'origine est en O.
Soit k = eiπ/3, on a : b = ka, d = kc et f = ke.
Sachant que 2m = b + c, 2n = d + e et 2p = f + a,
et en tenant compte de 1 − k + k2 = 0 et k3 = −1, on calcule :
2(n − m) = d +e − b − c = kc + e − ka − c = −ka + k2c + e,
2(p – m) = f + a − b − c = ke + a − ka − c = − k2a − c + ke.
On a donc p – m = k(n − m) et PQR est bien équilatéral.
Variante de l'exercice résolu ci-dessus :
Des symétries

Soit A, B, C, D, E, F six points pris, dans cet ordre sur un cercle de centre O, tels que les triangles OAB, OCD, OEF soient équilatéraux.
M est le milieu de [BC], N celui de [DE] et P celui de [FA].
Quelles symétries présente le triangle MNP ?
![]() Télécharger la figure GéoPlan mon_439.g2w
Télécharger la figure GéoPlan mon_439.g2w
Solution : télécharger la figure GéoPlan mon_439b.g2w
Voir hexagramme : cercles en seconde
C.2.a. Trois triangles isocèles d'angles de 30°
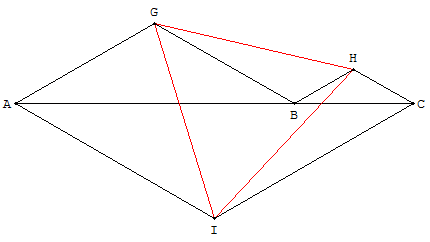
Sur un segment [AC] on place un point B de manière quelconque.
Au-dessus du segment on construit les triangles isocèles AGB et BHC d'angle au sommet 120°.
Au-dessous, le triangle isocèle AIC d'angle au sommet aussi égal à 120°.
Monter que le triangle GHI est équilatéral.
![]() Télécharger la figure GéoPlan mon_674.g2w
Télécharger la figure GéoPlan mon_674.g2w
Solution
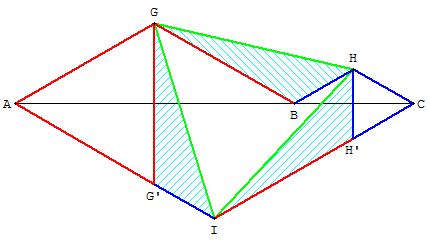
La solution tient en cette figure où l'on ajoute les symétriques G’ et H’ de P et Q par rapport à la droite (AB).
On montre aisément que les triangles AGG’ et CHH’ sont équilatéraux
et que AI = AG + CH.
On en déduit la coloration des segments rouges (tous égaux) et bleu (tous égaux).
Les triangles hachurés en bleu ciel, ayant tous un côté rouge et un côté bleu faisant entre eux un angle de 120°, sont isométriques.
On en déduit l'égalité des segments GH, HI et IG.
![]() Télécharger la figure GéoPlan mon_674s.g2w
Télécharger la figure GéoPlan mon_674s.g2w
C.2.b. Quatre autres triangles équilatéraux
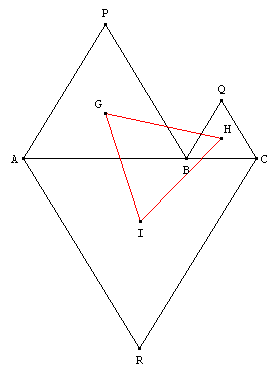
Cas particulier du triangle de Napoléon lorsque le triangle ABC est dégénéré (B situé sur le segment [AC])
Triangles équilatéraux
ABP, BCQ et CAR sont trois triangles équilatéraux directs.
Montrer que les centres de gravité G, H et I de ces triangles forment un triangle équilatéral GHI.
Solution
Soit ![]() la rotation vectorielle d'angle
la rotation vectorielle d'angle ![]() et O une origine.
et O une origine.
On calcule :
3![]() = 3
= 3![]() − 3
− 3![]()
3![]() =
= ![]() +
+ ![]() +
+ ![]() −
− ![]() −
− ![]() −
−![]()
3![]() =
= ![]() +
+ ![]() +
+ ![]() .
.
Donc : ![]() (3
(3![]() ) =
) = ![]() (
(![]() +
+ ![]() +
+ ![]() ) =
) = ![]() +
+ ![]() +
+ ![]()
![]() (3
(3![]() ) =
) = ![]() −
− ![]() +
+ ![]() −
− ![]() +
+ ![]() −
− ![]()
![]() (3
(3![]() ) = (
) = (![]() +
+ ![]() +
+ ![]() ) − (
) − (![]() +
+ ![]() +
+ ![]() )
)
![]() (3
(3![]() ) = 3
) = 3![]() − 3
− 3![]() = 3
= 3![]() .
.
On a donc ![]() (
(![]() ) =
) = ![]() ce qui signifie que GHI est équilatéral.
ce qui signifie que GHI est équilatéral.
![]() Figure interactive dans GeoGebraTube : quatre triangles équilatéraux
Figure interactive dans GeoGebraTube : quatre triangles équilatéraux
Problème proposé à l'épreuve pratique 2009 avec deux similitudes ayant pour composée la rotation de centre I : étude d'une figure du plan
Lieu du point M milieu de [PQ] : voir milieu des sommets de deux triangles équilatéraux
C.3. Trois triangles équilatéraux
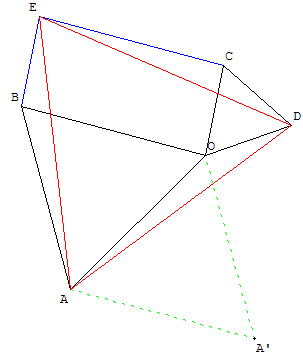
À partir de trois points O, A et C, tracer deux triangles équilatéraux directs OBA et ODC ayant le sommet O en commun, puis placer le point E tel que BOCE soit un parallélogramme.
Montrer que ADE est un triangle équilatéral.
Solution
Soit f la composée de la rotation d'angle 60° de centre O et de la translation qui amène O en B (et donc C en E) est une rotation d'angle 60°.
Soit A’ est l'image de A par la rotation. On a :
| r(O, 60°) | t |
|||
| A | → |
A’ |
→ |
A |
| D | → |
C |
→ |
E |
On a donc f(A) = A. f est la rotation de centre A et d'angle 60°.
Comme f(D) = E, le triangle ADE est bien équilatéral.
![]() Télécharger la figure GéoPlan tr_equi4.g2w
Télécharger la figure GéoPlan tr_equi4.g2w
Cas particuliers :
Rectangle : construire un rectangle BOCE et à l'extérieur deux triangles équilatéraux directs OBA et ODC.
ADE est un triangle équilatéral.
Carré : voir deux triangles équilatéraux autour d'un carré ci-dessous
C.4. Quatre triangles équilatéraux autour d'un quadrilatère

Construction de quatre triangles équilatéraux, alternativement directs (BCQ et DAS) et indirects (ABP et CDR), sur les côtés d'un quadrilatère ABCD.
En utilisant les rotations d'angle ![]() , montrer qu'en prenant pour centre A,
le vecteur
, montrer qu'en prenant pour centre A,
le vecteur ![]() a pour image
a pour image ![]() et qu'en prenant pour centre C, le vecteur
et qu'en prenant pour centre C, le vecteur ![]() a pour image
a pour image ![]() .
.
Conclure que ![]() =
= ![]() .
.
PQRS est donc un parallélogramme, les longueurs de ses côtés sont égales aux longueurs des diagonales de ABCD.
![]() Télécharger la figure GéoPlan qu_trian.g2w
Télécharger la figure GéoPlan qu_trian.g2w
Voir : quatre triangles rectangles isocèles autour d'un quadrilatère
C.5. Deux triangles équilatéraux autour d'un carré
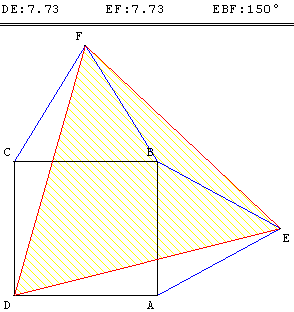
C.5.a. Un troisième triangle équilatéral
Victor Thébault 1882-1960
Sur deux côtés consécutifs d'un carré ABCD, on construit extérieurement à celui-ci deux triangles équilatéraux ABE et BCF.
Le triangle DEF ainsi formé est équilatéral.
Indication
Montrer que les triangles DAE et EBF sont isométriques :
• en calculant leurs angles en A et B (en classe de 3e),
• en utilisant une rotation de centre B et d'angle − 60° (en classe de 2nde).
![]() Figure interactive dans GeoGebraTube : deux triangles équilatéraux autour d'un carré
Figure interactive dans GeoGebraTube : deux triangles équilatéraux autour d'un carré

De même figure ci-contre, si l'on construit les deux triangles équilatéraux ABE et BCF à l'intérieur du carré, DEF est encore équilatéral.
Théorème de Thébault :
quatre carrés à l'extérieur d'un parallélogramme
le théorème de Thébault − Sawayama
Démonstrations, voir
WikiPédia : théorème de Thébault
C.5.b. Deux segments isométriques
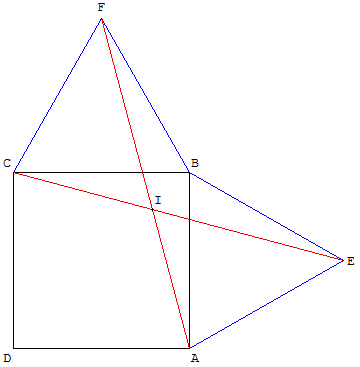
Sur deux côtés consécutifs d'un carré ABCD, on construit extérieurement à celui-ci deux triangles équilatéraux ABE et BCF.
Montrer qu'il existe une rotation qui transforme le segment [AF] en [CE].
En déduire que AF = CE et l'angle AÎE.
Quel est l'axe de symétrie de la figure ?
En déduire un alignement.
Indications
La rotation de centre B et d'angle 60° transforme A en E, F en C, [AF] en [EC].
L'angle des droites (AF) et (CE) est donc de 60°.
La droite (BD) est axe de symétrie de la figure.
Le carré est globalement invariant et la symétrie échange les triangles équilatéraux.
Le point A a pour image C et F a pour image E. L'image de la droite (AF) est (CE).
Le point d'intersection I de ces deux droites est situé sur l'axe de symétrie.
Les points B, D et I sont alignés.
![]() Télécharger la figure GéoPlan ca_trian2.g2w
Télécharger la figure GéoPlan ca_trian2.g2w
Démonstration

Rotation d'un triangle : par la rotation de centre B et d'angle 60°, le triangle BAF a pour image BEC, d'où AF = EC.
La médiatrice de [AB] est celle de [DC] ; elle passe par E,
d'où EC = ED.
La médiatrice de [AD] est celle de [BC] ; elle passe par F,
d'où AF = DF.
En conséquence, ED = DF.
Le triangle isocèle BAF a pour angle au sommet
ABF = 90° + 60° = 150°.
Les angles aigus mesurent (180° – 150°)/2 = 15°,
soit BFA = 15° et FAE = 15° + 60° = 75°.
Avec J milieu de [AE], FJA = 180° − 15° − 75° = 90°.
Le triangle FJA est rectangle et (FJ) est la médiatrice de [AE]
et AF = FE.
ED = DF = FE : le triangle DEF est équilatéral.
C.6. Triangles de Napoléon
Maths élém - Lebossé et Hémery - Géométrie - Rotations - 1961
Ces triangles sont attribués à l'empereur. D'après Henri Lebesgue, Lagrange lui aurait dit : « Mon Général, nous nous attendions à tout de vous, sauf à des leçons de géométrie ».
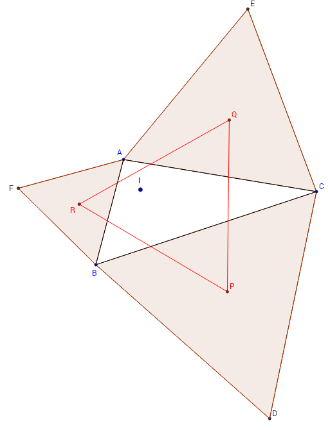
ABC est un triangle, dont tous les angles sont inférieurs à ![]() , bordé extérieurement par trois
triangles équilatéraux BCD, ACE et ABF ayant pour centres de gravité respectifs P, Q et R.:
, bordé extérieurement par trois
triangles équilatéraux BCD, ACE et ABF ayant pour centres de gravité respectifs P, Q et R.:
PQR triangle extérieur de Napoléon
Théorème de Napoléon :
le triangle PQR est équilatéral (triangle extérieur de Napoléon).
Les triangles ABC et PQR ont même centre de gravité G.
![]() GeoGebraTube : lien vers point de Fermat à la fn de la figure suivante ci-dessous
GeoGebraTube : lien vers point de Fermat à la fn de la figure suivante ci-dessous
WikiPédia : Point de Fermat ou de Torricelli
Point de Torricelli
– les segments [AD], [BE] et [CF] sont concourants en I, point de Torricelli du triangle ABC,
– du point I, on voit les trois côtés du triangle sous un même angle :
I est aussi appelé point de Fermat ou premier point isogonal, point X(13) de ETC,
– le point I est encore le point proximal qui réalise le minimum de la somme MA + MB + MC lorsque M décrit le plan (Théorème de Torricelli ou de Schruttka), les segments [IA], [IB] et [IC] forment entre eux des angles de ![]() .
.
![]() Figure interactive dans GeoGebraTube : point de Fermat
Figure interactive dans GeoGebraTube : point de Fermat
Cercles de Torricelli
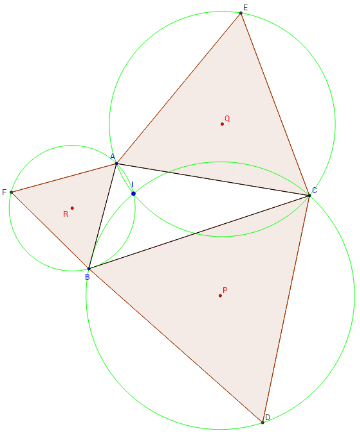
– les cercles, appelés cercles de Torricelli, circonscrits aux triangles BCD, ACE et ABF sont concourants en I (application du théorème du pivot de Forder démontré par Miquel en 1838).
![]() GeoGebraTube : lien vers point de Fermat à la fn de la figure ci-dessus
GeoGebraTube : lien vers point de Fermat à la fn de la figure ci-dessus
Premier point de Napoléon
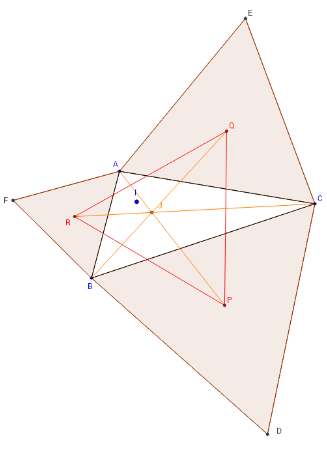
– Les céviennes (AP), (BQ) et (CR) (droites de Napoléon) sont concourantes en J, premier point de Napoléon ; X(17), dans ETC.
![]() GeoGebraTube : lien vers point de Fermat ci-dessus
GeoGebraTube : lien vers point de Fermat ci-dessus
En géométrie avant l'informatique, contrairement à certaines propriétés numériques, il n'était pas possible d'envisager toutes les situations possibles. D'une figure on ne pouvait déduire de preuve expérimentale en raison de l'imprécision du dessin d'une part et de l'ambiguïté de tracer un cas particulier et non une configuration générale d'autre part. Il fallait faire une démonstration abstraite soit avec la méthode synthétique (géométrie pure) qui remonte à Euclide qui, à partir des postulats et théorèmes établis précédemment, permet de déduire les propriétés cherchées, soit avec la méthode analytique, développée par Descartes, qui ramène la démonstration à des calculs algébriques.
Le logiciel GéoPlan permet de confier à l'ordinateur les calculs algébriques et de démontrer une propriété par une figure bien faite (à la précision de l'ordinateur près) et modifiable à volonté permettant d'envisager toutes les situations possibles.
Le problème de Napoléon a été posé par Fermat et résolu par Torricelli ; en classe de terminale S, sa démonstration se fera en utilisant les nombres complexes. Une résolution à l'aide de rotations est plus délicate : elle suppose l'intervention d'une composée de rotations, notion peu familière pour la plupart des élèves (brochure d'accompagnement des programmes de TS).
Triangle intérieur de Napoléon
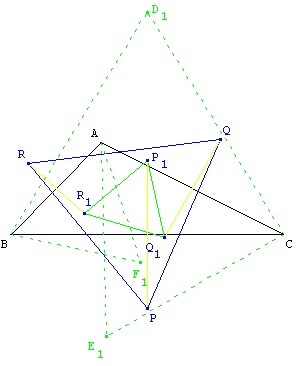
Triangle intérieur de Napoléon : c'est le triangle analogue P1Q1R1, obtenu en traçant trois triangles équilatéraux BCD1, ACE1 et ABF1, du même côté que le triangle ABC par rapport aux droites (AB), (BC) et (AC).
Les sommets P1, Q1, R1 du triangle intérieur sont les symétriques des sommets du triangle extérieur P, Q, R par rapport aux côtés [BC], [AC], [AB] du triangle ABC.
– la différence des aires entre le triangle extérieur PQR et le triangle intérieur P1Q1R1 est égale à l'aire du triangle ABC (démontré par Yaglom).
Théorème de Napoléon
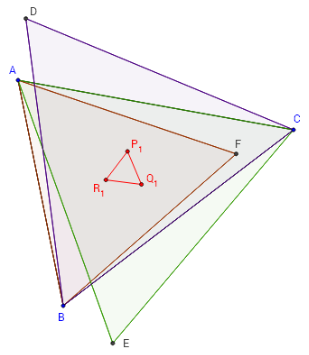
le triangle intérieur de Napoléon est équilatéral.
![]() Figure interactive dans GeoGebraTube triangle intérieur de Napoléon
Figure interactive dans GeoGebraTube triangle intérieur de Napoléon
Deuxième point isogonique
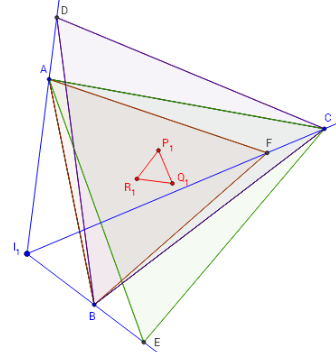
– les céviennes [AD], [BE] et [CF] sont concourants en I1,
deuxième point isogonique du triangle ABC,
point X(14) de ETC.
La droite de Fermat joint les deux points de fermat-Torricelli X(13)- X(14).
![]() GeoGebraTube :lien vers triangle intérieur de Napoléon figure ci-dessus
GeoGebraTube :lien vers triangle intérieur de Napoléon figure ci-dessus
Deuxième point de Napoléon
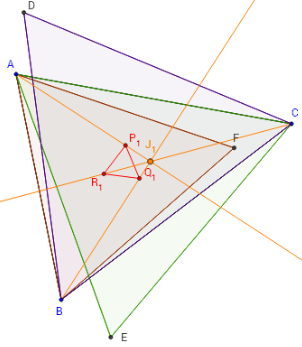
– Les céviennes (AP1), (BQ1) et (CR1) sont concourantes en J1,
deuxième point de Napoléon ;
X(18), dans ETC.
La ligne de Napoléon joint les deux points de Napoléon X(17)-X(18)
![]() Figure interactive dans GeoGebraTube : triangle intérieur de Napoléon
Figure interactive dans GeoGebraTube : triangle intérieur de Napoléon
Calculs en choisissant le point I comme origine et la droite (AD) comme axe des abscisses, voir plan complexe
Autres travaux de Miquel, configuration du quadrilatère complet, voir : plan projectif
Retrouver le centre d'un cercle au « compas seul » : problème de Napoléon
D. BOA isocèle
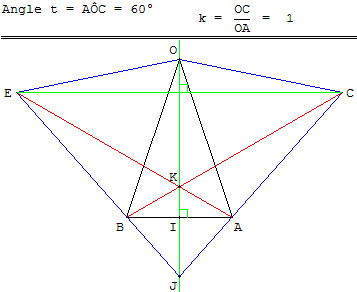
Autour d'un triangle isocèle BOA,
construction de deux triangles isométriques OAC et OEB,
à l'extérieur du triangle BOA.
I est le milieu de [AB],
J l'intersection de (AC) et (BE),
K l'intersection de (BC) et (AE).
Montrer que les points O, I, K, J sont alignés,
que la droite (CE) est parallèle à (AB).
![]() Télécharger la figure GéoPlan is_boa_1.g2w
Télécharger la figure GéoPlan is_boa_1.g2w
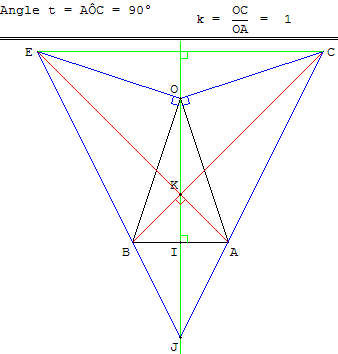
Construction de deux triangles OAC et OEB, rectangles isocèles en O,
à l'extérieur du triangle BOA.
(BC) et (AE) sont alors orthogonales.
![]() Télécharger la figure GéoPlan is_boa_2.g2w
Télécharger la figure GéoPlan is_boa_2.g2w
Table des matières
|
Téléchargement
studylibfr.com/les-problèmes-du-boa---aix Google considère l'URL de ce document comme une erreur de type "soft 404" mais référence la copie. Copyright 2003 - © Patrice Debart |
|
Dans d'autres pages du site Les problèmes du BOA : rotation |
Chevrier, Dobigeon – La géométrie plane au lycée - IREM de Poitiers, 1989 - À qui j'ai emprunté le titre de cette page. Coxeter et Greitzer – Redécouvrons la géométrie - Éditions Jacques Gabay - 1971-1997 Pour un enseignement problématisé des mathématiques au lycée - 2003 - brochure APMEP no 150 Exercices dans de nombreux manuels scolaires. |
|
|
Page no 49, réalisée le 28/7/2003 |