Descartes et les Mathématiques
Rotation au collège
Faire opérer les transformations avec la géométrie dynamique.
Sommaire
1. Orthocentre d'un triangle inscrit dans un carré
2. Aire d'un polygone formé par l'intersection de deux carrés
Les problèmes du BOA - rotation d'un triangle
4. Construction de triangles rectangles isocèles autour d'un triangle BOA
Construction de triangles équilatéraux autour d'un triangle BOA
Lieu géométrique faisant intervenir une rotation : le carré variable
Classe de troisième d'avant 2008
Depuis 2008, l'étude des rotations est hors programme au collège.
Les éléments qui faisaient la chair des programmes de géométrie ont presque tous disparu, en particulier toutes les transformations : un bachelier scientifique ne saura bientôt plus ce qu'est une rotation, une homothétie, et à peine ce qu'est une translation, sans parler évidemment des similitudes. Bien sûr il y a encore les symétries axiales, et on sait qu'elles engendrent les isométries. Mais est-il permis de parler de composition ?
Daniel Perrin : La géométrie : un domaine hors-programme ?
APMEP : Bulletin vert no 496 – Novembre 2011
1. Orthocentre d'un triangle variable inscrit dans un carré
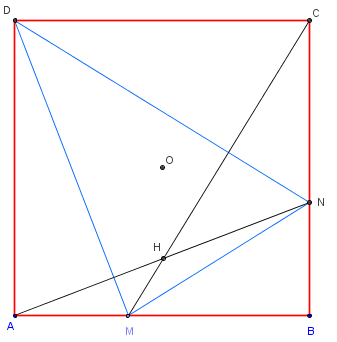
Sur les côtés [AB] et [BC] d'un carré ABCD, on place les points M et N
tels que AM = BN.
Soit H le point d'intersection de (AN) et (CM).
Montrer que H est l'orthocentre du triangle DMN.
Indications
Avec un logiciel de géométrie dynamique, tracer le carré ABCD, et placer un point M variable sur le segment [AB].
Avec l'outil compas, reporter la longueur AM sur [BC], placer le point N et tracer le triangle DMN et les deux hauteurs.
Démonstration
La rotation de centre O, centre du carré, et d'angle 90° transforme D en A et M en N.
Grâce à l'angle de la rotation, on déduit que le segment [DM] et son image [AN] sont perpendiculaires.
(AN) est une hauteur de DMN.
De même, par cette rotation, [CM] a pour image [DN].
(CM) est une deuxième hauteur de DMN et les droites (AN) et (CM) se coupent en H, orthocentre du triangle.
Figure interactive dans GeoGebraTube : orthocentre d'un triangle inscrit dans un carré
2. Aire d'un quadrilatère, intersection de deux carrés
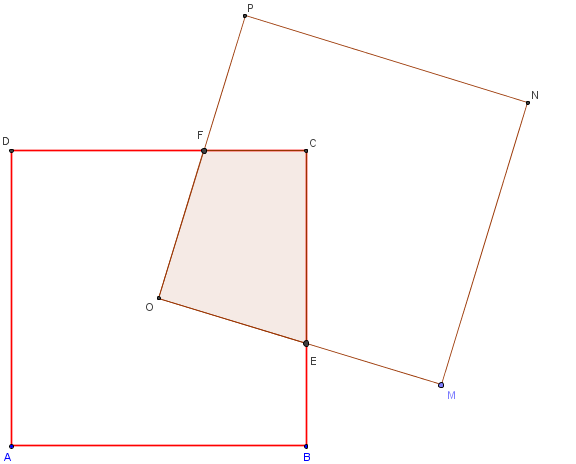
Étant donné un carré ABCD de centre O, on trace un second carré OMNP ayant un sommet en O, ce carré tourne autour du carré initial selon le polygone colorié sur la figure.
Indications
Avec un logiciel de géométrie dynamique, tracer le carré ABCD, et placer un point M variable sur un cercle (c) de centre O et rayon supérieur à OA.
Tracer le carré OMNP et les points E et F d'intersection des carrés.
En utilisant par exemple le sommet C, il est possible de tracer et de colorier le polygone OECF.
GeoGebra renvoie l'aire du quadrilatère.
En déplaçant M dans l'angle BÔC, on remarque que l'aire est constante et est égale au quart de l'aire du carré initial.
Démonstration
Par la rotation de centre O et d'angle 90° B a pour image C et E a pour image F et le triangle OBE est isométrique du triangle OCF.
Aire(ABCD)
= Aire(OBC) = Aire(OBE) + Aire(OEC)
= Aire(OEC) + Aire(OCF) = Aire(OEF).
Figure interactive dans GeoGebraTube : aire d'un quadrilatère intersection de deux carrés
3. Carré et rotation
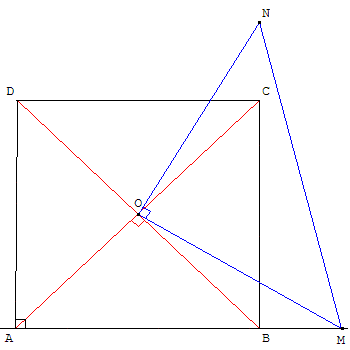
Soit M un point variable sur la droite (AB) qui borde le carré ABCD de centre O.
À partir de M, on construit le triangle isocèle OMN, rectangle en O.
Montrer que les points B, C et N sont alignés.
Indication
• Utilisation d'une rotation de centre O et d'angle 90° :
Les trois points alignés A, B et M ont pour image B, C et N, qui sont donc alignés.
Télécharger la figure GéoPlan carre_rotation.g2w
4. Deux triangles isocèles à l'extérieur d'un triangle
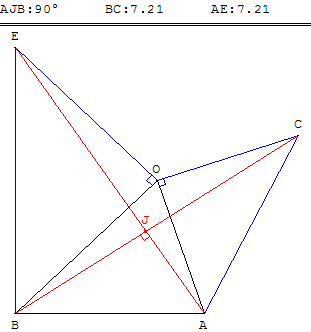
Construction de deux triangles rectangles isocèles.
Paragraphe extrait de la page : les problèmes du BOA
BOA est un triangle quelconque, OAC et OEB sont deux triangles rectangles isocèles directs.
Montrer que les droites (AE) et (BC) sont perpendiculaires et que BC = AE.
Indications : rotation d'un triangle
Par la rotation de centre O et d'angle α = 90°, A a pour image C et E a pour image B, donc [AE] a pour image [CB].
Le triangle OAE a pour image OCB.
Comme la rotation est une isométrie, on a AE = CB et vu que l'angle d'une droite et de sa transformée est égal à l'angle de la rotation,
on a AJC = α = 90°.
Télécharger la figure GéoPlan tr_boa_1.g2w
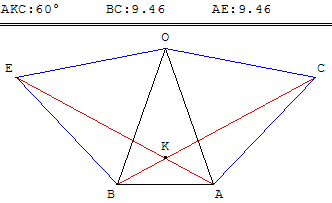
Autour d'un triangle isocèle BOA, construction de deux triangles équilatéraux OAC et OEB à l'extérieur du triangle BOA.
Montrer que BC = AE et vérifier que l'angle des droites (BC) et (AE) est de 60°.
Indications
Par la rotation de centre O et d'angle α = 60°, [AE] a pour image [CB].
Le triangle OAE a pour image OCB.
D'où AE = BC et l'angle de ces droites est égal de la rotation : AKC = 60°.
Télécharger la figure GéoPlan is_boa_3.g2w
Cas général - deux triangles isocèle semblables : voir les problèmes du BOA
Index transformations
Dans d'autres pages du site
Rotations : exercices de-ci, de-là : un triangle à la quatre-six-deux
Carré et deux triangles équilatéraux
Google friendly
Page no 167, créée le 20/2/2011
mise à jour le 28/10/2011