Descartes et les Mathématiques

Symétrie et rotation à la six-quatre-deux

Carré ou triangle à la six-quatre-deux : exercices de-ci, de-là en classe de seconde.

Depuis 2009, l'étude des rotations est hors programme de seconde.

Exercices de-ci, de-là

491-2 Un triangle à la quatre-six-deux

244. Un carré à la six-quatre-deux

680. Aire d'un jardin à la six-quatre-deux

Élisabeth Busser et Gilles Cohen
Copyright POLE 2001 - 2010

Locution adverbiale
À la six-quatre-deux : à la hâte, négligemment, sans plan !

Exercices de-ci, de-là

491-2 Un triangle à la quatre-six-deux

Énoncé de Jérôme Esquérré

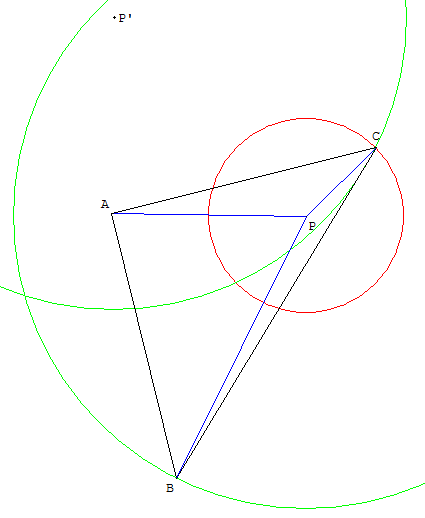
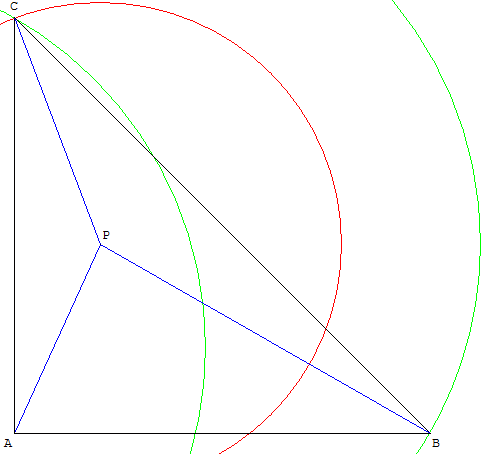
Construction du triangle à partir du point P

Soient A et P deux points du plan tels que AP = 4.
Construire le triangle rectangle isocèle en A tel que BP = 6 et CP = 2.

Indication

Utilisation de la rotation de centre A et d'angle 90° qui transforme le sommet B du triangle rectangle isocèle en C.

Tracer deux cercles (c₁) et (c₂) de centre P et de rayon 6 et 2.

Recherche avec GéoPlan

À partir d'un point M (non dessiné) du cercle (c₁), construire le triangle équilatéral AMM’. Déplacer le point M de telle façon que M’ soit sur le cercle (c₂). Vérifier que le lieu de M’ est un cercle.

Solution

La rotation de centre A et d'angle 90° transforme le cercle (c₁) en un cercle (c’) de centre P’, image de P par cette rotation.
On choisit le point C est à l'intersection des cercles (c₁) et (c’), de telle façon que P soit à l'intérieur de ABC.
B est alors l'image réciproque de C.

Télécharger la figure GéoPlan triangle-six-quatre-deux.g2w

244. Un carré à la six-quatre-deux

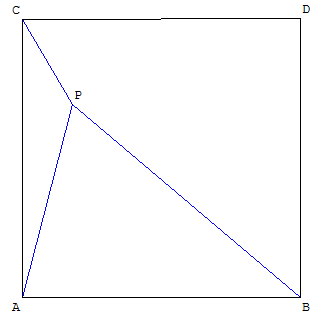
Le Monde, 16-23 octobre 2001

Énoncé

Sur un parchemin ne figure qu'un carré, trois segments et trois indications de longueur : 6, 4, 2…

Saurez-vous déterminer, par le raisonnement, l'angle APE ?

Indication

L'angle cherché mesure 135°.

Télécharger la figure GéoPlan carre-six-quatre-deux.g2w

Solution

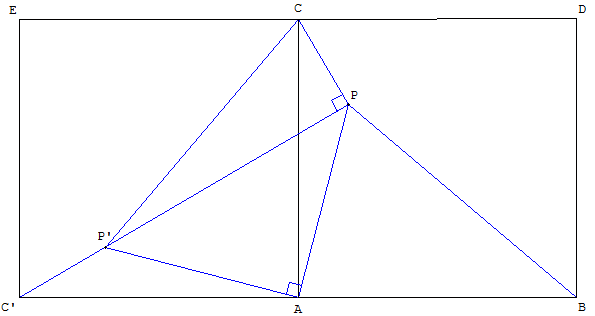
Une rotation de la figure autour du point A conserve les angles et les longueurs.
Soit P’ l'image de P par cette rotation.

Le théorème de Pythagore dans le triangle APP’, rectangle isocèle en A, permet de calculer la longueur PP’ = 4.
Comme CP’ = BP = 6, la réciproque de ce même théorème de Pythagore permet de monter que le triangle P’PD est rectangle en P.

L'angle APE mesure : 90° + 45° = 135°.

De plus les points P, P’ et C’ sont alignés :
en effet, dans le triangle rectangle APP’, (P’P) est perpendiculaire à (PC) ;
par la rotation (P’A) est perpendiculaire à (PC).
P’ et C’ sont alignés avec P sur la perpendiculaire à (PC) passant par P.

Télécharger la figure GéoPlan rectangle-six-quatre-deux.g2w

680. Un jardin à la six-quatre-deux

Le Monde magazine, 17-24 juillet 2010

Dessin du point P à l'intérieur d'un triangle rectangle isocèle

Le jardin d'Alice a la forme d'un triangle rectangle isocèle. Tandis qu'elle se tient au sommet de l'angle droit, Bob et Charlène se postent aux deux autres sommets.

Pierre quant à lui, est à l'intérieur, à quatre mètres d'Alice, à six mètres de Bob et à deux mètres de Charlène.

Quelle est l'aire du jardin ?

Recherche avec la géométrie dynamique

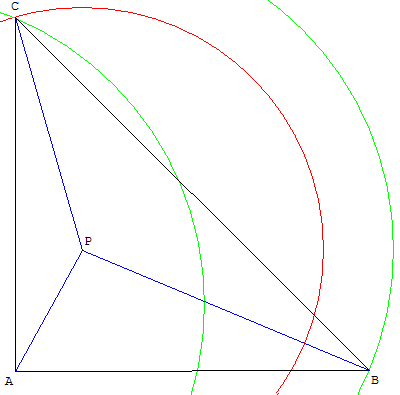
Le point P est le point d'intersection de trois cercles, centrés aux sommets A, B, et C du triangle, ayant pour rayons 4, 6 et 2.

Placer deux points B et C et tracer un triangle rectangle isocèle ABC (suffisamment grand).

Le cercle de centre A, de rayon 4, coupe de cercle de centre B, de rayon 6, en P (situé à l'intérieur du triangle).

Déplacer le point C de telle façon que le point P soit situé à une distance de C égale à 2.

Réponse : l'aire du jardin est 10 + 4, soit environ 15,66 m².

Télécharger la figure GéoPlan mon_680.g2w

De l'aire d'un pentagone à l'aire du triangle

  •  On commence par construire les symétriques Q, R et S du point P par rapport aux trois côtés du triangle. Ces points sont les points d'intersection des trois cercles, autres que P.

  •  Les angles sont « doublés » par les symétries :

R est l'image du point Q par la composée des deux symétries axiales d'axes (AB) et (AC). La composée est une rotation d'angle double de l'angle droit BÂC, donc RÂQ est un angle plat. R est donc le symétrique de Q par rapport à A.
On en déduit que RQ =8.

D'autre part les points R et Q sont les images de S par des composées des deux symétries axiales d'axes faisant des angles de 45°. Les composées sont des rotations d'angles doubles, soit 90°. RBS et SCQ sont des angles droits.

  •  On peut calculer RS = 6 et SQ = 2 comme hypoténuses des triangles rectangles isocèles RBS et QCS dont les aires sont donc 18 m² et 2  m².

  •  On remarque que RQ² + SQ² = 64 + 8 = (6)² = RS².
En conséquence, d'après la réciproque du théorème de Pythagore, RQS est un triangle rectangle et son aire est RQ × SQ/2 = 8.

  •  On obtient, par addition des aires des triangles RQS, RBS et QCS, l'aire du pentagone égale à 20 + 8 .
Il apparaît clairement, par les symétries, que ce pentagone a pour aire le double de celle du triangle ABC.

Télécharger la figure GéoPlan mon_680s.g2w

Autres angles de 135°

Christian Romon

Deux autres configurations où l'on trouve le même angle APC :

Un triangle à la quatre-neuf-sept

GéoPlan

Reprendre la figure du triangle à la quatre-six-deux
et modifier a = 4, b = 9 et c = 7.

Télécharger la figure GéoPlan triangle-quatre-sept-neuf.g2w

Un triangle à la six-onze-sept

Modifier a = 6, b = 11 et c = 7.

Télécharger la figure GéoPlan triangle-sept-six-onze.g2w