Descartes et les Mathématiques

Angles et rotations

Exercices de géométrie résolus avec des angles : cercle, arc capable, pivot.

1. Arc capable

Lieu d'où l'on « voit » un segment suivant un angle donné

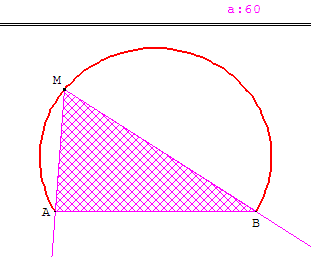
A et B sont deux points donnés du plan.

Le problème consiste à :
trouver l'ensemble L des points M du plan tels que l'angle (, ) soit égal à α.
(α donné en degrés entre −180° et 180°).

1.b. Construction de l'arc capable

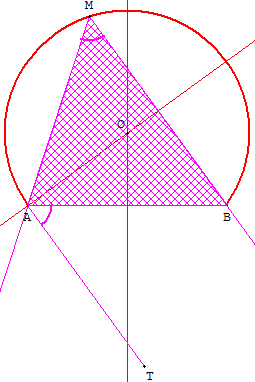
Reporter l'angle α le long de [BC) et on trouve une tangente [AT) au cercle circonscrit.
La perpendiculaire en B à cette tangente rencontre la médiatrice de [BC] en O, centre du cercle.

L'arc capable AMB est situé sur le cercle de centre O, passant par A.

C'est le lieu des points M d'où l'on « voit » le segment [AB] suivant l'angle α.

Angles inscrits

Lieux géométriques

2. Théorème du pivot

Premier théorème de Miquel

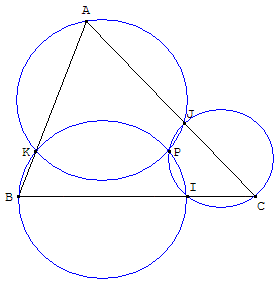
ABC est un triangle. Quels que soient les points I, J et K situés sur les côtés du triangle, les cercles circonscrits aux triangles AJK, BIK et CIJ sont concourants en un point P, pivot des trois points (dit aussi point de Miquel du triangle : X(501) de ETC.

Démontré en 1838 par A. Miquel, ce résultat fut dénommé théorème du pivot par Forder.

Théorème des trois cercles

Application réciproque : (c₁), (c₂) et (c₃) sont trois cercles concourants en P.

A est un point du cercle (c₁). Ce cercle recoupe (c₂) en K et (c₃) en J.
La droite (AK) recoupe le cercle (c₂) en B et la droite (AJ) recoupe le cercle (c₃) en C.

Si I est l'autre point d'intersection de (c₂) et (c₃), le théorème du pivot permet de montrer que les points B, I et C sont alignés.

Quadrilatère complet, point de Miquel, cercle de Miquel et points cocycliques : plan projectif

Point et cercle de Miquel : feuille de travail dynamique avec GeoGebra

Autres concours de cercle, démontrés par Miquel, voir : triangles de Napoléon

Théorème des cinq cercles : cercles en seconde

Figures exportées dans WikiPédia : théorème de Miquel

3. Un côté du triangle orthique et une tangente parallèles

ABC est un triangle et (c) son cercle circonscrit.
Les points B’ et C’ sont les pieds des hauteurs issues de B et C.
Montrer que la droite (B’C’) est parallèle à la tangente en A au cercle circonscrit (c).

Voir triangle orthique : « Les tangentes au cercle circonscrit passant par les sommets du triangle sont parallèles aux côtés du triangle orthique ».

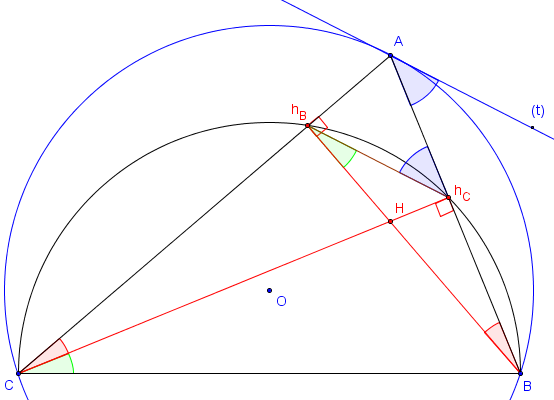
Solution

L'angle ACB inscrit dans le cercle (c) est égal à l'angle BÂt de la corde et de la tangente.
h_Bh_CA = h_Ch_BB + h_BBh_C.
Les points h_B’ et h_C sont situés sur le cercle (c’) de diamètre [BC].
Des égalités des angles inscrits h_BCh_C = h_BBh_C pour l'arc h_Bh_C et h_CCB = h_Ch_BB pour l'arc h_CB;
on déduit que :
ACB = h_BCh_C + h_CCB = h_BBh_C + h_Ch_BB = h_Bh_CA .

Les angles alternes-internes h_Bh_CA et BÂT sont égaux (égaux à ACB)
La droite (h_Bh_C) est parallèle à la tangente (At).

Figure interactive dans GeoGebraTube : Parallèle à un côté du triangle orthique

Application : montrer que les hauteurs d'un triangle sont concourantes ; démonstration d'Archimède : la géométrie du triangle.

4.a. Cordes de cercles tangents

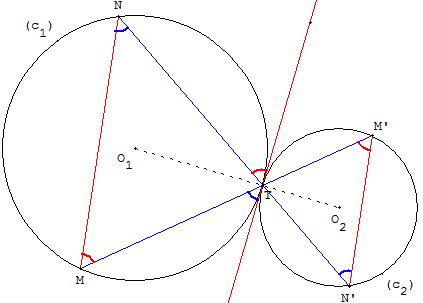
Deux cercles (c₁) de centre O₁ et (c₂) de centre O₂ sont tangents en T.
Deux droites, passant par T, coupent le cercle (c₁) en M et N, et le cercle (c₂) en M’ et N’.

Montrer que les droites (MN) et (M’N’) sont parallèles.

Solutions

Corde et tangente

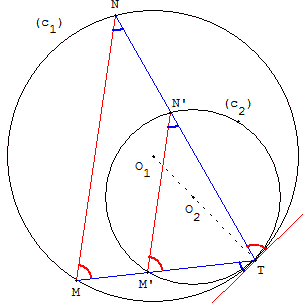
Dans les figures ci-dessus, d'après le théorème limite de cocyclicité on remarque que l'angle inscrit NMT est égal à l'angle de la corde [NT] et de la tangente en T.
Cet angle est aussi opposé à l'angle de la tangente ne T et de la corde [TN’] égal à l'angle inscrit N’M’T

Les angles NMT et N’M’T, alternes-internes, dans la figure de gauche, ou correspondants, dans la figure de droite, sont égaux. Les droites (MN) et (M’N’) sont parallèles.

Calcul d'angles au centre

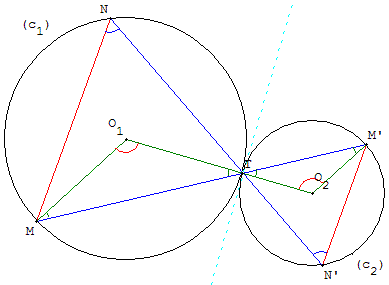
Les angles O₁TM et O₂TM’, opposés par le sommet, sont égaux.
Les triangles isocèles O₁TM et O₂TM’ sont donc semblables.
Les angles MO₁T et M’O₂T sont égaux.

Dans le cercle (c₁), l'angle inscrit MNT est égal à la moitié de l'angle au centre MO₁T,
dans (c₂), l'angle inscrit M’N’T est égal à la moitié de l'angle au centre M’O₂T.

Les angles MNT et M’N’T, alternes-internes dans la figure ci-contre sont égaux, les droites (MN) et (M’N’) sont parallèles.

Homothétie

En classe de première, utiliser l'homothétie h de centre T qui transforme (c₁) en (c₂). Par h, M’ est l'image de M, N’ est l'image de N, la droite (M’N’), image de (MN), est parallèle à (MN).

Voir l'utilisation de cette configuration pour tracer à la « règle et au compas » la parallèle à une droite passant par un point donné.

Voir aussi: lieu du transformé d'un point mobile sur un cercle

4.b. Recherche d'un point fixe

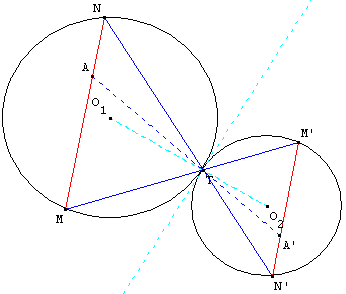
Soit O₁, O₂ et A trois points du plan et T un point à l'intérieur du segment [O₁O₂].

Deux cercles (c₁) de centre O₁ et (c₂) de centre O₂ sont tangents en T.
M est un point variable sur le cercle (c₁).
La droite (MT) recoupe le cercle (c₂) en M’.
La droite (MA) recoupe le cercle (c₁) en N.
La droite (NT) recoupe le cercle (c₂) en N’.

Les droites (MN) et (M’N’) sont parallèles.
Montrer que lorsque le point M varie, la droite (M’N’) passe par un point fixe A’.

Utiliser l'homothétie h de centre T qui transforme (c₁) en (c₂). A’ est l'image de A par h.

5. Alignement avec un point et son transformé par une rotation

Un point A fixe et un point M variable sont placés sur un cercle (c₁). Une rotation de centre A, d'angle t, transforme le cercle (c₁) en un cercle (c₂) et le point M en un point M’.

Les cercles (c₁) et (c₂) ont comme deuxième point d'intersection B.

Montrer que les points M, B et M’ sont alignés.

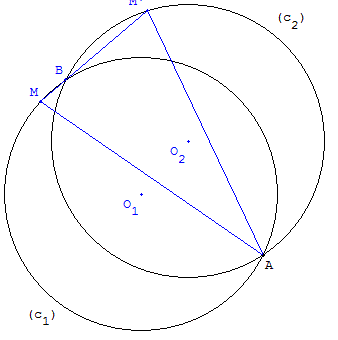
Le principe de démonstration est le suivant : le triangle AMM’ est isocèle (l'image de [AM] par la rotation est [AM’] donc AM = AM’) ; son angle au sommet A reste constant égal à l'angle t de la rotation ; il en est donc de même des angles en M et M’, les côtés [MA], [MM’] de l'angle en M découpent sur le cercle (c₁) un arc AB de longueur fixe ; l'extrémité B est donc un point fixe du cercle (c₁).
De même, la droite (MM’) passe par un point fixe du cercle (c₂).
La droite (MM’) passe par un point commun aux deux cercles : le point B, deuxième point d'intersection de ces cercles.

Réciproquement : soit deux cercles (c₁) et (c₂) de même rayon qui se coupent en A et B.
Si M et M’ sont les deux points diamétralement opposés à A, respectivement sur les cercles (c₁) et (c₂), alors les points M, B et M’ sont alignés.

Voir : Commeau - Géométrie maths élem - Masson, 1963 (mon livre de cours en terminale).

Démonstration avec les angles inscrits, voir : angles inscrits en troisième,

Pour deux cercles de rayons différents, voir le problème analogue avec une similitude.