 Descartes et les Mathématiques
Descartes et les Mathématiques
GéoPlan en quatrième
Six exercices de géométrie dynamique plane.
Sommaire
1. Médianes et centre de gravité
2. D'un triangle équilatéral à un triangle rectangle
3. Diamètres de deux cercles sécants : alignement - cocyclicité - concours
4. La ligne d'horizon
5. Trouver un milieu
6. Deux cercles
Dans d'autres pages du site
Retrouver un triangle à partir de droites remarquables
Retrouver un triangle à partir de centres ou de pieds
Lieux géométriques du milieu d'un segment
Constructions géométriques de tangentes au cercle
1. Médianes et centre de gravité
Les médianes sont les droites joignant les sommets d'un triangle aux milieux des côtés opposés. Les trois médianes sont concourantes au centre de gravité du triangle, situé aux ![]() de chaque médiane à partir du sommet correspondant.
de chaque médiane à partir du sommet correspondant.
Voici deux démonstrations du concours des médianes en classe de quatrième :
Parallélogramme de centre le centre de gravité
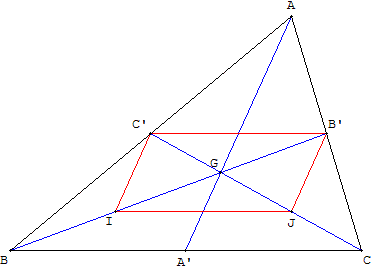
Soit G le point d'intersection des médianes [BB’] et [CC’] d'un triangle ABC.
I est le milieu de [BG] et J est le milieu de [CG].
Montrer que IJB’C’ est un parallélogramme.
En déduire que le point G est situé aux ![]() des médianes [BB’] et [CC’].
des médianes [BB’] et [CC’].
De même, en étudiant le parallélogramme IA’B’K où K est le milieu de [AG], on montre que les médianes [AA’] et [BB’] sont concourantes en un point situé à leurs ![]() . Ce point situé aux
. Ce point situé aux ![]() de [BB’], est donc le point G. Les trois médianes sont concourantes en ce même point G, centre de gravité du triangle.
de [BB’], est donc le point G. Les trois médianes sont concourantes en ce même point G, centre de gravité du triangle.
![]() Télécharger la figure GéoPlan medianes3.g2w
Télécharger la figure GéoPlan medianes3.g2w
Autres méthodes
Hexagone aux côtés opposés deux à deux parallèles,
somme des vecteurs ![]() +
+ ![]() +
+ ![]() : voir géométrie du triangle
: voir géométrie du triangle
Méthode des aires, voir : aire du triangle
Partage en trois de la diagonale d'un parallélogramme
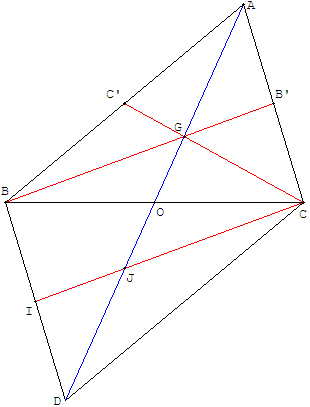
ABCD est un parallélogramme.
O, milieu de [BC] est le centre de symétrie du parallélogramme.
Les points B’, C’ et I sont les milieux des côtés.
Les points G et J sont les centres de gravité des triangles ABC et BCD.
Les points G et J partagent la diagonale [AD] du parallélogramme ABCD en trois segments égaux.
Démonstration
Avec la symétrie par rapport à O, on a AO = OD.
Le centre de gravité G est aux ![]() de la médiane [AO].
de la médiane [AO].
AG = ![]() AO =
AO = ![]() ×
× ![]() AD =
AD = ![]() AD.
AD.
De même DJ = ![]() DO =
DO = ![]() AD.
AD.
G et J partagent [AD] en trois parties égales.
Voir la figure d'Euclide : tiers de la diagonale d'un parallélogramme
![]() Télécharger la figure GéoPlan medianes4.g2w
Télécharger la figure GéoPlan medianes4.g2w
2. D'un triangle équilatéral à un triangle rectangle
Construire un triangle équilatéral basé sur le rayon d'un cercle, puis basé sur le diamètre, construire le triangle équilatéral double à l'aide d'un triangle rectangle d'angles aigus 60° et 30°. Où l'on retrouve la tangente à un cercle.
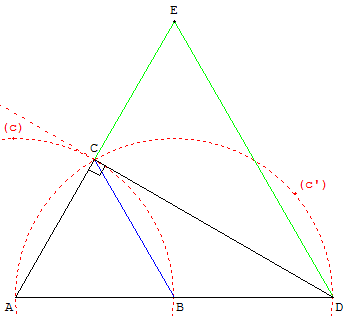
À partir de deux points A et B, construire un triangle équilatéral ABC.
Le point C est à l'intersection du cercle (c) de centre A passant par B et du cercle (c’) de centre B passant par A.
Soit D le symétrique de A par rapport à B, deuxième point d'intersection de (AB) et (c’).
Triangle rectangle
Le triangle ACD, inscrit le demi-cercle de diamètre [AD], est rectangle en C.
L'angle CAD mesure 60°, l'angle complémentaire ADC mesure 30°.
Si a est la longueur d'un côté du triangle équilatéral,
le triangle ADC a une hypoténuse de longueur 2a et BC = a![]() .
.
L'aire du triangle isocèle BCD est égale à l'aire du triangle équilatéral ABC (bases de même longueur a et même hauteur CH, où H est la projection, sur la droite (AB), du point C).
Grand triangle équilatéral
Le triangle rectangle ACD est la moitié du triangle équilatéral ADE, où E est le symétrique de A par rapport à C.
(CD) est une des médiatrices de ce triangle équilatéral.
Ce triangle ADE, de côté de longueur 2a, a une aire quatre fois plus grande que celle du triangle ABC.
Tangente
Cette figure permet de construire, sans équerre, la droite (CD), tangente en C au cercle (c) ; voir : cercle au collège
![]() Télécharger la figure GéoPlan tr_equi_rectangle.g2w
Télécharger la figure GéoPlan tr_equi_rectangle.g2w
3. Diamètres de deux cercles sécants
Alignement - cocyclicité
Alignement : trois points B, E et F sont alignés si les droites (BE) et (BF) sont perpendiculaires à une même troisième.
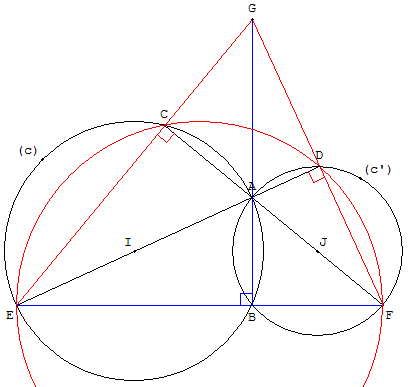
Deux cercles (c) et (c’) de centres distincts I et J sont sécants en A et B.
La droite (IA) recoupe le cercle (c) en E et le cercle (c’) en D.
La droite (JA) recoupe le cercle (c’) en F et le cercle (c) en C.
Alignement : les points E, B et F sont alignés.
Le triangle ABE est inscrit dans un demi-cercle, les droites (AB) et (BE) sont perpendiculaires.
On montre, de même, que la droite (AB) est perpendiculaire à (BF).
Ce qui permet d'en déduire l'alignement des points E, B et F.
Cocyclicité : les points E, C, D et F sont cocycliques
Le triangle ECA est inscrit dans un demi-cercle, les droites (EC) et (CA) sont perpendiculaires.
ECF est donc un triangle rectangle en C, inscrit dans le demi-cercle de diamètre [EF].
De même, le triangle ADE est rectangle en D.
Le triangle rectangle EDF est inscrit dans le demi-cercle de diamètre [EF].
Les quatre points E, C, D et F, inscrits dans le demi-cercle de diamètre [EF], sont cocycliques.
Concours
Montrer que les droites (AB), (EC) et (FD) sont concourantes.
Indications : configuration des hauteurs d'un triangle
Soit G le point d'intersection de (EC) et (FD). (ED) et (FC) sont deux hauteurs du triangle EFG. Le point A est l'orthocentre de ce triangle.
La droite (AB), perpendiculaire au côté [ E], est la troisième hauteur de ce triangle, concourante en G avec les deux côtés (EC) et (FD).
Terminale S : la similitude de centre A transformant E en F, transforme C en B et B en D. Le cercle (c) a pour image (c’).
![]() Télécharger la figure GéoPlan deux_cercles.g2w
Télécharger la figure GéoPlan deux_cercles.g2w
Autre figure : voir construction de deux triangles rectangles autour de BOA
Voir deux cercles sécants
Problème d'alignement, voir aussi : deux carrés
4. La ligne d'horizon
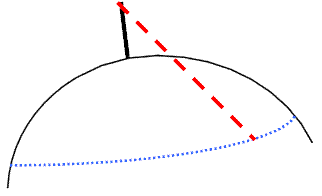
La plate forme du phare de la Hague (près de Cherbourg) est située à 52 mètres au-dessus de l'eau. Jusqu'à quelle distance un observateur, placé sur cette plate forme, peut-il espérer apercevoir un objet au ras de l'eau (par beau temps et mer calme) ?
Cette situation (problème de la ligne d'horizon) s'appuie sur la courbure de la surface de la sphère terrestre. Un travail préalable d'explicitation peut aider à bien appréhender le problème, avec une première schématisation « naïve ».
La modélisation proprement dite fait appel à la représentation de la sphère par un de ses grands cercles et fait donc passer de l'espace au plan.
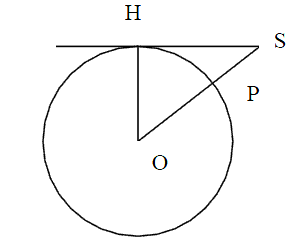
La longueur cherchée est la longueur de la tangente au cercle, issue du sommet S (P est le pied du phare). Le passage de la première représentation à la seconde est une démarche délicate qui peut nécessiter l'intervention de l'enseignant. C'est surtout l'occasion de développer la
capacité à substituer un problème plan à un problème de l'espace.
D'après le théorème de Pythagore appliqué au triangle SOH rectangle en H, SH2 = OS2 − OH2.
Deux directions d'exploitation se présentent :
1 - Le rayon de la sphère terrestre est approximativement de 6400 km, d'où le calcul à mener :
SH2 ≈ 6400,0522 − 64002, puis SH ≈25,8 km, solution approchée dont on peut se satisfaire dans le cadre du problème.
2 - Cette égalité peut être transformée en SH2 = (R+h)2 − R2, qui peut conduire à un travail, plus ambitieux mais accessible sur le plan du calcul, sur la transformation d'une expression algébrique. Nous obtenons aussi une expression qui permet d'obtenir la distance d'horizon pour n'importe quel phare (ou gratte-ciel ou aéronef !). La possibilité de faire varier h permet aussi de basculer naturellement dans le domaine des fonctions.
Ressources pour les classes de 6e, 5e, 4e et 3e - Géométrie au collège
Projet de document d'accompagnement mathématique - Juillet 2007
5. Trouver un milieu
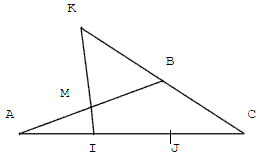
Dans le triangle ABC, M est le milieu de [AB] et I et J des points de [AC] tels que AI = IJ = JC = ![]() AC.
AC.
La droite (IM) coupe (BC) en K.
Montrer que B est le milieu de [KC].
6. Deux cercles
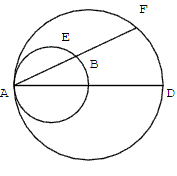
Soit le cercle (c) de centre B et de diamètre [AD] et le cercle (c’) de diamètre [AB].
F est un point de (c).
La droite (AF) coupe (c’) en E.
Montrer que E est le milieu de [AF].
Table des matières
Copyright 2007 - © Patrice Debart
Téléchargement
![]() Télécharger geometrie_quatrieme.pdf : ce document au format « .pdf »
Télécharger geometrie_quatrieme.pdf : ce document au format « .pdf »
![]() Mobile friendly
Mobile friendly
Dans d'autres pages du site
Exercices de géométrie au collège
GeoGebra 3D en 4e : Pyramide - Partition d'un cube
Page no 116, réalisée le 27/12/2007