Descartes et les Mathématiques
Exercices de géométrie au collège
Treize constructions avec GéoPlan ou GeoGebra : triangle, triangle rectangle, cercle et carré.
Sommaire
2. Points cocycliques dans un triangle
Dans d'autres pages du site
Tangentes communes à deux cercles
Carré et deux triangles équilatéraux
Constructions avec contraintes : recopier une figure
– Constructions à partir de trois droites remarquables
– Retrouver un triangle à partir de centres ou de pieds
Cercles - Feuerbach
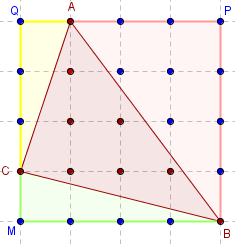
La planche à clous comme geoplan
Ne pas confondre le logiciel de géométrie dynamique, avec la construction de la planche à clous.
Problèmes sur les triangles permettant d'observer, d'analyser, pour le réinvestissement des connaissances sur les propriétés des figures de base.
1. Triangles rectangles
Un triangle inscrit dans un demi-cercle est un triangle rectangle.
1.a. Triangle de l'écolier
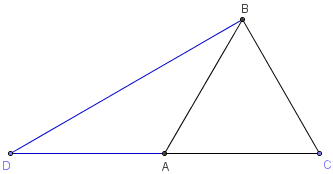
Triangle rectangle d'angles aigus de 30° et 60°.
ABC est un triangle équilatéral.
D est le symétrique de C par rapport à A.
– Montrer que BCD est un triangle rectangle.
Indications
Dans le triangle équilatéral ABC, l'angle en C est de 60° et AB = AC.
Par symétrie AD = AC.
D'où AB = AD = AC = 
DC. Le triangle BCD est rectangle en B.
ABD est un triangle isocèle d'angle au sommet BAD = 120°. Les angles aigus sont de 30°, donc BDC = 30°.
Réciproque
– Montrer que la médiane issue de l'angle droit d'un triangle de l'écolier le partage en un triangle équilatéral et un triangle isocèle.
Figure interactive dans GeoGebraTube : triangle de l'écolier
Une autre construction comme moitié d'un triangle équilatéral, voir : construction avec une équerre
1.b. Bissectrice et triangle rectangle
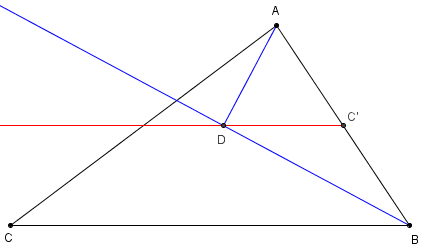
Dans un triangle ABC, la bissectrice de l'angle B et la parallèle au côté (BC), passant par le milieu C’ de [AB], sont concourantes en D.
– Montrer que les droites (BD) et (AD) sont perpendiculaires.
Indications
La bissectrice (BD) détermine les angles égaux CBD = DBA.
CBD = C’DB comme angles alternes-internes par rapport à la sécante (BD) et aux parallèles (BC) et (C’D).
C’BD est isocèle en C’ et C’D = C’B.
C’A = C’B car C’ est le milieu de [AB].
D'où C’D = C’B = C’A = AB. Le triangle ABD est rectangle en D. ADB est droit.
Figure interactive dans GeoGebraTube : triangle rectangle et bissectrice
2. Points cocycliques dans un triangle
Propriété réciproque : un angle droit est inscrit dans un demi-cercle.
Construction au compas seul
Ci-dessous une construction au compas avec des cercles définis par des points cocycliques.
Nous avons déjà rencontré ces figures dans le chapitre hauteur de la géométrie du triangle et elles permettent de démontrer les propriétés du triangle orthique ou avec le théorème de Clifford.
Projections du centre du cercle inscrit sur les côtés
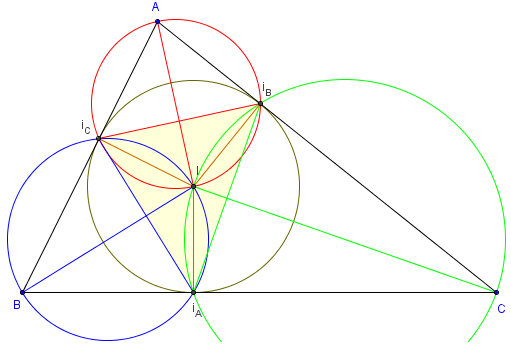
ABC est un triangle, les points iA, iB, iC sont les pieds des perpendiculaires issues du centre I du cercle inscrit sur les côtés [BC], [AC], [AB] du triangle.
– Le triangle iAiBiC s'appelle le triangle de Gergonne ou triangle de contact du triangle ABC.
– Les points I, A, iB, iC sont cocycliques sur le cercle de diamètre [IA],
(IA) est la médiatrice de [iB iC],
Les angles BAC et iCIiB sont supplémentaires.
– De même I, B, iA, iC sont cocycliques sur le cercle de diamètre [IB]
et les points I, C, iB, iC sont sur un même cercle de diamètre [IC].
Figure interactive dans GeoGebraTube : projections du centre du cercle inscrit
3. Triangles isocèles
3.a. Bissectrice d'un triangle et triangle isocèle
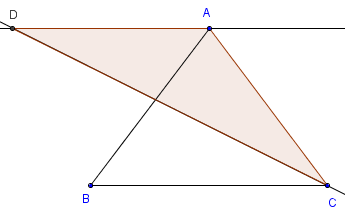
Dans un triangle ABC, la bissectrice de l'angle C et la parallèle au côté [BC], passant par le sommet A, sont concourantes en D.
– Montrer que le triangle ACD est isocèle.
Figure interactive dans GeoGebraTube : bissectrice et triangle isocèle
3.b. Carré et triangle équilatéral
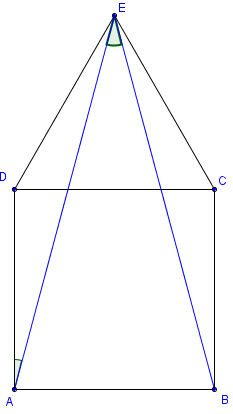
On reprend la figure d'un calcul d'angles.
ABCD est un carré.
CDE un triangle équilatéral tracé à l'extérieur du carré.
– quel est l'angle AEB ?
Indications
Montrer que le triangle DAE est isocèle.
Dire quel est l'angle obtus ADE.
En déduire la mesure des angles aigus DAE et DEA.
Conclure que l'angle AEB = 30° et que les angles à la base du triangle isocèle AEB mesurent 75°.
Figure interactive dans GeoGebraTube : carré et triangle équilatéral
3.c. Triangles isocèles, rectangle, équilatéral
On reprend la figure de l'alignement avec un carré et un triangle équilatéral.
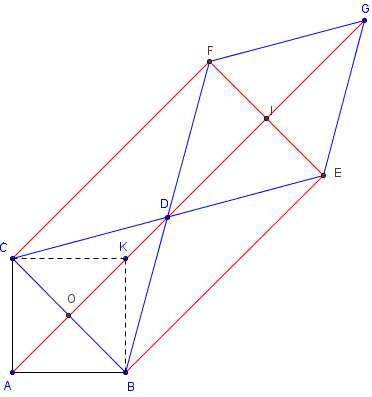
ABC est un triangle rectangle isocèle et BCD un triangle équilatéral.
La parallèle à (AD) passant par B coupe la droite (CD) en E.
Quelle est la nature du triangle BDE ? Du triangle BCE ?
Avec l'intersection F de (BD) avec la parallèle à (AD) passant par C, étudier de même les triangles CDF et CBF.
Montre que DEF est un triangle équilatéral et BEFC un rectangle.
On complète le parallélogramme EDFG. Montrer que c'est un losange et que les points A, O, D, I et G sont alignés.
Figure interactive dans GeoGebraTube : triangles et alignement
4. Carré, cercles et tangente
D'après « Activités significatives » – groupe collège de l'IREM de Toulouse – Bulletin no 392, février 1994.
Article exporté dans le wiki du MIAM..
Classe de 4e
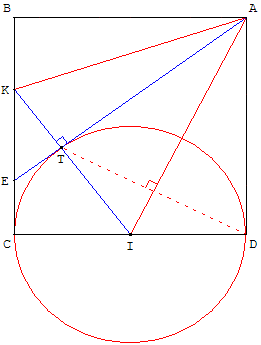
Tangente, bissectrice et angle de 45°.
1. ABCD est un carré, I le milieu de [CD]. Tracer le cercle (c1) de diamètre [CD] et le segment [IA].
Soit T le point symétrique de D par rapport à la droite (IA).
Que dire des triangles ADI et ATI ?
T est-il sur le cercle ? Justifier la réponse.
Que dire de la droite (AT) ?
2. La droite (IT) coupe (BC) en K.
Que dire des triangles ATK et ABK ?
Calculer l'angle IÂK.
Télécharger la figure GéoPlan carre_ce.g2w
Classe de 3e
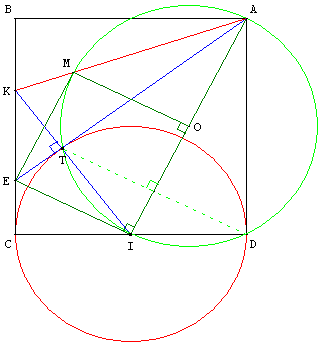
3. Les points A, T, I et D sont cocycliques et appartiennent au cercle (c2) de diamètre [AI]. Soit O milieu de [AI] son centre.
Soit M le deuxième point d'intersection de ce cercle et de la droite (AK).
Sur le cercle (c2) l'angle inscrit IÂM et l'angle au centre IÔM interceptent l'arc IM.
En déduire que l'angle IÔM est droit et que (MO) // (TD).
4. La droite (AT) coupe (BC) en E. Montrer que ET = EC.
5. Montrer que le quadrilatère OMEI est un carré.
Figure dans GeoGebraTube : carré, cercles et tangente
Indications
Soit 2a la longueur du côté du carré. Le cercle (c1) de centre I et diamètre [CD] a pour rayon a.
1. D a pour image T par la symétrie d'axe (IA). (IA) est la médiatrice de [DT], les droites sont perpendiculaires.
Par la symétrie d'axe (IA) les points I et A sont fixes et D a pour image T, [ID] a pour image [IT] donc IT = ID = a rayon du cercle (c1), le point T est sur le cercle. La symétrie transforme le triangle rectangle ADI en ATI. (AT) est perpendiculaire à (IT). La droite (AT) perpendiculaire au rayon [IT] est tangente au cercle (c1) en T.
(IA) est l'axe de symétrie du cerf-volant IDAT. Les angles DÂI et IÂT ont même mesure, IÂT = DÂT.
De même, les angles DÎA et AÎT sont égaux, (IA) est la bissectrice de DÎT.
Les côtés [AD] et [AT] des triangles rectangles ADI et ATI sont égaux au côté du carré : AD = AT = 2a.
D'après la propriété de Pythagore, l'hypoténuse AI2 = AD2 + DI2 = (2a)2 + a2 = 5a2. D'où AI = a
.
2. Les triangles rectangles ATK et ABK ont même hypoténuse [AK], les côtés AT et AB sont égaux à 2a.
Les deux triangles sont isométriques, d'où TK = BK et TÂK = KÂT.
(AK) est l'axe de symétrie du cerf-volant ATKB. TÂK = TÂB.
On a donc IÂT = DÂT et TÂK = TÂB, soit IÂK = IÂT + TÂK = (DÂT + TÂB) = DÂB = 90° = 45°.
3. Les triangles rectangles ADI et ATI sont inscrits dans le cercle de diamètre [AI]. Les points A, T, I et D sont cocycliques.
Pour l'arc IM du cercle (c2), l'angle inscrit IÂM = 45° est égal à la moitié l'angle au centre IÔM. L'angle IÔM = 2 × 45° est droit. Les droites (MO) et (DT), perpendiculaires à (IA), sont parallèles.
4. Les triangles rectangles ECI et ETI ont même hypoténuse [EI], les côtés CI et TI sont égaux à a. Les deux triangles sont isométriques, d'où EC = ET et CÎE = EÎT. (IE) est la bissectrice de CÎT.
5. (IE) et (IA) sont les bissectrices des angles supplémentaires CÎT et TÎD. Elles sont donc perpendiculaires. EÎO = 90°.
Les triangles rectangles ADI et IEC ont leurs côtés perpendiculaires, ils ont les mêmes angles : DÂI = CÎE.
cos(DÂI) = 
= 
= 
. CI = a et EI = 
= a
.
IO et OM sont deux rayons perpendiculaires du cercle (c2) égaux à a. Les côtés EI et OM de OMEI, perpendiculaires à IO sont parallèles et égaux. OMEI est un parallélogramme ayant un angle droit, soit un rectangle. La longueur est égale à la largeur a, c'est un carré.
5. Angle inconnu
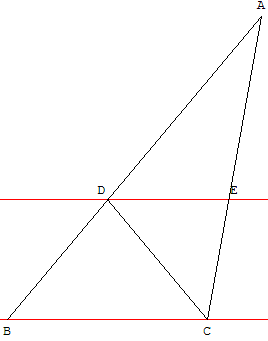
Angles dans un triangle
Dans cette figure, BAC = 30°, BD = CD et ED = EC.
Les droites (BC) et (DE) sont parallèles.
– Quelle est la mesure de l'angle ABC ?
Télécharger la figure GéoPlan angle_inconnu.g2w
Bissectrices d'un parallélogramme
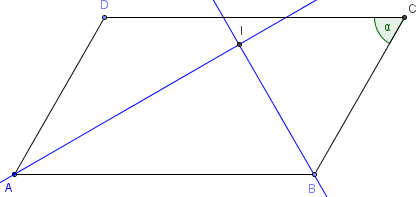
ABCD est un parallélogramme d'angle DAB = α.
Les bissectrices de l'angle A et de l'angle B sont concourantes en I.
– Quelle est la nature du triangle ABI.
Indications
L'angle BAI = α/2.
Le deuxième angle du parallélogramme est 180° − α,
donc ABI = 90° − α/2.
Dans le triangle ABI,
AIB = 180° − BAI − ABI = 180° − α/2 − (90° − α/2) = 90°.
L'angle est droit, le triangle ABI est rectangle en I, les bissectrices sont perpendiculaires.
Figure interactive dans GeoGebraTube : bissectrices d'un parallélogramme
Tâche impossible
Trouver un parallélogramme tel que les bissectrices de deux angles consécutifs ne soient pas perpendiculaires.
6. Prenons de la hauteur
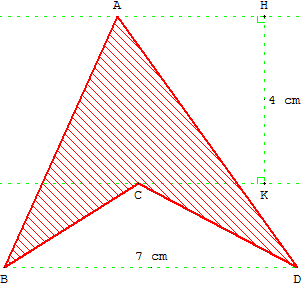
ABCD est un quadrilatère non convexe, non croisé.
Les points A et C sont situés sur deux droites (d) et (d’) parallèles, distantes de 4 cm.
B et D, distants de 7 cm, sont sur une troisième droite parallèle à (d) et (d’), située à une distance l de (d’).
– Quelle est l'aire du quadrilatère ?
Calcul
L'aire du quadrilatère est de 14 cm2, égale à la différence des aires des triangles ABD et CBD :
Aire(ABD) = × 7 × (4 + l) ; Aire(CBD) = × 7 × l.
Aire(ABCD) = × 7 × [(4 + l) − l] = × 7 × 4 = 14.
Télécharger la figure GéoPlan prenons_hauteur.g2w
Solution par la méthode des aires
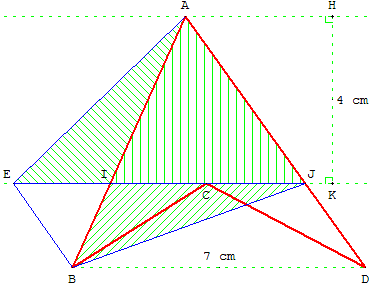
Soit I et J les points d'intersection de (AB) et (AD) avec (d’),
d'après la propriété du trapèze, on a : Aire(BCD) = Aire(BJD).
L'aire du quadrilatère est :
Aire(ABCD) = Aire(BAD) − Aire(BCD) = Aire(BAD) − Aire(BJD) = Aire(BAJ).
Soit E le point d'intersection de (d’) avec la parallèle à (AD) passant par B. BDJE est un parallélogramme et EJ = BD = 7 cm.
D'après le théorème du papillon, Aire(IJB) = Aire(IAE).
Donc, Aire(ABJ) = Aire(AIJ) + Aire(IJB) = Aire(AIJ) + Aire(IAE) = Aire(AEJ).
L'aire du quadrilatère est égale à l'aire du triangle AEJ,
soit × EJ × HK = × 7 × h = 14 cm2.
Généralisation
ABCD est un quadrilatère non convexe, non croisé, de diagonale extérieure [BD], si l est distance C à (BD) et l' la distance de A à (BD),
alors avec h = | l − l’ |, l'aire de ABCD est égale à × BD × h.
7. Hauteurs et médianes dans un triangle
Classes de quatrième - seconde
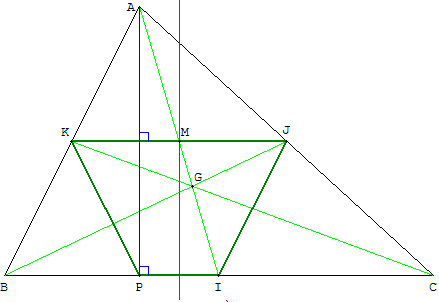
Trapèze isocèle inscrit dans un triangle
Dans un triangle ABC, P est le pied de la hauteur issue de A. Les points I, J et K sont les milieux des côtés.
– Montrer que le quadrilatère KPJI est un trapèze isocèle.
Indications avec des transformations
Les points A et P sont symétriques par rapport la droite des milieux (KJ).
[KP] et [KA] sont symétriques par rapport à (KJ).
Les segments [AI] et [KJ] se coupent en leur milieu M. Les points A et I d'une part, K et J d'autre part, sont symétriques part rapport à M. La symétrie de centre M transforme [KA] en [JI].
La composée des symétries par rapport à (KJ) et à M transforme [KP] en [JI] (par l'intermédiaire de [KJ]). Le résultat de la composition est la symétrie par rapport à la médiatrice de [KJ]. Cette médiatrice est l'axe de symétrie du quadrilatère KPJI qui bien un trapèze isocèle.
Télécharger la figure GéoPlan hauteur_mediane.g2w
8. Triangle et trapèze
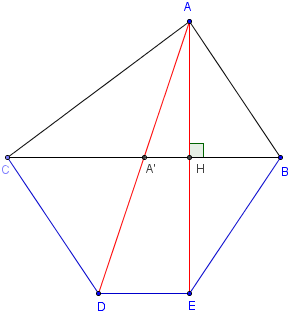
Soit ABC un triangle non isocèle en A, tel que AC > AB.
A’ est le milieu de [BC].
D est le symétrique de A par rapport à A’ et E le symétrique de A par rapport à (BC).
Trapèze isocèle
– Droite des milieux du triangle ADE : montrer que (DE) est parallèle à (BC).
– Symétries : montrer que CD et BE sont égaux à AB.
– En déduire que BCDE est un trapèze isocèle.
Figure interactive dans GeoGebraTube : triangle et trapèze
Table des matières
Mobile friendly
Téléchargement des anciennes version de 2008
Télécharger exercice_college.doc : ce document au format « .doc »
Télécharger exercice_college.pdf : ce document au format « .pdf » d'Adobe Acrobat
studylibfr/exercices-de-géométrie-au-collège
Copyright 2004 - © Patrice Debart
Page no 66, réalisée le 29/3/2004
modifiée le 27/6/2012