La reproduction de figures est aussi un exercice dans lequel la démarche d'analyse est essentielle. Dans ce type de problème, les contraintes sont données visuellement (la figure à reproduire) et la question de l'existence ne se pose pas : l'objet est déjà matérialisé.

L'analyse porte alors sur la reconnaissance de figures élémentaires de la configuration et sur l'articulation des tâches successives à mettre en œuvre pour arriver au résultat. Le niveau auquel la situation peut être proposée est déterminé par la complexité de la figure à élaborer et le temps donné pour le faire. Les exemples souvent rencontrés de reproduction de figures peuvent faire l'objet de travaux à tous les niveaux du collège à condition de disposer d'un temps suffisant (en dehors de la classe par exemple). Ces travaux peuvent être, d'autre part, différenciés suivant les élèves.

Ressources pour les classes de 6^e, 5^e, 4^e et 3^e - Géométrie au collège
Projet de document d'accompagnement mathématique - Juillet 2007

1. Tracer un ovale au tiers

Ovale elliptique ou anse d'architecte

Construction d'un demi-ovale défini par un diamètre de longueur KL = 2a.
Cette anse de panier dite égyptienne, à trois centres, relève d'une pratique élémentaire en collège.
La construction consiste à placer deux points I et J qui partagent le grand axe en trois parties égales.

Il semblerait que les architectes et autres tailleurs de pierre utilisent couramment l'anse KL.
Cette figure est une bonne adéquation à une ellipse de grand axe [KL].

Classe de sixième

constructions avec contraintes - anse de panier au tiers - copyright Patrice Debart 2008

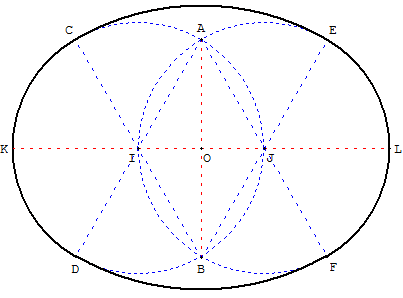
Tracer deux cercles de centre I, passant par J, et de centre J, passant par I.
Ces deux cercles se coupent en A et B.
Les diamètres, passant par A et B, recoupent les cercles en C, D, E et F.
Tracer les arcs de cercle de CD de centre I, EF de centre J, DF de centre A et CD de centre B.

Télécharger la figure GéoPlan ovale.g2w

Cette configuration fut utilisée pour la construction de ponts au fil des âges, et avec d'autres mesures, pour la construction des amphithéâtres romains.

Voir aussi : porte surmontée d'une anse de panier

Figure de Sébastien Leclerc

Figure dans GeoGebraTube : porte surmontée d'une anse de panier

2. Comment dessiner un œuf (géométrie)

Classe de troisième

Tracer un œuf au compas

constructions avec contraintes - dessiner un œuf - copyright Patrice Debart 2008

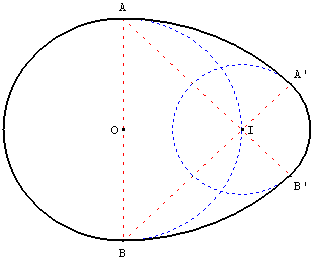
Dessiner un cercle de centre O et de rayon R = 3 ;

Soit I un point de ce grand cercle ; tracer le diamètre [AB] de ce grand cercle perpendiculaire à (OI) ;

Le cercle de centre A, passant par B rencontre [AI) en B’ :
ABI est un triangle rectangle isocèle : l'hypoténuse AB = AI ;
AB’ = 2R = AI + IB’ = R + IB’ ; soit IB’.= 2R − R

Le cercle de centre B, passant par A rencontre [BI) en A’ :
On trouve de même IA’ = BA’ − BI = 2R − R .
Le petit cercle, de centre I, passe par A’ et B’ a pour rayon r = 6 − 3.

La tracé de l'œuf s'obtient avec le grand demi-cercle BA ;
l'arc de centre A, d'extrémités B et B’ et d'angle 45°;
le petit arc de centre I, d'extrémités B’ et A’
l'arc de centre B, d'extrémités A’ et A et d'angle 45°.

Télécharger la figure GéoPlan œuf.g2w

Figure copiée par pinterest ; dessiner un oeuf
ou dessiner un oeuf
ou comment dessiner un oeuf

3. Arcs de cercle inscrits dans un octogone

De la troisième à la première L

constructions avec contraintes - octogone et arcs de cercle - copyright Patrice Debart 2008

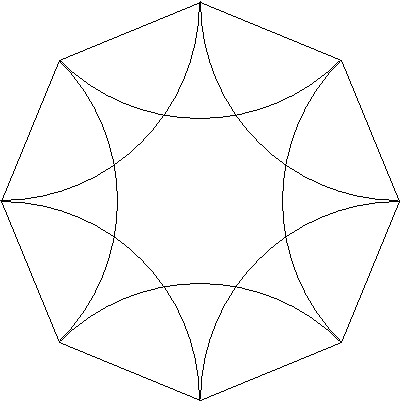
Reproduire la figure ci-contre, sachant que l'octogone est régulier et que les arcs de cercle sont tangents deux à deux.

Télécharger la figure GéoPlan octogone_arcs.g2w

Figure copiée dans octogone et arcs de cercle

4. Une fleur de six pétales en forme de losanges

Dessiner un flocon avec 6 parallélogrammes

constructions avec contraintes - fleur de six petales en forme de losange - copyright Patrice Debart 2008

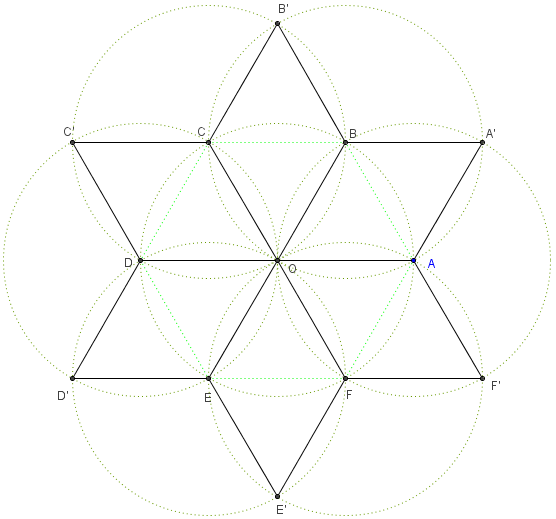
Tracer six losanges ayant un sommet au centre d'un hexagone régulier, avec pour diagonales les côtés de cet hexagone.

Figure interactive dans GeoGebraTube : fleur de 6 losanges

Figure copiée dans une fleur de 6 pétales en forme de losange

Il est possible de réaliser ces figures à partir de tout polygone régulier.

5. Recopier une figure : triangle curviligne

Dessiner une figure avec trois losanges d'angles 60°.

constructions avec contraintes - triangle curviligne - copyright Patrice Debart 2008

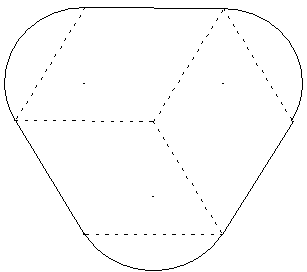
Réaliser cette figure sur une feuille, ou avec logiciel de géométrie dynamique, sachant que les arcs interceptent les côtés de trois triangles équilatéraux.

Télécharger la figure GéoPlan trois_arcs.g2w

Figure copiée par pinterest

6. Milieu d'une sécante

Classe de première L

Deux cercles

constructions avec contraintes - milieu d'une secante - copyright Patrice Debart 2008

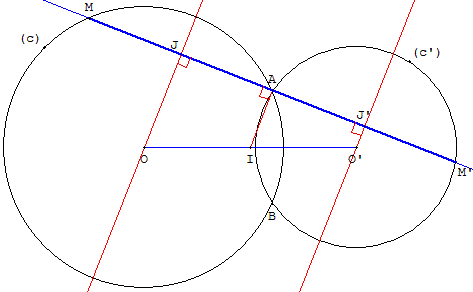
Soit deux cercles sécants en A ;

construire une sécante (MM’) aux deux cercles, passant par le point A, telle que A soit le milieu de [MM’].

Solution

I étant le milieu de la droite des centres [OO’], la sécante es la perpendiculaire en A à (IA).

Télécharger la figure GéoPlan milieu_secante.g2w

7. Corde et centre de gravité

Résolution de triangle

Classe de première L

constructions avec contraintes - corde et centre de gravite - copyright Patrice Debart 2008

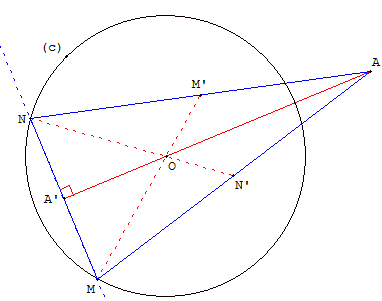
Étant donné un point A et un cercle (c) de centre O, construire un triangle AMN tel que M et N soient des points de (c) et que O soit le centre de gravité du triangle.

On pourra remarquer que le triangle cherché est isocèle (les médianes issues de M et N sont de même longueur, égale à du rayon du cercle).