Descartes et les Mathématiques

Problèmes de construction « à la règle et au compas »

Cycle III - Collège

Exercices de constructions géométriques au collège : triangles, carrés, trapèzes, cercles, tangentes…

Sommaire

Cycle III

    Construire un triangle connaissant les trois côtés, voir géométrie en cinquième

    Construire un carré connaissant deux sommets (consécutifs ou opposés), voir carré au collège

1. Dessiner un parallélogramme connaissant deux côtés non parallèles et d'une diagonale.

2. Dessiner un rectangle connaissant un côté et de la diagonale

6^e - 5^e

3. Dessiner un trapèze connaissant les quatre côtés

4. Dessiner un triangle connaissant un angle, un côté adjacent et la somme des deux autres

3^e Utilisation d'arcs capables

5. Dessiner un triangle connaissant un angle, la somme des côtés adjacents et le côté opposé

3^e Problèmes de contact

6. Dessiner un cercle tangent à trois cercles de même rayon

7. Dessiner un cercle tangent à deux cercles

8. Dessiner un cercle tangent à deux droites

9. Dessiner un cercle tangent à une droite et à un cercle

10. Dessiner les tangentes à deux cercles (sécants ou non)

11. Dessiner un cercle tangent à trois droites
      a. les trois droites sont deux à deux sécantes
      b. deux des trois droites sont parallèles

Construire un triangle connaissant deux sommets et le centre de gravité

Construire un cercle passant par trois points

1. Parallélogramme

Construire un parallélogramme ABCD connaissant les longueurs AB = a, BC = b de deux côtés consécutifs
et la longueur AC = d  d'une diagonale

Tracer un parallélogramme avec une diagonale.

Tracer un triangle ABC et compléter le parallélogramme avec le quatrième point D.

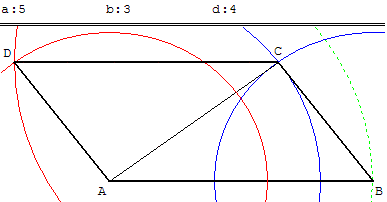
Placer un point A,
sur le cercle de centre A et de rayon a, placer un point B.

Tracer les cercles (c₁) de centre A, de rayon d et (c₂) de centre B de rayon b.

Si les cercles (c₁) et (c₂) sont sécants en C et C’, choisir C.

Compléter avec le point D : ici en continuant avec le compas, avec un des points d'intersection des cercles de centres A et C ; de rayons b et a.
Il est aussi possible d'utiliser la symétrie par rapport au milieu de [AC] ou encore la translation de vecteur .

2. Construire un rectangle

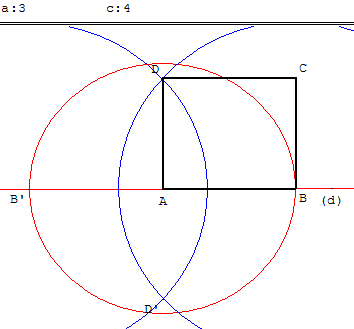
Comment tracer un rectangle avec un compas

Dessiner un rectangle ABCD connaissant la longueur AB = a d'un côté
et de la diagonale AC = c.

Indications

Placer un point A sur une droite (d),
Le cercle de centre A, de rayon a, rencontre (d) en B et B’.

Si c > a les cercles de centre B et B’ et de rayon c permette de Tracer la médiatrice (DD’) de [BB’].

Lorsque le point D existe, l'angle BÂD est droit.

Compléter le rectangle par le point C à l'aide, par exemple, de la translation de vecteur .

Télécharger la figure GéoPlan rectangle.g2w

3. Construction d'un trapèze

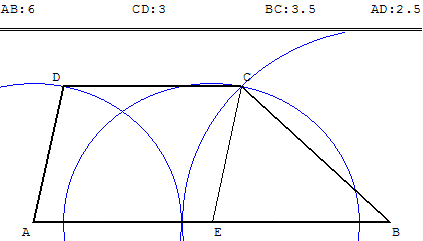
Construire un trapèze connaissant les longueurs des quatre côtés

AD = a = 2,5 ; D est sur le cercle c₁ de centre A et de rayon a.

Construction d'un trapèze de bases b et b’ et de côtés a et c :
AB = b = 6.
BC = c = 3,5 ; C est sur le cercle c₂ de centre B et de rayon c.
CD = b’ = 3 ; placer le point E sur [AB] tel que AE = b’.
Le point C est lui aussi sur le cercle (c₃) de centre E et de rayon a.
C est donc un des points d'intersection de (c₂) et de (c₃).
D est le quatrième point du parallélogramme AECD, image du point C par la translation de vecteur .

Télécharger la figure GéoPlan trapeze.g2w

4. Un triangle avec un angle, un côté et la somme des autres

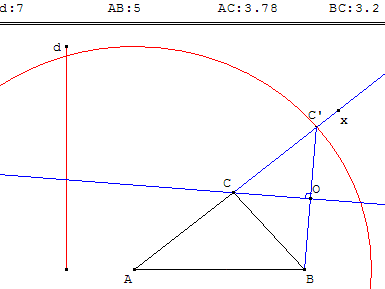
Construction d'un triangle connaissant un angle, un côté adjacent et la somme des deux autres

Tracer un triangle ABC connaissant l'angle BCA, la longueur c du côté AB et la somme d des côtés AC + BC.

  – l'angle BCA est donné par BAx. Avec GéoPlan, déplacer le « point noté x » pour modifier cet angle ;
  – la longueur c du côté adjacent AB est donnée : le point B variable sur la droite horizontale passant par A permet de faire varier cette longueur AB ;
  – la somme des côtés AC + BC est donnée par d, d > c. Avec GéoPlan, déplacer le « point d » pour modifier ce nombre.

Le cercle de centre A, de rayon d, rencontre la demi-droite [Ax) en C’.
La médiatrice de [BC’] rencontre [Ax) en C.
Le triangle ABC est solution

Voir: construire un triangle connaissant deux côtés et l'angle compris entre ces deux côtés

Voir aussi : construire un triangle rectangle connaissant l'hypoténuse c et la somme r des deux autres côtés de l'angle droit

Télécharger la figure GéoPlan tri_somme_cotes.g2w

5. Un triangle avec un angle, la somme des côtés et l'opposé

Construire un triangle connaissant un angle, la somme des côtés adjacents et le côté opposé.

Tracer un triangle ABC tel que :
  – le côté AB soit donné : le point B variable sur la droite horizontale passant par A permet de modifier la longueur AB ;
  – la somme des côtés AC + BC soit donnée par d, avec GéoPlan déplacer le «point d» pour faire varier ce nombre ;
  – et l'angle ACB soit égal à l'angle donné xÎy où (Ix) est parallèle à (AB). Avec GéoPlan, déplacer le « point y » pour modifier cet angle.

Le point C se trouve sur l'arc capable qui « voit » le segment [AB] sous un angle égal à xÎy.
Le centre J de cet arc se trouve à l'intersection de la médiatrice de [AB] et de la perpendiculaire à (Iy) passant par A.
En effet, l'angle AOJ est égal à xÎy, c'est la moitié de l'angle au centre AJB.

Le cercle de centre A et de rayon d recoupe la droite (AC) en C’.

La somme AC + BC est égale à AC₁ avec le point C₁ sur la droite (AC) tel que CC₁ = BC.
Le triangle BCC₁ est isocèle ; les angles CBC₁ et BC₁C sont égaux,
la somme des angles est CBC₁ + BC₁C + C₁CB = 180°, donc 2 BC₁C + C₁CB = 180°.
De l'angle plat ACB + BCC₁ = 180° on en déduit que ACB = 2 BC₁C = 2 AC₁B = xÎy.

C₁ est sur l'arc capable de centre M qui « voit » [AB] sous un angle égal à xÎy/2 ;
en effet : le point d'intersection M de la médiatrice de [AB] avec le cercle de centre J correspond à un angle inscrit AMB, égal à xÎy.
AMB est l'angle au centre associé à l'angle inscrit AC₁B. La médiatrice de [BC₁] passe par M.

Recherche

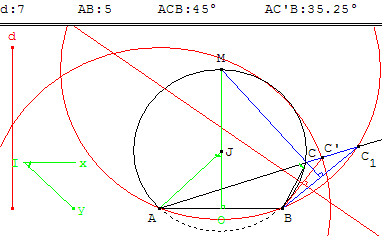
Une solution se trouve lorsque les points C’ et C₁ sont confondus à l'intersection du cercle de centre A et de rayon d et du cercle de centre M passant par A et B.

Déplacer C pour une recherche avec GéoPlan.

À partir d'une solution, on trouve les trois autres par symétries par rapport à la droite (AB) ou à la médiatrice de [AB].

Une des quatre solutions.

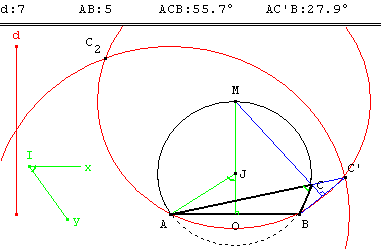
Technique GéoPlan

Pour tracer les deux solutions, correspondant aux points d'intersection C₁ ou C₂, des deux cercles utiliser des commandes d'affectations directes.

Réaliser la figure avec un point libre C’ :
Par simple appui sur la touche 1 l'affectation directe permet de donner la valeur de l'objet C₁ à l'objet libre C’ (point de même genre).
Cette affectation est provisoire puisque la variable C’ reste libre.
Par appui sur la touche 2 une autre affectation directe permet de donner la valeur du point C₂ au point libre C’.

Télécharger la figure GéoPlan tri_somme_cotes2.g2w, la figure GéoPlan tri_somme_cotes3.g2w

Problèmes de contact

6. Cercle tangent à trois cercles de même rayon

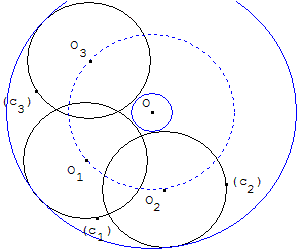
Constructions avec des cercles

Cas particulier du problème CCC des trois cercles d'Apollonius

Soit trois cercles c₁(O₁, r) ; c₂(O₂, r) et c₃(O₃, r) de même rayon.

Tracer le point O intersection des médiatrices du triangle O₁O₂O₃.
Le cercle (c₄) de centre O circonscrit au triangle O₁O₂O₃ a pour rayon OO₁ = r₄.

Le cercle de centre O et de rayon la somme r + r₄ est tangent à ces trois cercles et les contient tous les trois.

Si O est à l'extérieur des trois cercles, alors r₄ > r. Le cercle de centre O et de rayon la différence r₄ − r est tangent à ces trois cercles, à l'extérieur de tous les trois.

Télécharger la figure GéoPlan tg_3_cercle.g2w

7. Construire un cercle de rayon donné, tangent à deux cercles

Soit deux cercles c₁(O₁, r₁) et c₂(O₂, r₂).

Un cercle (c) de rayon r est tangent extérieurement à (c₁) si son centre est situé à une distance r + r₁ de O₁,
il est tangent intérieurement à (c₁) et (c) est à l'intérieur de (c₁) si r₁ > r et si son centre est situé à une distance r₁ − r de O₁,
enfin (c₁) est à l'intérieur de (c) si r > r₁ et le centre de (c) est situé à une distance r − r₁ de O₁.

De même, le cercle (c) est tangent à (c₂) si son centre est situé à une distance de O₂ égale selon les cas à r + r₂, r − r₂ ou r₂ − r.
Lorsque le problème admet une solution (c), le cercle (c’) symétrique par rapport à la ligne des centres (O₁O₂) s'en déduit immédiatement.
On trouvera 0, 2, 4, 6 ou 8 solutions illustrées par ces exemples.

Cercle tangent extérieurement

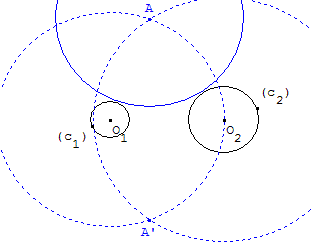
(c) tangent extérieurement à (c₁) et (c₂). Son centre A ou A’ est à l'intersection des cercles de centre O₁, de rayon r + r₁ et de centre O₂, de rayon r + r₂.

Cercle tangent intérieurement

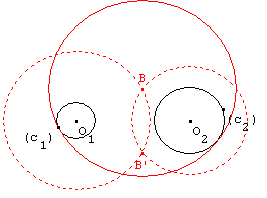
(c) tangent intérieurement à (c₁) et (c₂). Son centre B ou B’ est ici à l'intersection du cercle de centre O₁, de rayon r − r₁ et du cercle de centre O₂, de rayon r − r₂.

Cercle tangent intérieurement et extérieurement

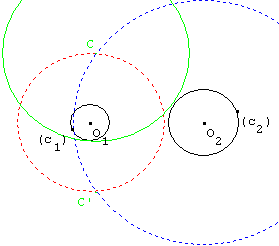
(c) de centre C, tangent intérieurement à (c₁) et extérieurement à (c₂).

Cercle tangent extérieurement et intérieurement

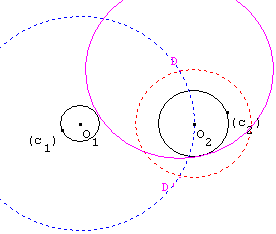
(c) de centre D tangent extérieurement à (c₁) et intérieurement à (c₂).

Télécharger la figure GéoPlan tg_2_cercle.g2w

Cercle passant par un point tangent à deux cercles : voir problème de contact PCC

8. Construire un cercle de rayon donné, tangent à deux droites

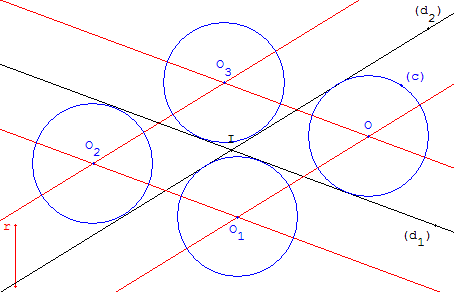
Cercles de rayon donné, tangents à deux droites données.

On donne deux droites (d₁ ), (d₂ ) sécantes, tracer les cercles de rayon donné, tangents à ces deux droites.

Indications

Le rayon r étant donné, construire les droites parallèles
à (d₁ ) et (d₂ ) situées à une distance r de ces deux droites.

Les parallèles construites forment un losange
de sommets O, O₁, O₂, O₃.

Les quatre cercles de rayon r, centrés aux sommets du losange, sont les solutions du problème.

Télécharger la figure GéoPlan cercle_tg_2_droites.g2w

9. Construire un cercle, tangent à une droite et à un cercle

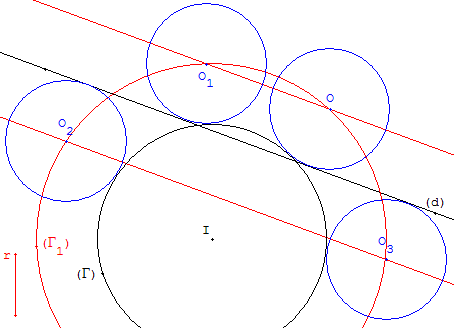
On donne une droite (d) et un cercle (Γ), construire les cercles de rayon donné, tangents à cette droite et à ce cercle.

Remarque

Le cercle (Γ) ayant pour centre I et pour rayon R, un cercle (c) de centre O et de rayon r est tangent extérieurement à (Γ) si IO = R + r, le point O est sur le cercle (Γ₁) de centre I et de rayon R + r.

Si R > r, le cercle (c) est tangent intérieurement à (Γ) si IO = R − r, le point O est sur le cercle (Γ₂) de centre I et de rayon R − r.

Indications

Le rayon r étant donné, tracer les deux droites parallèles à (d), situées à une distance r de cette droite.

Construire les points d'intersection de ces parallèles avec les cercles (Γ₁) et (Γ₂) de centre I et de rayons R + r et R − r.

Télécharger la figure GéoPlan cercle_r_tg_dr_ce.g2w

Cercles tangents extérieurement à (Γ) :

Tracer le cercle (Γ₁) de centre I et de rayon R + r.

Les points d'intersection de (Γ₁) et des parallèles, lorsqu'ils existent, sont les centres de cercles solutions.

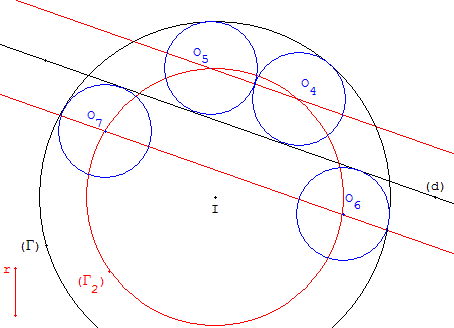
Cercles tangents intérieurement à (Γ) :

Si R > r, il est possible de tracer le cercle (Γ₂) de centre I et de rayon R − r.

Les points d'intersection de (Γ₂) et des parallèles, lorsqu'ils existent, sont les centres d'autres cercles solutions.

Résolution complète

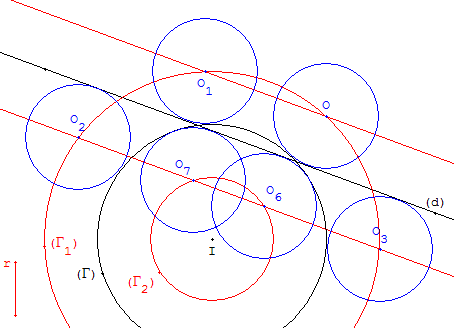
Au maximum huit solutions.

10. Tracer les tangentes à deux cercles (sécants ou non)

10.a. Cercles d'un même côté des tangentes communes

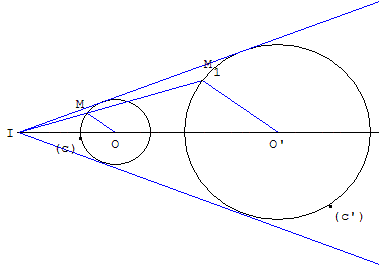
Soit deux cercles c(O, r) et c’(O’, r’) avec r < r’
le petit cercle (c) n'est pas à l'intérieur de (c’) : r + OO’ > r’.

Construire le point I, intersection de deux tangentes, situé sur la ligne des centres (OO’).
Pour le tracer il suffit, étant donné un point M variable sur (c), de trouver un point M₁ de (c’) tel que le rayon OM₁ soit parallèle à OM et de même sens. Le point I est l'intersection des droites (OO’) et (MM₁).

Par I, on peut mener deux tangentes communes aux deux cercles. Pour les tracer avec précision, on trouve les points de contact comme intersection du cercle (c) avec le cercle de diamètre [IO] ou comme intersection du cercle (c’) avec le cercle de diamètre [IO’].

Télécharger la figure GéoPlan homo_cercle.g2w

10.b. Quatre tangentes pour deux cercles non sécants

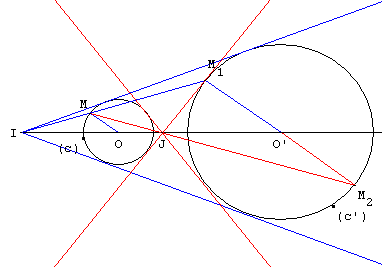
De même, si les cercles (c) et (c’) sont extérieurs l'un à l'autre (r + r’ < OO’), on trouve un deuxième point J en traçant le point M₂ de (c’), tel que le rayon OM₂ soit parallèle à OM et de sens contraire. L'intersection J des droites (OO’) et (MM₂) est alors le point de concours de deux autres tangentes. Tracer les points de contact de ces tangentes, par exemple comme intersection du cercle (c) avec le cercle de diamètre [OJ].

Paragraphe adapté pour le collège de la page homothéties

Voir aussi les constructions avec deux cercles auxiliaires : le cercle au collège

11. Construire un cercle tangent à trois droites

11.a. Cercle tangent à trois sécantes

Classe de quatrième
Droites remarquables d'un triangle
Bissectrices intérieures

Les trois bissectrices intérieures d'un triangle ABC sont concourantes en I.
Le point I est le centre du cercle inscrit dans le triangle ABC, tangent aux trois côtés de ce triangle.

Construction des bissectrices avec la géométrie dynamique

Il existe des commandes pour tracer la bissectrice d'un angle, le cercle inscrit et le centre de ce cercle.

Il est aussi possible de réaliser la « construction à la règle et au compas » comme suit :

Tracer la bissectrice de l'angle BAC en utilisant la configuration du losange :
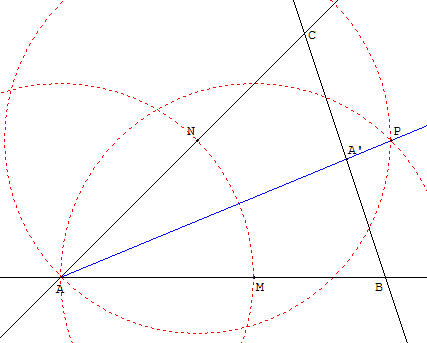
Placer un point M sur le côté (AB).
Tracer le cercle de centre A passant par M qui coupe le deuxième côté (AC) en N.
Tracer les deux cercles de centre M et N passant par A.
Ces deux cercles se recoupent en P.
La droite (AP) est la bissectrice cherchée.

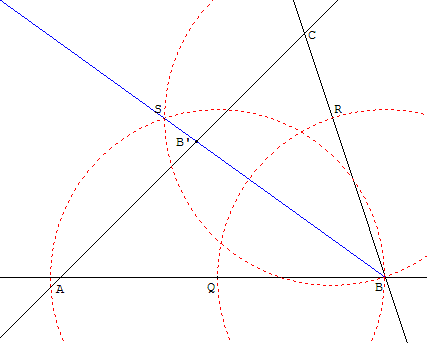
De même, tracer une deuxième bissectrice, celle de l'angle ABC.

La bissectrice (AS) coupe le côté [AC] en B’.

Cercle tangent à trois sécantes, deux à deux, non parallèles

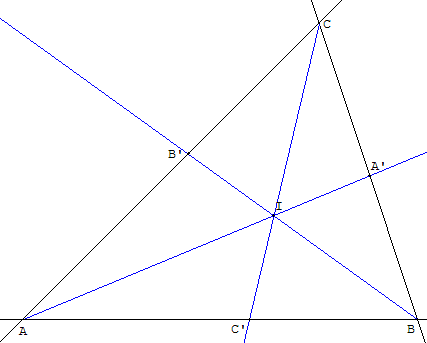
Ces deux bissectrices se coupent en I.
La droite (CI) est la troisième bissectrice.

Télécharger la figure GéoPlan bissectr.g2w

Problème de contact DDD : au lycée, on construira aussi les trois cercles exinscrits du triangle avec les bissectrices extérieures,

voir : géométrie du triangle

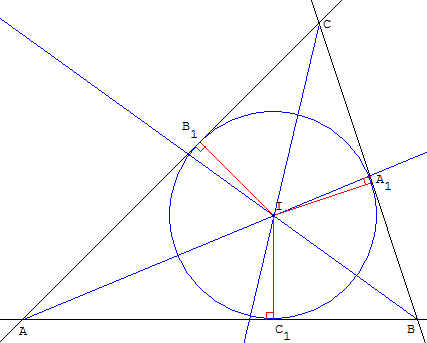
Par projection orthogonale du point I, par exemple sur le côté (AB),
on obtient un point C₁ qui permet de tracer le cercle inscrit.

GéoPlan permet de tracer directement ce cercle avec l'instruction :
« Créer>Ligne>Cercle>Cercle défini par centre et tangente ».

Scénario GéoPlan : taper C, A, A, B, B, C, D :

Charger la figure des trois bissectrices, taper C pour les effacer et retrouver uniquement le triangle ABC,
taper A pour tracer la bissectrice en A, retaper A pour l'effacer,
taper B pour tracer la bissectrice en B, retaper B pour l'effacer,
taper C pour retrouver les trois bissectrices,
terminer par D pour obtenir le cercle inscrit.

11.b. Cercle tangent à trois droites dont deux sont parallèles

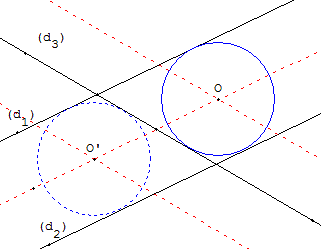
Le rayon r du cercle est égal à la moitié de la distance entre les deux parallèles (d₁) et (d₂).

Le centre du cercle se trouve sur la droite équidistante des deux parallèles et sur une des droites situées à une distance r de la sécante (d₃).

Il y a donc deux cercles solutions, centrés en O et O’.

Télécharger la figure GéoPlan cercle_tg_3droites.g2w