Descartes et les Mathématiques

Problèmes de contact : construction de cercles

Détermination de cercles astreints à trois conditions parmi : passer par un point ; être tangent à une droite ou tangent à un cercle.

0. Apollonius Gallus

La détermination de cercles astreints à trois conditions prises parmi celles qui consistent à passer par un point donné, ou à être tangent à une droite ou un cercle donné, répond à dix problèmes désignés par les symboles PPP, DDD, PPD, PPC… en représentant un point par P, une droite par D et un cercle par C. Ci-dessus est indiqué, pour chaque symbole, le nombre de solutions dont le problème est susceptible.

Le problème CCC, des trois cercles, dit problème d'Apollonius, est le plus difficile du traité des contacts, un des ouvrages perdus d'Apollonius.

Dans d’Apollonius Gallus, Viète va résoudre les dix problèmes de contact avec un enchaînement rappelant celui que nous présentons ci-dessous.

Le problème 1, PPP, est résolu avec le cercle circonscrit dont le centre est le point d'intersection des médiatrices du triangle.

Le problème 2, DDD, a pour solutions les cercles inscrit et exinscrits lorsque les droites forment un triangle. Viète le traitera de façon isolée.

Le problème 3, PPD, se ramène au problème 1 en utilisant des angles inscrits.

Le problème 4, PPC, se trouve grâce à l'introduction d'un cercle intermédiaire qui permet de trouver le point d'intersection des tangentes.

Le problème 5, PDD, se ramène au problème 4 en introduisant le symétrique du point par rapport à une bissectrice des deux droites.

Le problème 6, PCC, se ramène au problème 4 en trouvant un deuxième point situé sur la droite joignant le point donné à un des centres de similitude des deux cercles.

Le problème 7, PDC, se ramène au problème 3 grâce à un point intermédiaire.

Le problème 8, DDC, se ramène au problème 5 par la méthode des translations en déplaçant les droites d'une longueur égale au rayon du cercle.

Le problème 9, DCC, se ramène au problème 7 en remplaçant le plus grand des cercles par un cercle ayant pour rayon la somme ou la différence des rayons de ces deux cercles et l'on déplace la droite parallèlement à elle-même d'une longueur égale au rayon du petit cercle.

Le problème 10, CCC, se ramène au problème 6 en substituant aux deux plus grands cercles, des cercles concentriques dont les rayons différent d'une quantité égale au rayon du plus petit cercle.

1. Cercle passant par trois points

PPP : 1 solution

Paragraphe extrait de la page : la géométrie du triangle

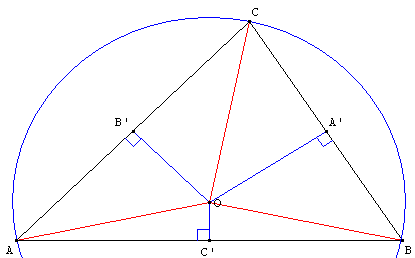
Déterminer les cercles passant par trois points distincts deux à deux.

Solution : le cercle circonscrit au triangle formé par les trois points.

La médiatrice d'un segment est la droite perpendiculaire au segment en son milieu. C'est l'ensemble des points équidistants des extrémités du segment.

Les trois médiatrices d'un triangle sont concourantes au même point, centre du cercle circonscrit au triangle.

Figure interactive dans GeoGebraTube : médiatrices d'un triangle

Feuille de travail avec GeoGebra

2. Cercle tangent à trois droites

DDD : 4 solutions

2.a. Cercle tangent à trois droites

Les trois droites sont sécantes deux à deux, non concourantes

Extrait de : la géométrie du triangle

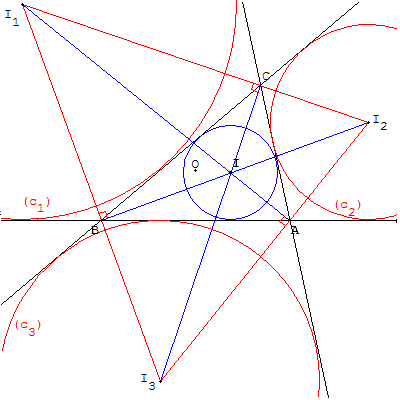
Étant donné trois droites se coupant en trois points distincts deux à deux, déterminer les cercles tangents à ces trois droites.

On trouve quatre solutions : tracer les bissectrices intérieures extérieures des angles formés par les trois droites.

Leurs points d'intersection sont les centres du cercle inscrit dans le triangle ABC et des trois cercles exinscrits.

Ces quatre cercles sont tangents aux côtés du triangle.

Figure interactive dans GeoGebraTube : cercles inscrit et exinscrits

Rappels de cours

La bissectrice d'un angle est la droite qui, passant par le sommet de cet angle, le partage en deux angles de même mesure.
Les trois bissectrices (intérieures) d'un triangle ABC sont concourantes en un même point I, centre du cercle inscrit dans le triangle (tangent intérieurement aux trois côtés du triangle).

Les bissectrices extérieures partagent en deux l'angle bordé par un côté du triangle et le prolongement de l'autre côté.
En un sommet, les bissectrices intérieure et extérieure sont orthogonales.

Deux bissectrices extérieures, associées à deux sommets, et la bissectrice intérieure, associée au troisième sommet, sont concourantes.

Leur point d'intersection situé à égale distance des trois côtés du triangle est le centre d'un cercle exinscrit, tangent aux trois côtés du triangle.

2.b. Cercle tangent à trois droites dont deux sont parallèles

Extrait de : problèmes de construction au collège

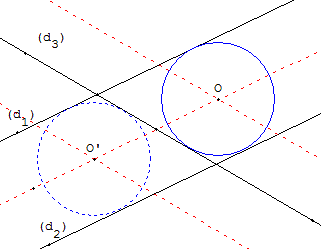
Le rayon r du cercle est égal à la moitié de la distance entre les deux parallèles (d₁) et (d₂).

Le centre du cercle se trouve sur la droite équidistante des deux parallèles et sur une des droites situées à une distance r de la sécante (d₃).

Il y a donc deux cercles solutions, centrés en O et O’.

Télécharger la figure GéoPlan cercle_tg_3droites.g2w

3. Cercle tangent à une droite passant par deux points

PPD : 2 solutions

Déterminer les cercles passant par deux points distincts A et B donnés et tangents à une droite (d) donnée.

Si A et B sont de part et d'autre de (d) il n'y a pas de solution.
Si A est sur (d) et B à l'extérieur il est immédiat de construire la solution dont le centre est à l'intersection de la médiatrice de [AB] avec la perpendiculaire en A à (d).
Si la droite (AB) est parallèle à (d) le point de contact est sur la médiatrice de [AB] et il n'y a qu'une solution.

Sinon on trouve deux cercles solutions que l'on détermine par leurs points de contact T et T’ avec la droite (d). Le centre d'un cercle solution est alors à l'intersection de la perpendiculaire à (d) au point de contact avec la médiatrice de [AB].

Si la droite (AB) est perpendiculaire à (d), il est facile de construire les cercles solutions de rayon égal à la distance de la médiatrice de [AB] à (d),
sinon trouver les points de contact des solutions et de (d), en traçant un cercle coupant (d) suivant les deux points de contact, avec une des deux constructions suivantes :

Angle inscrit dans un cercle

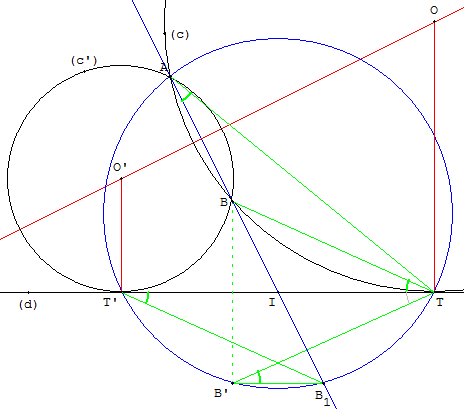
La droite (AB) rencontre (d) en I.
Placer le point B’ symétrique de B par rapport à (d) et le point B₁ le symétrique de B par rapport à I.
Tracer le cercle circonscrit à AB₁B’. Les points d'intersection T et T’ de la droite (d) avec ce cercle sont les points de contact de la droite (d) avec les deux cercles solutions de ce problème.

Preuve d'Emmanuel Moreau

En effet, dans le cercle circonscrit, les angles inscrits TAB₁ et TT’B₁ sont égaux.
Les angles IT’B₁ et BTI sont égaux par symétrie par rapport à I.
Dans le cercle circonscrit à ABT, l'angle inscrit TAB est donc égal à BTI.
L'angle inscrit interceptant l'arc BT est égal à l'angle de la corde (BT) et de la droite (d). Cette droite est bien la tangente au cercle qui est une des deux solutions cherchée.

Télécharger la figure GéoPlan cercle_PPD_2.g2w

GéoPlan permet de transformer cette construction en deux prototypes qui, à partir des points A et B et la droite (d), renvoient les cercles (c) ou (c’).

Télécharger les prototypes GéoPlan proto_PPD_2.g2w

Construction de Wallis

Construire les cercles solutions comme cercles du faisceau à points de base A et B : choisir un cercle particulier du faisceau comme celui de diamètre [AB].

Une tangente (IK) à ce cercle permet de tracer un deuxième cercle de centre I et de rayon IK. Ce deuxième cercle coupe la droite (d) en T et T’, points de contact des deux cercles solutions avec (d).

La justification se fait en utilisant la puissance du point I par rapport à ces cercles.

La puissance du point I, intersection de (AB) et de (d), par rapport à un cercle solution est IA × IB = IT². C'est aussi la puissance de I par rapport au cercle de diamètre [AB], puissance encore égale au carré de la longueur d'une tangente (IK) à ce cercle : IA × IB = IK².

IT et IK sont la moyenne géométrique entre IA et IB.

La construction de Wallis permet de construire une des tangentes en plaçant un point de contact K tel que la longueur IK soit égale à IT :

Pour cela, si J est le milieu de [AB], construire les cercles de diamètres [AB] et [IJ] qui se coupent en K. La droite (IK) est tangente au cercle de diamètre [AB] et  IK² est la puissance du point I par rapport aux cercles.

Le cercle de centre I, passant par K, rencontre (d) en T et T’, points de contact des deux solutions.

Télécharger la figure GéoPlan cercle_PPD.g2w

Remarque : dans la figure ci-contre à gauche, la puissance de I, par rapport au cercle circonscrit à AB₁B’,
est – IT × IT’ = – IA × IB = – IA × IB₁, ce qui justifie la construction du point B₁, puis de son symétrique B’ par rapport à la perpendiculaire à (d) en I.

Voir au collège, le cas particulier où un des points est situé sur la droite : cercle tangent à une droite en un point de cette droite, passant par un autre point extérieur à la droite

4. Cercle tangent à un cercle passant par deux points

PPC : 2 solutions

Déterminer les cercles passant par deux points distincts A et B donnés et tangents à un cercle (c) donné.

Principe

Construire le point I d'intersection de la droite (AB) avec les tangentes communes au cercle donné et aux cercles solutions.

Le point I a même puissance par rapport à (c) et à n'importe quel cercle (c₃) passant par A et B, il est donc sur l'axe radical de (c) et (c₃) {ensemble des points ayant même puissance par rapport aux deux cercles}.

Si (c₃) et (c) se coupent en C et D la droite (CD) est l'axe radical qui coupe (AB) au point fixe I.

Construction - Cas général

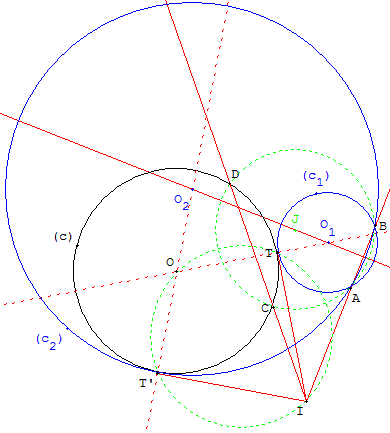
Étant donné un point C situé sur le cercle (c), le cercle (c₃) circonscrit au triangle ABC recoupe (c) en D.
Les droites (AB) et (CD) se coupent en I.

Soit T et T’ les points de contact des tangentes au cercle (c) issues de I, ces points T et T’ sont les intersections du cercle (c) avec le cercle de diamètre [IO],
où O est le centre du cercle (c).

La puissance du point I par rapport au cercle (c) est IC × ID = IT².

La puissance du point I par rapport au cercle (c₃) est IC × ID = IA × IB.

Soit (c₁) le cercle circonscrit au triangle ABT.
La puissance du point I par rapport au cercle (c₁) est IA × IB = IT².
La droite (IT) est tangente à (c₁) en T.
(c) et (c₁) sont tangents en T. Le cercle (c₁) est la première solution.

De même, le cercle (c₂), circonscrit au triangle ABT’, est tangent en T’ à (IT’) et à (c), c'est donc la deuxième solution du problème.

Cas particuliers

Si A et B sont équidistants de O, il y a encore deux solutions avec comme points de contact T et T’ intersections de (c) avec la médiatrice de [AB].

Si un des points est à l'intérieur du cercle (c), l'autre à l'extérieur, le point I intersection des droites (AB) et (CD) est situé à l'intérieur de (c), la puissance du point I par rapport à (c) est négative et il n'y a pas de solution.

Télécharger la figure GéoPlan cercle_PPC.g2w

Prototypes

GéoPlan permet de transformer cette construction en deux prototypes qui, à partir des points A et B et du cercle (c), renvoient les cercles (c₁) ou (c₂).

Télécharger les prototypes GéoPlan proto_PPC_2.g2w

5. Cercle tangent à deux droites passant par un point donné

PDD : 2 solutions

On donne deux droites (d₁), (d₂) sécantes en O et un point A n'appartenant pas à ces droites.
Existe-t-il un cercle (c) passant par A tangent à ces deux droites ?
Combien y a-t-il de solutions à ce problème ?

Solution

Cas général : A n'est pas équidistant de (d₁) et (d₂).

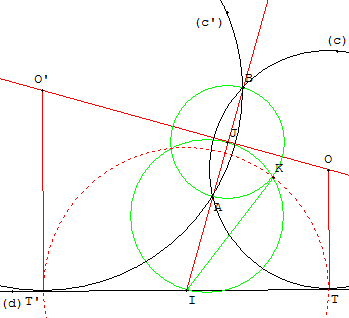
Un cercle solution (c) passe par le point A’ symétrique de A par rapport à la bissectrice de l'angle formé par (d₁, d₂) contenant le point A. On se trouve dans le cas PPD du problème 3 : tracer un cercle tangent à la droite (d₁) par exemple, passant par deux points A et A’ avec possibilité d'utiliser les prototypes GéoPlan.
I étant le point d'intersection de (AA’) avec (d₁), la construction de Wallis permet de placer un point K tel que la longueur IK soit égale à IT₁.

Pour cela, si J est le milieu de [AA’], construire les cercles de diamètres [AA’] et [IJ] qui se coupent en K. (IK) est tangente au cercle de diamètre [AA’] et  IK² est la puissance du point I par rapport aux cercles.

Le cercle de centre I, passant par K, rencontre (d₁) en T₁ et T₂, points de contact des deux solutions.

Les cercles circonscrits à AA’T₁ et AA’T₂, passant par A et A’, tangents à (d₁) et (d₂), sont les deux cercles (c₁) et (c₂) solutions du problème. Leurs centres O₁ et O₂ sont les intersections de la bissectrice avec les perpendiculaires à (d₁) en T₁ et T₂.

Télécharger la figure GéoPlan cercle_PDD.g2w

Cas particulier

Lorsque A est situé sur une des bissectrices de deux droites, I est l'intersection de (d₁) avec la perpendiculaire en A à (OA).
Le cercle de centre I, passant par A, rencontre (d₁) en T₁ et T₂, points de contact des deux solutions et IT₁ = IT₂ = IA.
Les centres O₁ et O₂ des deux cercles solutions sont les intersections de la bissectrice avec les perpendiculaires à (d₁) en T₁ et T₂.

Télécharger la figure GéoPlan cercle_PDD_2.g2w

Autre méthode : tracer un cercle tangent aux deux droites et construire les solutions par transformation :
voir au lycée : homothétie,

voir construction sans homothétie : cercle au collège

6. Cercle passant par un point tangent à deux cercles

PCC : 4 solutions

On donne deux cercles (c₁), (c₂) de centres O₁, O₂, de rayons r₁, r₂ et un point A n'appartenant pas à ces cercles.
Existe-t-il un cercle (c) passant par A tangent à ces deux cercles ?
Combien y a-t-il de solutions à ce problème ?

Recherche de centres d'homothétie

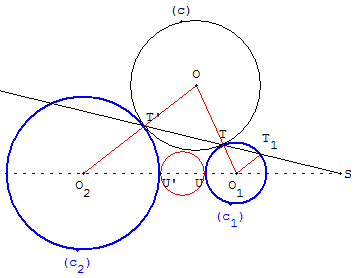
Si r₁= r₂ la translation de vecteur O₁O₂ et la symétrie de centre S’ milieu de [O₁O₂] transforme le cercle (c₁) en (c₂).

Si r₁ ≠ r₂ il existe deux homothéties H(S, r₁/r₂) et H(S’, – r₁/r₂) transformant (c₁) en (c₂).

Les points S et S’ centres d'homothétie des cercles sont les points qui partagent le segment [O₁O₂] dans le rapport r₁/r₂.

Si un cercle variable (c) est tangent aux cercles (c₁), (c₂) en T et T’, la droite (TT’) qui joint les points de contact passe par un centre d'homothétie. La puissance p du centre d'homothétie par rapport au cercle (c) variable est constante.

p = ST × ST’ = ST × ST₁ × ST’/ST₁ = ST × ST₁ × r₂/r₁.

On obtient la puissance du point S par rapport au cercle (c₁), multipliée par le rapport des rayons.

Si U et U’ sont les points d'intersection de (c₁) et (c₂) avec la ligne des centres, la puissance du point S par rapport au cercle de diamètre [UU’] permet de retrouver le nombre
p = SU × SU’.

Télécharger la figure GéoPlan similitude_CC.g2w

L'homothétie H(S, r₁/r₂) transforme T₁ en T’ et T en T₂. La transformation, qui à T fait correspondre T’, est l'inversion de pôle S, de puissance p.

Le cercle (c) est globalement invariant par cette inversion.
Dans cette page les inversions transformant (c₁) en (c₂) sont réduites à une construction où, à partir d'un point T sur (c₁), la droite (ST) coupe (c₂) en T’ et T₂. Si T₂ est l'homologue de T par l'homothétie, plaint T’ est l'inverse de T.
Le cercle (c) est globalement invariant par l'inversion.

Deux prototypes GéoPlan permettent d'automatiser la construction de T’ en fonction T :
T’ image de T dans l'inversion positive qui transforme (c₁) en (c₂).

De même, pour l'inversion de puissance négative de pôle S’ :
T’’ image de T dans l'inversion négative qui transforme (c₁) en (c₂).

Télécharger les prototypes GéoPlan inversion.g2w

Centre d'homothétie positive

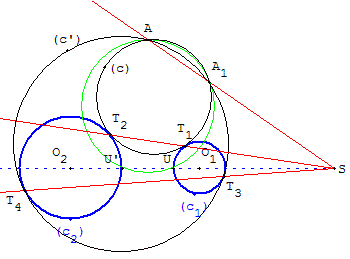
Le cercle (c) passe par le point A₁ de la droite (AS) tel que : p = SA × SA₁.

Or p = SU × SU’ donc U, U’, A et A₁ sont cocycliques. A₁ est le deuxième point d'intersection du cercle circonscrit au triangle AUU’ avec la droite (AS).

On est donc ramené au cas PPC du problème 4 : tracer un cercle passant par deux points A et A₁, tangent au cercle (c₁), avec possibilité d'utiliser les prototypes GéoPlan.

On a donc comme solutions un cercle (c) extérieur aux cercles (c₁), (c₂) et un cercle (c’) contenant les cercles (c₁), (c₂).

Télécharger la figure GéoPlan cercle_PCC.g2w

Inversion

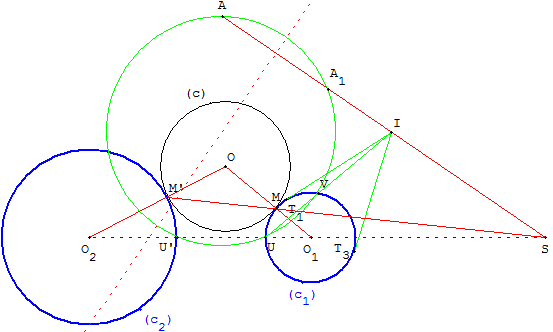
Si un cercle (c) de centre O est tangent en M et M’ à deux cercles (c₁) et (c₂), les points M et M’ sont homologues dans l'une des inversions transformant (c₁) en (c₂).

Le cercle (c) est globalement invariant par cette inversion.

Considérons l'inversion de pôle S et de puissance positive p = SU × SU’ transformant (c₁) en (c₂).
Le cercle circonscrit aux points U, U’ et A est globalement invariant par cette inversion. Le point A₁, image de A par l'inversion, est situé à l'intersection de ce cercle et de la droite (SA).

Le cercle (c) de centre O, intersection des droites (O₁M) et (O₂M’), est solution si le point O est situé sur la médiatrice de [AA₁]. Dans ce cas, la droite (MI) est la tangente commune.

Comme nous l'avons vu ci-dessus, le point I est l'intersection des droites (SA) et (UV) où U et V sont les points d'intersection du cercle (c₁) et du cercle circonscrit au triangle UU’A. Les points de contact T₁ et T₃ des tangentes à (c₁) issues de I donnent les solutions.

Télécharger la figure GéoPlan inversion_PCC.g2w

Centre d'homothétie négative : deux inversions

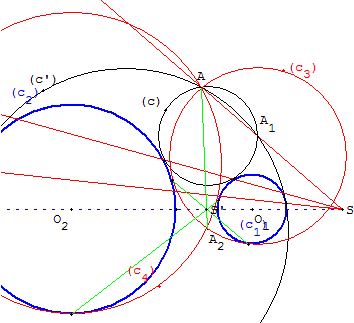
Lorsque les cercles (c₁) et (c₂) sont extérieurs l'un à l'autre, on a deux autres cercles solutions, invariants par homothétie de centre S’, de rapport négatif.

Le cercle passe par le point A₂ de la droite (AS’) tel que :
p = S’A × S’A₂.

Or p = S’U × S’U₂ donc U, U₂, A et A₂ sont cocycliques. A₂ est le deuxième point d'intersection du cercle circonscrit au triangle AUU₂ avec la droite (AS’).

On est donc ramené au cas PPC du problème 3 : tracer un cercle passant par deux points A et A₂, tangent au cercle (c₁).

On a donc comme solutions le cercle (c₃) extérieur à l'un des cercles
(c₁) ou (c₂) et extérieur à l'autre ; on a aussi le cercle (c₄) extérieur et intérieur étant inversés.

Télécharger la figure GéoPlan cercle_PCC_2.g2w

Exemple avec quatre inversions

Deux inversions positives et deux négatives

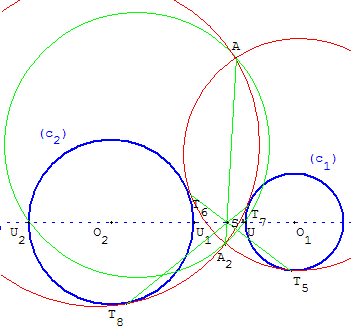
La droite (T₁T₂) des points de contact du cercle (c) passe par S,
ainsi que la droite (T₃T₄) des points de contact du cercle (c’).
Les points A et A₁ communs aux deux cercles sont alignés avec S.

Lorsqu'ils existent le segment [T₅T₆] des points de contact du cercle (c₃) passe par S’,
ainsi que le segment [T₇T₈] des points de contact du cercle (c₄).
Les points A et A₂, communs aux deux cercles, sont alignés avec S’.

Inversion :
A₂ est l'image de A par l'inversion de pôle S’ et de puissance négative :
p = − S’U × S’U’. Elle transforme T₅ en T₆ ; T₇ en T₈.

Télécharger la figure GéoPlan cercle_PCC_3.g2w

Voir aussi, la construction d'un cercle de rayon donné, tangent à deux cercles donnés : problème de construction

Centres des cercles tangents à deux cercles tangents donnés : voir lieux géométriques

Article exporté dans WikiPédia : Problèmes de contact

7. Cercle passant par un point tangent à une droite et à un cercle

PCD : 4 solutions

On donne une droite (d), un cercle (c) de centre O et un point A.
Soit I la projection orthogonale du centre O sur (d).

Les résultats du chapitre précédent subsistent, un des cercles étant remplacé par une droite :

Les centres d'homothétie étant remplacés par deux pôles d'inversion : les points U et U’, extrémités du diamètre de (c) perpendiculaire à (d), U’ étant le point le plus près de (d).

Cercles tangents extérieurement

Le point A₁ est alors l'image de A par l'inversion de pôle U, qui échange la droite et le cercle.

Plus simplement les résultats ci-dessus subsistent en plaçant A₁ deuxième point d'intersection du cercle circonscrit au triangle AIU’ avec la droite (AU).

On est donc ramené au cas PPD du problème 3 : tracer les cercles passant par deux points A et A₁, tangents à la droite (d).

Lorsque A et (d) sont à l'extérieur du cercle (c), A et (c) dans un même demi-plan par rapport à (d), on a deux cercles solutions, tangents extérieurement au cercle donné.

Pour chaque cercle les points de contact sont alignés avec le point U.

Lorsque la droite (d) et le cercle (c) sont sécants, appeler U le point du diamètre situé dans le même demi-plan que A par rapport à (d), on trouve alors deux solutions, quel que soit la position de A. Si A est à l'intérieur de (c), les deux cercles sont tangents intérieurement à (c).

Cercles tangents intérieurement

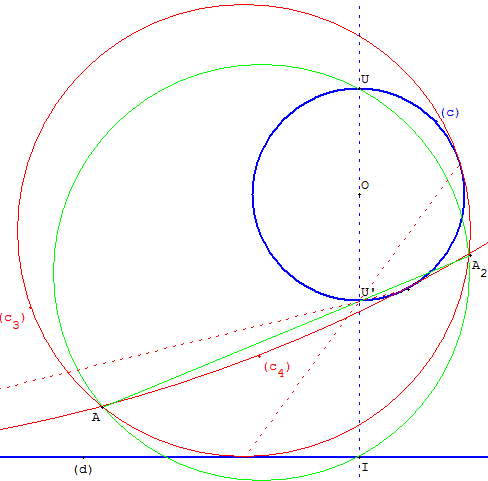
Le point A₂ est l'image de A par l'inversion de pôle U’, qui échange la droite et le cercle.

Le point A₂ est donc à l'intersection du cercle circonscrit au triangle AIU avec la droite (AU’).

Le problème devient : tracer les cercles tangents à la droite (d) (ou au cercle c), passant par deux points A et A₂

Lorsque (c) et (d) n'ont pas de point commun et si le point A est situé dans le même plan que le cercle (c) par rapport à la droite, il existe deux autres solutions où le cercle donné est à l'intérieur du cercle solution.

Pour chaque solution, le point U’ est sur le segment joignant les points de contact.

Télécharger la figure GéoPlan cercle_PDC.g2w

Cas particuliers : Point A sur le cercle

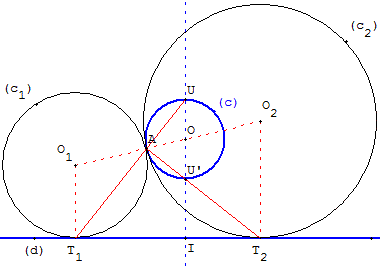
Lorsque le point A est sur le cercle, on trouve les points de contact comme intersection de la droite (d) et des droites (AU) et (AU’).
Si A est distinct des points U et U’, on trouve deux cercles dont les centres O₁ et O₂ sont les intersections des perpendiculaires à (d) aux points de contact avec la droite (AO).

Télécharger la figure GéoPlan cercle_PDC_3.g2w

Point A sur la droite

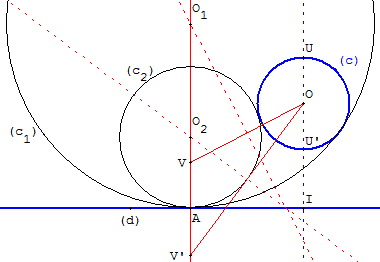
Si le point A est sur la droite (d), placer sur la perpendiculaire en A à (d) les points V et V’ situés à distance de A égale au rayon du cercle (c). Les centres O₁ et O₂ des cercles tangents sont les intersections de cette perpendiculaire avec les médiatrices de [OV] et de [OV’].

Télécharger la figure GéoPlan cercle_PDC_4.g2w

8. Cercle tangent à deux droites et à un cercle

DDC : 4 solutions

Ce problème a été résolu par Viète avec le recours à des droites et des cercles auxiliaires. Cette méthode sera nommée « méthode de Viète » ou des « translations parallèles ».

On donne deux droites (d₁), (d₂) sécantes en I et un cercle (c), de centre O, de rayon r.

Utiliser la « méthode des translations parallèles » en remarquant que si le rayon du cercle cherché augmentait ou diminuait de r, rayon du cercle donné, le nouveau cercle passerait par le centre O du cercle donné et serait tangent à des droites translatées de (d₁) et (d₂), telle que la distance entre une droite et son image soit égale au rayon r.
On se trouve dans le cas PDD du problème 5 : tracer un cercle tangent à deux droites passant par le centre O avec possibilité d'utiliser les prototypes GéoPlan.

Nous pouvons trouver jusqu'à quatre cercles centrés sur la bissectrice de l'angle formé par (d₁, d₂) contenant le point O.
Nous utiliserons le fait que si un cercle passe par O, il passe par O’ symétrique de O par rapport à la bissectrice et nous tracerons les cercles passant par O et O’ tangent aux parallèles à (d₁) (prototypes du chapitre 3).

Cercles tangents extérieurement

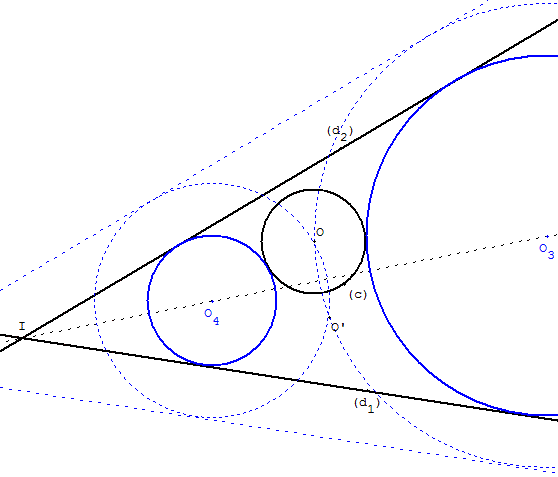
À partir des deux cercles de centres O₁, O₂, de rayons r₁, r₂,
nous trouvons les cercles (c₁), (c₂),
de rayons r₁+ r, r₂ + r.

Télécharger la figure GéoPlan cercle_DDC.g2w

Cercles tangents intérieurement

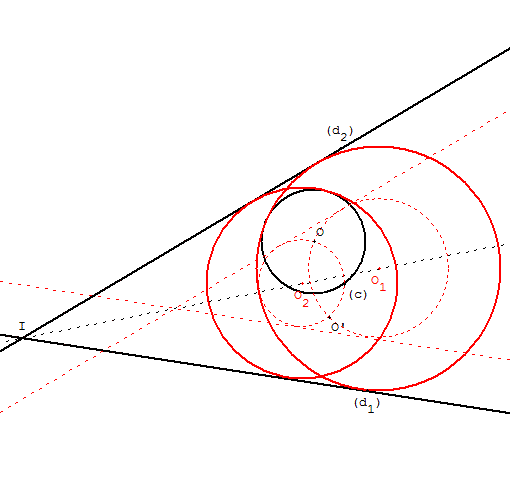
Lorsque le cercle (c) est entièrement contenu à l'intérieur du secteur angulaire,
à partir des deux cercles de centres O₁, O₂, passant par O et O’, de rayons q₁, q₂ nous trouvons les cercles (c₁), (c₂),
de rayons r₁= q₁+ r, r₂= q₂+ r tangents intérieurement à (c).

Cas particulier : point O situé sur la bissectrice

Télécharger la figure GéoPlan cercle_DDC_2.g2w

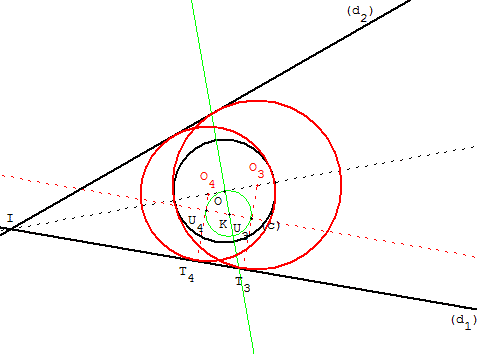
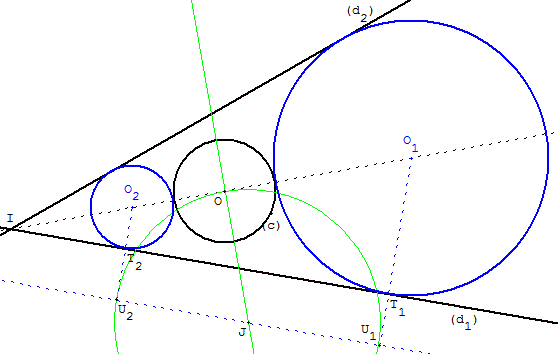
Lorsque le point O est situé sur la bissectrice, nous réalisons une construction de Wallis avec la perpendiculaire en O à la bissectrice de l'angle formé par (d₁, d₂), qui rencontre les translatées de (d₁) en J ou K

Le cercle de centre J, passant par O, rencontre la translatée en U₁ et U₂. Les perpendiculaires à (d₁) en U₁ et U₂ coupent la bissectrice au centres O₁ et O₂ et droite (d₁) aux points de contact T₁ et T₂ des deux cercles solutions.

Lorsque le cercle (c) est entièrement contenu à l'intérieur du secteur angulaire, le cercle de centre K, passant par O, rencontre la translatée en U₁ et U₂. Sur les perpendiculaires en U₃ et U₄, on trouve [O₃T₃] et [O₄T₄] qui sont les rayons de deux autres solutions.

9. Cercle tangent à une droite et à deux cercles

DCC : 8 solutions

On donne une droite (d) et deux cercles (c₁), (c₂) de centres O₁, O₂, de rayons r₁, r₂ tels que r₁ > r₂.

On remplace (c₁), le plus grand des deux cercles, par un cercle ayant pour rayon la somme r₁+ r₂ ou bien la différence r₁– r₂ des rayons
et on translate la droite (d) de telle façon que la distance entre la droite et son image soit égale à r₂, rayon du plus petit des cercles.

Avec la « méthode de Viète, des translations parallèles » et la « réduction du cercle (c₂) à un point », on se trouve dans le cas PCD du problème 7 : tracer un cercle passant par le point O₂, tangent à un cercle et à une droite.

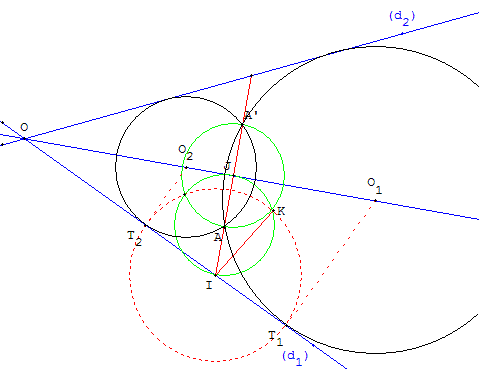
Le point O₁, se projette orthogonalement en H sur (d) (figures ci-dessous). Sur la droite (OH) soit [UU’] le diamètre du cercle de centre O₁ et de rayon r₁– r₂ et [U₁U₂] le diamètre du cercle de centre O₁ et de rayon r₁+ r₂. Soit I et I’ les points de (OH) situés à une distance r₂ et (d₁), (d₂) les translatées de (d) passant par I et I’.

On va examiner quatre configurations correspondant aux deux cercles de rayons r₁– r₂ et r₁+ r₂ associés aux droites (d₁), ou (d₂).

Télécharger la figure GéoPlan cercle_DCC.g2w

Selon la situation des cercles et de la droite, chaque configuration permet de trouver aucune, une ou deux solutions, ou huit solutions comme dans la figure ci-dessus.

Sangaku, nommé « Wasan »

Huit cercles tangents à (d ), (c₁) et (c₂)

Cercles (Γ₁) et (Γ₂) tangents extérieurement à (c₁) et (c₂)

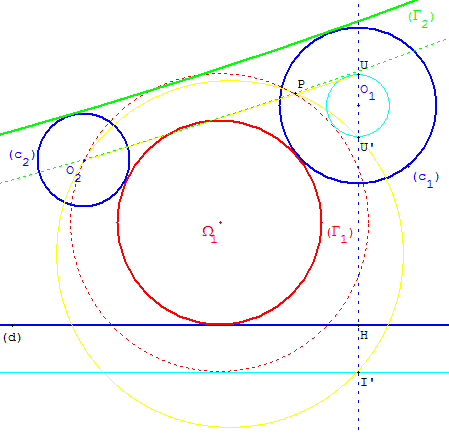
P est le deuxième point d'intersection du cercle circonscrit au triangle O₂I’U’ avec la droite (O₂U).
Lorsqu'il est possible, le tracé des cercles passant par O₂ et P tangents à (d₂) permet trouver jusqu'à deux cercles de centres Ω₁ et Ω₂, tangents au cercle de diamètre [UU’]. En diminuant les rayons de r₂ on obtient éventuellement deux solutions (Γ₁) et (Γ₂).

Télécharger la figure GéoPlan cercle_DCC_1.g2w

(c₁) et (c₂) tangents intérieurement à (Γ₅) et (Γ₆)

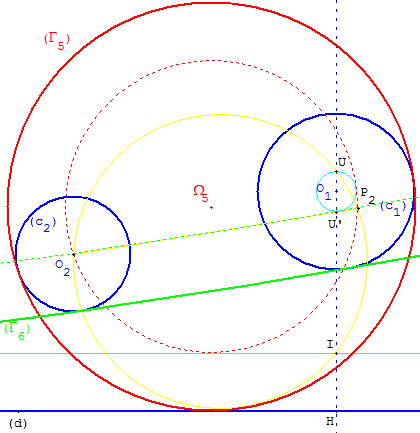
P₂ est le deuxième point d'intersection du cercle circonscrit au triangle O₂IU avec la droite (O₂U’).Il est encore possible (suivant les configurations), de tracer deux cercles passant par O₂ et P₂, tangents à (d₁) pour trouver jusqu'à deux cercles de centres Ω₅ et Ω₆, tangents au cercle de diamètre [UU’]. En augmentant les rayons de r₂ on obtient éventuellement deux autres solutions (Γ₅) et (Γ₆).

Télécharger la figure GéoPlan cercle_DCC_3.g2w

Γ₃ et Γ₄ tangents extérieurement à c₁, intérieurement à c₂

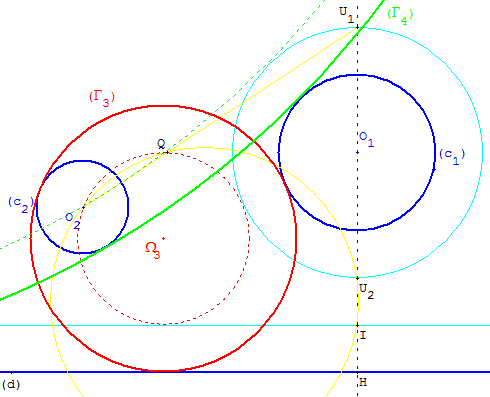
Q est le deuxième point d'intersection du cercle circonscrit au triangle O₂IU₂ avec la droite (O₂U₁).

Le tracé des cercles passant par O₂ et Q, tangents à (d₁), lorsqu'il est possible, permet trouver des cercles de centres Ω₃ et Ω₄, tangent au cercle de diamètre [U₁U₂]. En augmentant les rayons de r₂ on peut obtenir deux autres solutions (Γ₃) et (Γ₄).

Télécharger la figure GéoPlan cercle_DCC_2.g2w

Γ₇ et Γ₈ tangents intérieurement à c₁, extérieurement à c₂

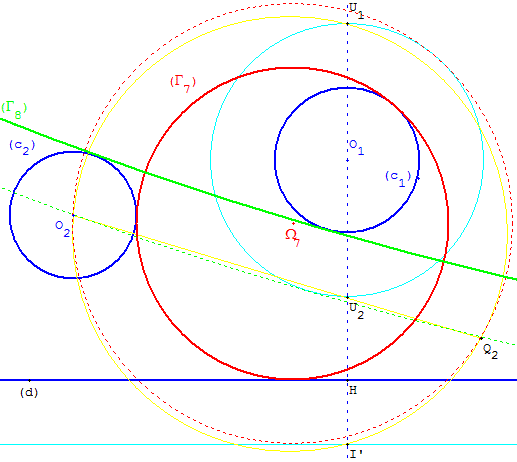
Q₂ est le deuxième point d'intersection du cercle circonscrit au triangle O₂I’U₁ avec la droite (O₂U₂).

Le tracé éventuel des cercles, passant par O₂ et Q₂, tangent à (d₂) permet de trouver jusqu'à deux cercles de centres Ω₇ et Ω₈, tangents au cercle de diamètre [U₁U₂].

En diminuant les rayons de r₂ on obtient les deux dernières solutions (Γ₇) et (Γ₈).

Télécharger la figure GéoPlan cercle_DCC_4.g2w

10. Un problème d'Apollonius : cercle tangent à trois cercles

CCC : 8 solutions

Problème des trois cercles

Trouver un cercle tangent à trois cercles donnés.

Historique

Le problème du cercle tangent à trois cercles est un des grands problèmes de l'histoire de la géométrie.
Il a été présenté par Pappus comme étant le dixième et le plus difficile du Traité des contacts, un des ouvrages perdus d'Apollonius.

En 1596, Adrien Romain (Van Roomen, latinisé en Adrianus Romanus, mathématicien flamand 1561-1615) proposera une solution faisant appel à une hyperbole, ce que Viète considère comme non conforme à la méthode des Anciens.

En effet, l'émergence de l'algèbre dans la géométrie lui permet d'affirmer que c'est un problème du second degré, donc un problème plan qui peut se résoudre « à la règle et au compas ».

Viète publie sa propre solution en 1600, dans l'Apollonius Gallus où il présente quelques lemmes permettant de manipuler les similitudes et où il expose les neuf premières situations présentées ci-dessus. Il reconnaît que les solutions de ce dixième problème dépendent de la position relative des trois cercles, mais ignore la discussion du nombre de solutions et il faudra attendre Descartes (1637) pour traiter les cas particuliers.

Jusqu'au  XIX^e siècle, ce problème sera un des lieux de la confrontation entre la géométrie synthétique (géométrie pure) et la géométrie analytique.

Circle tangent to three circles

Version anglaise sur Mathematics Stack Exchange

Méthode de Viète

C'est le principe de « réduction d'un cercle à un point », où l'homothétie (qui ne serra d'actualité qu'au XVIII^e avec Chasles) permet de transformer la contrainte « tangent à un cercle » en « passant par un point ».

On donne trois cercles (c₁), (c₂), (c₃) de centres O₁, O₂, O₃ de rayons r₁, r₂, r₃ tels que r₁ > r₂ > r₃ (Viète suppose implicitement que les trois cercles sont de rayons différents, les points O₁, O₂, O₃ n'étant pas alignés).

On substituera aux deux plus grands cercles (c₁), (c₂) des circonférences concentriques dont les rayons différeront des leurs d'une quantité égale au rayon r₃ du plus petit des trois cercles donnés.
On se trouve dans le cas PCC du problème 6 :
tracer un cercle tangent à deux cercles de centres O₁, O₂ passant par le centre O₃ du dernier cercle, que l'on ramène au cas PPC du problème 4  : tracer un cercle passant par O₃ et A (ou B) et tangent à un des cercles auxiliaires.

Un exemple avec huit solutions

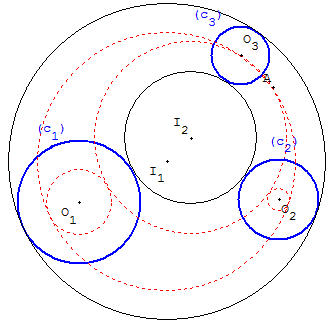
Sangaku : trois cercles tangents dans un cercle

Méthode de Viète en diminuant les rayons de r₃.

Cercles auxiliaires de centres O₁, O₂, de rayons r₁– r₃, r₂– r₃.

Télécharger la figure GéoPlan cercle_CCC_4.g2w

Méthode de Viète en augmentant les rayons

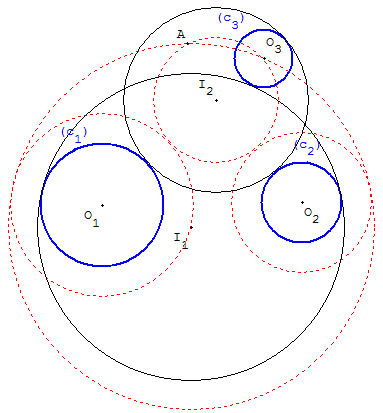
Cercles auxiliaires de centres O₁, O₂,
de rayons r₁ + r₃, r₂ + r₃.

Télécharger la figure GéoPlan cercle_CCC_3.g2w

Méthode de Viète en augmentant un rayon et en diminuant l'autre

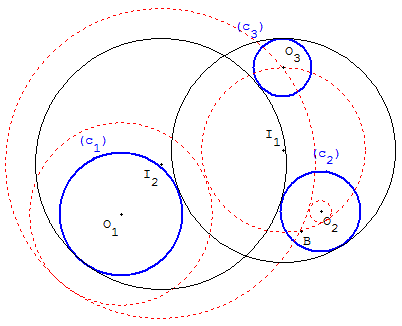
Cercles auxiliaires de centres O₁, O₂,
de rayons r₁ + r₃, r₂ – r₃.

Télécharger la figure GéoPlan cercle_CCC_5.g2w

Méthode de Viète en diminuant un rayon et en augmentant l'autre

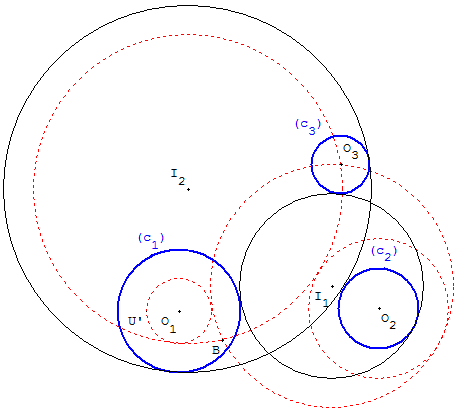
Cercles auxiliaires de centres O₁, O₂,
de rayons r₁ – r₃, r₂ + r₃.

Télécharger la figure GéoPlan cercle_CCC_6.g2w

Méthode des inversions

Théorème de D'Alembert
(ne pas confondre avec le théorème de D'Alembert-Gauss)

In F. G.-M. (Frère gabriel-Marie) -
Éléments de géométrie - 1877 - Gabay 2009

Trois cercles inégaux deux à deux et dont les centres ne sont pas alignés admettent six centres d'homothétie.
Les trois centres « positifs » S₁, S₂ et S₃ sont alignés. Deux centres « négatifs » sont alignés avec un centre « positif ».

Autrement dit, les six centres sont les sommets d'un quadrilatère complet.
Ce sont aussi des pôles d'inversion.

Solution du problème d'Apollonius

Construction de M. Fouché 1892

Ci-contre, une première figure permettant d'étudier les inversions i₁ et i₂ de puissances positives de pôles et S₂ et S₁. L'inversion i₁ échange les cercles (c₃) et (c₁), et l'inversion i₂ échange les cercles (c₃) et (c₂).

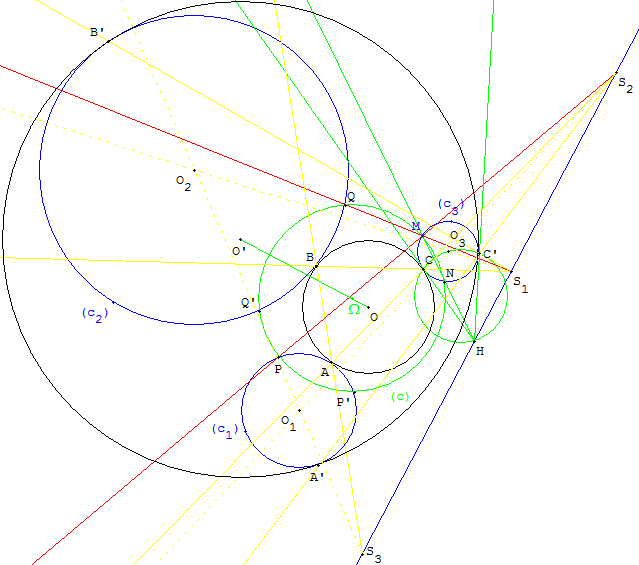
Étant donné un point M variable sur le cercle (c₃) construisons, lorsque c'est possible, les inverses P et Q de ce point M.
Pour l'inversion i₁, P est une des intersections bien choisie de (c₁) avec (S₂M).
Pour l'inversion i₂, Q est l'intersection de (c₂) avec (S₁M).

Le cercle (c), circonscrit au triangle MPQ, recoupe (c₃) en N.
Par l'inversion i₁, N a pour image P’, deuxième point d'intersection des cercles (c) et (c₁).
Par l'inversion i₂, N a pour image N’, deuxième point d'intersection des cercles (c) et (c₂).

En déplaçant le point M, on trouve une première position limite où les points M et N sont confondus en C. Les points Q et Q’ sont alors confondus en B, les points P et P’ sont aussi confondus en A. Le cercle (c) a pour position limite le cercle circonscrit à ABC coupant les trois cercles en trois points doubles, donc tangent aux trois cercles.
Une deuxième position limite est obtenue avec M et N confondus en C’, d'où Q et Q’ confondus en B’, et P et P’ sont confondus en A’. Cette position limite de (c) est le cercle circonscrit à A’B’C’, deuxième cercle tangent aux trois cercles.

La droite (MN) est l'axe radical de ce cercle circonscrit (c) et de (c₃). L'axe (MN) coupe la ligne (S₁S₂) des centres d'homothétie en H.
Le point H est indépendant du point M, la puissance du point H par rapport à (c₃) est aussi celle par rapport à un cercle solution.
La tangente commune au cercle solution et à (c₃) passe par H.

Il suffit de trouver les points de tangence C et C’ intersections de (c₃) avec le cercle de diamètre [O₃H].

En traçant le point A inverse de C, intersection de (c₁) avec (S₂C), puis en traçant le point B inverse de C, intersection de (c₂) avec (S₁C), on trouve une première solution : le cercle circonscrit à ABC.
De même avec A’, intersection de (c₁) avec (S₂C’), et B’ intersection de (c₂) avec (S₁C’), on trouve le cercle circonscrit à A’B’C’, comme deuxième solution.

Télécharger la figure GéoPlan cercle_CCC.g2w

Voir : discussion géométrie

Inversions de puissances de signes opposés

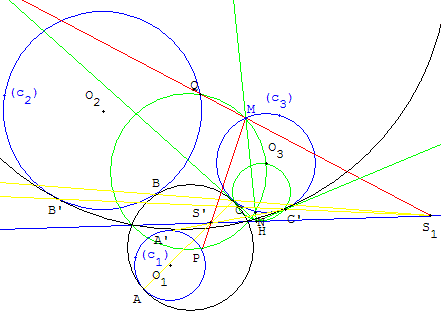
L'inversion de pôle S’, de puissance négative, échangeant les cercles (c₃) et (c₁) ainsi que l'inversion de pôle S₁, de puissance positive, échangeant les cercles (c₃) et (c₂) permettent d'obtenir deux autres solutions.

En permutant les cercles (c₁) et (c₂) cette figure permet d'obtenir l'inversion « positive » de pôle S₂ et l'inversion « négative » échangeant les cercles (c₃) et (c₂).

Télécharger la figure GéoPlan cercle_CCC_1.g2w

Applications : cercle et point d'Apollonius d'un triangle

théorème de Descartes - cercles de Soddy

Cas particulier : construction d'un cercle tangent à trois cercles de même rayon, voir : problème de construction

Inversions de puissances négatives

En général, on trouve huit solutions correspondant à ces quatre cas de figure.

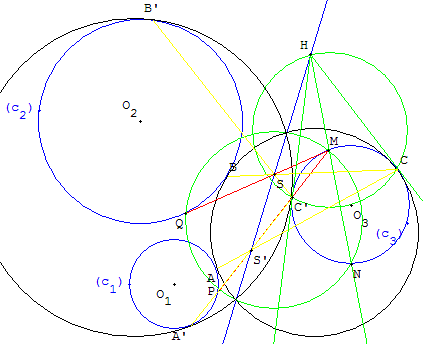
Pour chaque couple (c), (c’) de cercles solutions, de centres O, O’, la droite (OO’) est perpendiculaire à la ligne des centres d'homothétie correspondants.
Le centre Ω du cercle circonscrit à MPQ est situé sur droite (OO’).

Le point H a même puissance par rapport aux cercles (c), (c’), (MPQ). Ces cercles appartiennent au même faisceau ayant comme axe radical la ligne des centres d'homothétie. Dans les trois derniers cas, ces trois cercles sont sécants et les deux points de base sont situés sur la ligne des centres d'homothétie correspondants.

Télécharger la figure GéoPlan cercle_CCC_2.g2w