Descartes et les Mathématiques

Triangles rectangles

Configuration du plan : droites remarquables du triangle rectangle - Exemples d'exercices pouvant être résolus, en classe de seconde,

Sommaire

1. Angle inscrit dans un demi-cercle

2. Théorème de Pythagore

3. Relations métriques dans le triangle rectangle

4. Construire un triangle rectangle

5. Cercle inscrit - Distances entre les sommets et les points de contact
    Trois cercles inscrits
    Somme des rayons des trois cercles inscrits
6. Droites remarquables du triangle rectangle

7. Droites des milieux

8. Médiane et hauteur

9. Moyenne proportionnelle

Sur tablette numérique ou smartphone, bascule automatique vers la version mobile

II. Résolution d'un triangle rectangle

Construire un triangle rectangle connaissant :
a. un angle aigu et le rayon du cercle inscrit

b. l'hypoténuse et la somme des côtés de l'angle droit

c. la médiane et la hauteur relative à l'hypoténuse

Dans d'autres pages du site

Construction connaissant un côté et la différence des deux autres : calcul de Mons. des Cartes

Inscription d'un triangle dans un demi-cercle

Cercles tangents du triangle rectangle

Propriétés du triangle rectangle - Définitions

Un des angles est droit, les deux autres angles sont aigus et complémentaires.
Le plus grand côté est l'hypoténuse : c'est le côté opposé à l'angle droit.
Les petits côtés adjacents à l'angle droit sont appelés cathètes.

Configurations fondamentales

Pour les triangles rectangles, il s'agit de savoir mettre en œuvre :
  – les propriétés des droites remarquables,

  – la droite des milieux et le théorème de Thalès,

  – les propriétés des angles et des aires des triangles,

  – les propriétés des triangles rectangles et l'inscription dans un demi-cercle.

En seconde la difficulté des raisonnements vient souvent de l'enchaînement de deux propriétés remarquables.

Triangles rectangles particuliers

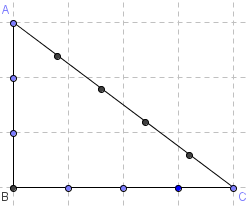
« Triangle égyptien » ou « triangle des arpenteurs »

Le triangle de côtés (3, 4, 5), connu depuis l'Antiquité, est rectangle d'après la réciproque du théorème de Pythagore.
Avec une corde à 13 nœuds ou « corde égyptienne », les Anciens s'en servaient comme équerre, entre autres, pour reconstituer les champs après les crues du Nil.

Figure interactive dans GeoGebraTube : triangle égyptien

« Demi-carré »

C'est le triangle rectangle isocèle d'angles aigus de 45°,
de côtés (1, 1, ), obtenu en divisant un carré en deux suivant une diagonale, d'où le nom du triangle.

« Triangle de l'écolier »

Triangle rectangle d'angles aigus de 30° et 60°

figure interactive dans GeoGebraTube : triangle de l'écolier

1. Angle inscrit dans un demi-cercle

1.a. Théorème dû à Thalès sur le cercle

Un angle inscrit dans un demi-cercle, chacun des côtés passant par une des extrémités du demi-cercle, est droit.

Un triangle inscrit dans un demi-cercle (un côté étant le diamètre) est un triangle rectangle.
Le demi-cercle, dont le diamètre est l'hypoténuse du triangle rectangle, est le cercle de Thalès du triangle rectangle.

Un triangle est rectangle si, et seulement si, le centre de son cercle circonscrit est le milieu d'un de ses côtés (ce côté est alors son hypoténuse).

Théorème de la médiane pour le triangle rectangle

Dans un triangle rectangle, la longueur de la médiane relative à l'hypoténuse est égale à la moitié de la longueur de l'hypoténuse.
Réciproquement : si dans un triangle la longueur d'une médiane est égale à la moitié de la longueur du côté correspondant, le triangle est rectangle.

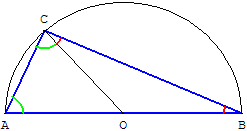
ABC est un triangle inscrit dans un demi-cercle de centre O.

1.b. Démonstration de Thalès

Deux côtés du triangle OAC sont des rayons, OAC est isocèle et les angles en A et C sont égaux : OÂC = ACO.
De même, OCB est isocèle et OBC = OCB.

En sommant ces deux égalités d'angles, il vient : OÂC + OBC = ACO + OCB = ACB.

Comme la somme des angles d'un triangle vaut 180°, il vient pour les angles du triangle ABC :
(OÂC + OBC) + ACB = 2 ACB = 180°.

Puis en divisant par 2, on obtient ACB = 90°.
Le triangle est donc bien rectangle en C.

Démonstration de la réciproque − Droites des milieux

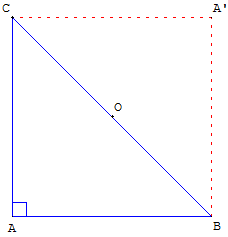
Si ABC est un triangle rectangle en C alors il s'inscrit dans un cercle de diamètre [AB]

On trace la droite des milieux passant par le milieu O de [AB] et le milieu B’ de [AC].
Elle est parallèle à (BC). Comme (BC) et (AC) sont perpendiculaires, il en est de même de (OB’) et (AC). (OB’) est donc la droite perpendiculaire à [AC] passant par le milieu de [AC], c'est la médiatrice de [AC].

De même, on démontre que la droite passant par O et par A’, milieu de [BC], est la médiatrice de [BC].
Ces deux médiatrices se coupent en O, milieu de [AB], qui est donc le centre du cercle circonscrit au triangle.
Le cercle circonscrit a bien pour diamètre [AB].

Comment tracer les médiatrices d'un triangle rectangle

Soit ABC un triangle rectangle en C, d'hypoténuse [AB] de milieu O.
Une des médiatrices est la perpendiculaire en O à (AB). On a vu ci-dessus que les deux autres médiatrices sont les droites des milieux [OA’] et [OB’].

1.c. Réciproque du théorème de Thalès sur le cercle

Un triangle rectangle est inscrit dans un demi-cercle.

Ci-dessous, deux démonstration de cette réciproque par doublement du triangle rectangle ABC par symétrie.

Pour cela, montrer que la médiane issue de l'angle droit est égal à la moitié de l'hypoténuse [AB] : le sommet C de l'angle droit est alors sur le cercle de diamètre [AB].

Le triangle rectangle est la moitié d'un rectangle

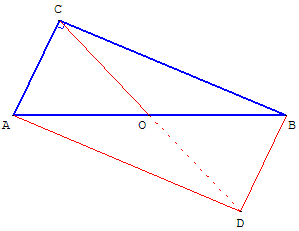
Soit D le point symétrique de C par rapport au point O, milieu de [AB].

Les deux triangles rectangles ABC et ABD forment un rectangle ACBD ;
en effet, les diagonales sont de même longueur et se coupent en leur milieu :
CO = CD = AB.

Calcul de l'aire du triangle rectangle

Le rectangle ACBD a une aire double de celle du triangle rectangle ACB.

2 Aire(ACB) = Aire(ACBD) = CB × CA = ab.

Aire(ACB) = ab.

L'aire d'un triangle rectangle est égale à la moitié du produit des côtés de l'angle droit.

Voir calcul avec hauteur et hypoténuse

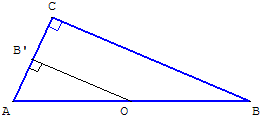
Le triangle rectangle est la moitié d'un triangle isocèle

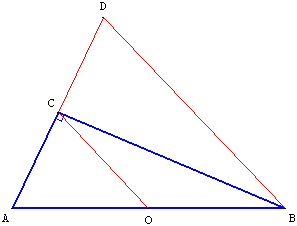
Soit le point D, symétrique de A par rapport au point C.

ABD est un triangle isocèle de médiatrice (CB).
C est le milieu de [AD] et (OC) est une droite des milieux :
CO = DB = AB.

2. Théorème de Pythagore

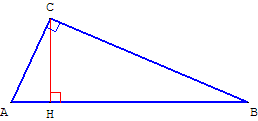
Dans tout triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des côtés de l'angle droit, et réciproquement.

Le théorème de Pythagore est très populaire et tout le monde se rappelle du « carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés » : c² = a² + b².

Preuve utilisant la méthode des aires grâce à la similitude du grand triangle rectangle ABC, rectangle en C, avec les triangles rectangles ACH et BCH formés par les petits côtés et la hauteur (CH), abaissée sur l'hypoténuse :

L'aire du grand triangle rectangle est la somme des aires des deux petits. Pour des triangles rectangles semblables, leurs aires sont proportionnelles aux carrés de leurs hypoténuses, donc le carré de l'hypoténuse du grand triangle est égal à la somme des carrés des hypoténuses des deux petits.

Télécharger la figure GéoPlan tr_rect.g2w

Comment trouver la hauteur d un triangle rectangle

Hauteur du triangle rectangle issue de l'angle droit

Le triangle rectangle ABC, rectangle en C, a pour hauteur issue de C, la droite (CH), perpendiculaire à l'hypoténuse [AB].

Comme tout triangle, le triangle rectangle a trois hauteurs :
outre la hauteur issue de l'angle droit, les deux autres hauteurs, issues des sommets des angles aigus, sont confondues avec les côtés de l'angle droit.

Le sommet C de l'angle droit, point de concours des trois hauteurs, est l'orthocentre du triangle rectangle.

3. Relations métriques dans le triangle rectangle

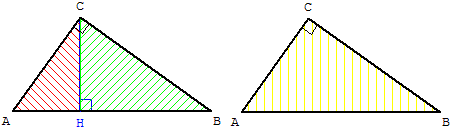
Triangles rectangles semblables

Les calculs dans le triangle rectangle utilisent la similitude des trois triangles rectangles CAB, HAC et HCB.

Télécharger la figure GéoPlan tr_rect_hauteur.g2w

3.a. Carré de la hauteur relative à l'hypoténuse

Théorème de la hauteur relative à l'hypoténuse

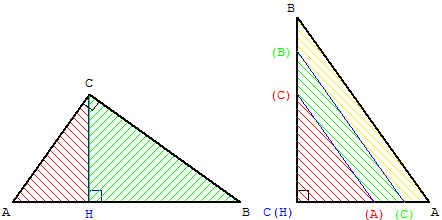
Soit [CH] la hauteur, issue du sommet de l'angle droit, du triangle rectangle ABC.
De la similitude des triangles rectangles BCH et CAH, en étudiant les rapports des petits côtés, on trouve :
HC/HA = HB/HC d'où HC² = HA × HB.

En 1^ère S, on vérifie cette relation avec le produit scalaire . = 0 ou
( + ).( + ) = ² + . = 0.

Énoncé du Théorème de la hauteur

ou théorème de Thalès suisse

HC² = HA × HB.

La hauteur issue de l'angle droit est la moyenne géométrique entre les projections des petits côtés sur l'hypoténuse.

Réciproque : si H est entre A et B et HC² = HA × HB alors le triangle ABC est rectangle en C.

Remarque : cette formule, due à Euclide, était connue de Descartes qui l'utilise, dans le premier livre de La Géométrie, pour calculer une racine carrée.

3.b. Premier théorème d'Euclide

Cathète : côté de l'angle droit d'un triangle rectangle.

Ancien synonyme de ligne perpendiculaire : droite qui tombe perpendiculairement sur une autre droite ou sur une surface.

Théorème des projections sur l'hypoténuse : carré d'un petit côté d'un triangle rectangle

Un côté de l'angle droit (cathète) est moyenne géométrique entre l'hypoténuse et sa projection sur l'hypoténuse.

AC² = AB × AH et BC² = BA × BH.

Démonstration de la relation BC² = BA × BH :
    – en 1^ère S grâce au produit scalaire :
avec la projection de A sur (BC) on a . = ² et avec la projection de C sur (AB) on a . = . ;
d'où . = BC² = BH × BA.

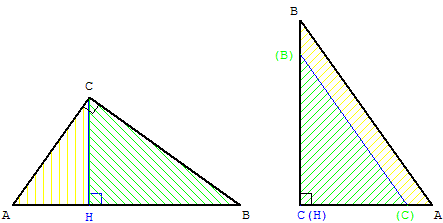
    – en classe de seconde avec la similitude des triangles rectangles ABC et CBH donne :

BC/BH = BA/BC d'où BC² = BA × BH (autre première moyenne proportionnelle).

Télécharger la figure GéoPlan tr_rect_metri2.g2w

Réciproque : si H est entre A et B et BC² = BH × BA alors le triangle ABC est rectangle en C.

Démonstration de la relationAC² = AB × AH :
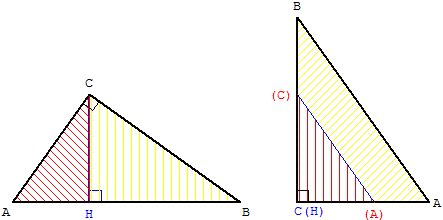De la similitude des triangles ABC et ACH on a :

AC/AB = AH/AC d'où AC² = AB × AH (première moyenne proportionnelle).

CH/BC = AB/AC d'où AC × BC = AB × CH (calcul de l'aire ci-dessous).

Télécharger la figure GéoPlan tr_rect_metri1.g2w

Mémorisation des formules

Il y a trois formules de moyennes géométriques dans le triangle ABC rectangle en C, de hauteur [CH] :

AC² = AB × AH,
BC² = BA × BH,
HC² = HA × HB (Théorème de la hauteur relative à l'hypoténuse).

Le point C mis à part, nous choisissons arbitrairement un des points A, B ou H et nous le plaçons en tête de chacun des trois termes qui interviennent. Il ne reste plus qu'à compléter avec les deux autres points restants.

Théorème des cathètes

Aire du triangle rectangle

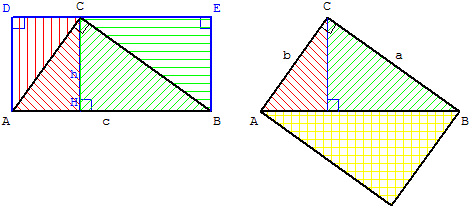
Le calcul de l'aire du triangle rectangle ABC, rectangle en C, avec les hauteurs se fait de deux façons et on a :

    – formule avec l'hypoténuse et la hauteur de l'angle droit :

Aire(ABC) = AB × CH = ch

    – et formule avec les côtés de l'angle droit :

Aire(ABC) = CA × CB = ba.

D'où le théorème des cathètes :

ba = ch, soit CA × CB = AB × CH : dans un triangle rectangle, le produit des cathètes est égal au produit de l'hypoténuse par la hauteur issue du sommet de l'angle droit.

Cette formule permet de calculer la hauteur du triangle rectangle : h = ba/c.

Télécharger la figure GéoPlan aire_tr_rect4.g2w
Retrouver ces calculs : aire du triangle

Quotient des carrés des petits côtés :

Calcul de l'inverse du carré de la hauteur CH

Des expressions du double de l'aire CH × AB = CA × CB, on trouve CH² = et avec Pythagore AB² = CA² + CB², en calculant l'inverse,
on a : .

Relations trigonométriques

sin  = ; cos  = sin = ; tan  = = ; sin²Â + cos²Â = 1.

Hauteur du triangle rectangle

CH = AC sin  ; AC = AB sin d'où CH = AB sin  sin = AB sin  cos Â.

Si h = CH et AB = c alors h = c sin  cos Â.

3.c. Calculer les côtés du triangle rectangle

Calculer la longueur d'un côté connaissant l'hypoténuse et l'autre côté

Utiliser la réciproque du théorème de Pythagore a² = c² - b².

Calculer la longueur d'un côté connaissant l'hypoténuse et un angle

Utiliser les relations trigonométriques
b = AC = AB sin = c sin ou AC = AB cos  = c cos Â.

Calculer la longueur d'un côté connaissant l'hypoténuse et la projection sur l'hypoténuse

Utiliser le théorème d'Euclide AC² = AB × AH.

3.d. Calculer l'hypoténuse du triangle rectangle

Calculer la longueur l'hypoténuse connaissant les deux autres côtés

Utiliser le théorème de Pythagore c² = a² + b².

Calculer l'hypoténuse connaissant un petit côté et un angle

Utiliser les relations trigonométriques c = AB = AC / sin ou AB = AC / cos Â.

4. Comment dessiner un triangle rectangle ?

Les figures n'ont pas encore été transférées de l'ancien site Orange

4.a. Comment tracer un triangle rectangle à partir d'un petit côté ?

Placer deux points A, B et tracer le segment [AB],
tracer la perpendiculaire à [AB] passant par B,
placer un point C sur la perpendiculaire
    (menu GéoPlan : créer > point > point libre > sur une droite).

Gommer la perpendiculaire (avec GéoPlan : non dessiné),
tracer les segments [BC] et [AC].

Marquer le milieu de [AB] et tracer le cercle de centre O, passant par A.

4.b. Comment dessiner un triangle rectangle à partir de l'hypoténuse ?

Placer deux points A, C, dessiner le segment [AC] et marquer le milieu O,
dessiner le cercle de diamètre [AC],
placer un point B sur le cercle (menu : créer > point > point libre >sur un cercle).
Tracer les segments [AB] et [BC],
gommer le cercle et le milieu de [AC] (non dessiné).

5. Cercle inscrit dans un triangle rectangle

5.a. Théorème japonais de Carnot dans le triangle rectangle

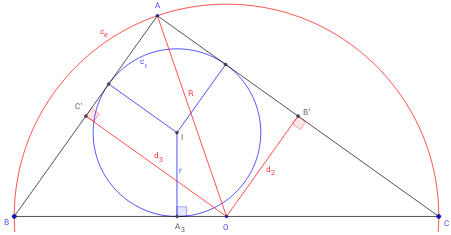
ABC est un triangle rectangle en A, C_e son cercle circonscrit de diamètre [AB], de centre O et de rayon R = BC/2 et C_i son cercle inscrit de centre I et de rayon r.
Les projetés orthogonaux de O sur les côtés [AC] et [AB] sont les milieux B' et C'.
Les distances du centre O aux petits côtés du triangle, notées par d₂ et d₃ sont OB' = AB/2 et OC' = AC/2.
La somme des distances du centre O aux côtés du triangle est donnée par :

AB + AC = BC + 2r ou b + c = a + 2r.

En effet, d'après le théorème général, la somme des distances du centre O aux côtés du triangle est :

d₂ + d₃ = R + r,

soit AB/2 + AC/2 = BC/2 + r, d'où la conclusion en multipliant par 2.

Figure interactive dans GeoGebraTube : théorème japonais de Carnot dans le triangle rectangle

Ci-dessous une aute façon de trouver ces résultats.

5.b.Distances entre les sommets et les points de contact

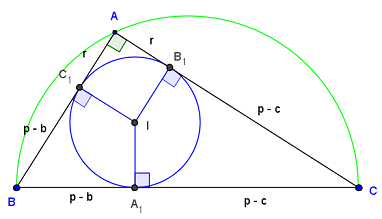
Points de contact du cercle inscrit avec les côtés du triangle rectangle

Soit l'hypoténuse BC = a ; AC = b et AB = c les côtés de l'angle de l'angle droit ;
p = (a + b + c) le demi-périmètre du triangle ABC et r le rayon du cercle inscrit.

Les trois bissectrices du triangle sont concourantes en I, centre du cercle inscrit dans le triangle (tangent intérieurement aux trois côtés du triangle).

Distance du sommet de l'angle droit aux points de contact :

r = AB₁ = AC₁ = p – a = (– a + b + c).

Le rayon du cercle inscrit est égal au demi-périmètre moins l'hypoténuse.

Les deux autres formules sont les mêmes que pour un triangle quelconque :
BA₁ = BC₁ = p – b = (a – b + c),
ainsi que CA₁ = CB₁ = p – c = (a + b – c).

Figure interactive dans GeoGebraTube : cercle inscrit dans un triangle rectangle

Application : un calcul de l'aire du triangle rectangle ABC

BA₁ × CA₁ = ( p – b)(p – c) = (a – b + c) × (a + b – c) = (a² – b² – c² + 2bc) = bc = S,
car la relation de Pythagore donne a² – b² – c² = 0.

Le produit des segments déterminés par le cercle inscrit sur l'hypoténuse est égal à l'aire du triangle.

Comme dans tout triangle, la formule des aires donne pour l'aire S du triangle rectangle ABC : S = pr, d'où r = = .

5.c. Trois cercles inscrits dans le triangle rectangle

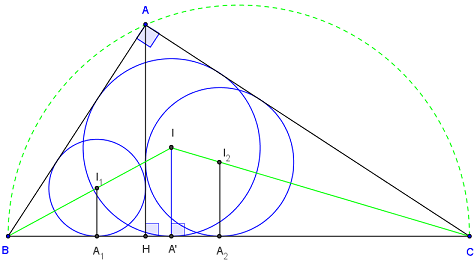
et les deux autres triangles rectangles formés avec la hauteur

Proportionnalité des rayons de cercles inscrits

Soit r le rayon du cercle inscrit dans le triangle rectangle ABC et h la hauteur AH ;
r₁ celui du cercle inscrit dans le triangle HBA, r₂ celui du cercle inscrit dans le triangle HAC.

Grâce à la similitude des triangles rectangles ABC, HBA et HAC,
on vérifie que les rayons r, r₁ et r₂ sont liés par les relations :

r/a = r₁/c = r₂/b,

Les rayons des cercles inscrits sont proportionnels aux hypoténuses des triangles rectangles semblables ABC, HBA et HAC.

On peut aussi faire intervenir la hauteur h :

r/c = r₁/h et r/b = r₂/h.

Par ailleurs, le théorème de Pythagore généralisé permet de déduire la relation :

r² = r₁² + r₂².

Figure interactive dans GeoGebraTube : trois cercles inscrits du triangle rectangle

5.d. Somme des rayons de trois cercles inscrits

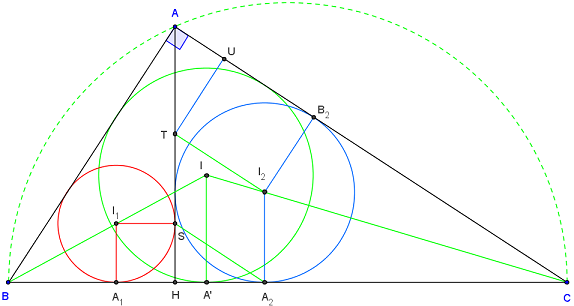
et les deux triangles rectangles formés avec la hauteur

La hauteur AH est égale à la somme des rayons des trois cercles inscrits dans les triangles rectangles ABC, ABH et ACH.

On a :

h = r + r₁ + r₂.

La vérification par le calcul se fait en additionnant les trois formules :
r = (– a + b + c), r₁ = ( h + BH – c)
et r₂ = (h + HC – b).

Figure interactive dans GeoGebraTube : rayonsde cercles inscrits du triangle rectangle

Démonstration géométrique

SH = r₁,
le triangle rectangle HSA₂, ayant des petits côtés de longueurs r₁ et r₂, est semblable à ABC.
L'hypoténuse SA₂mesure r.

La parallèle à (SA₂) passant par I₂ coupe (AH) en T. SA₂I₂T est un parallélogramme et ST = r₂.

Soit U la projection de T sur (AC). Le triangle rectangle UAT est semblable à ABC (mêmes angles, car un côté commun et les deux autres côtés sont perpendiculaires deux à deux).
UT = r₂, donc les triangles UAT et HSA₂ sont isométriques et TA = r.

On a bien HA = HS + ST + TA = r₁ + r₂ + r.

Après le bac, lire la suite sur la page point de Feuerbach dans le triangle rectangle

6. Droites remarquables d'un triangle rectangle

ABC est un triangle rectangle en C, inscrit dans le demi-cercle de centre O, de diamètre [AB].

6.a Bissectrices

La bissectrice de ce triangle, issue de A, rencontre en D le demi-cercle.
Les bissectrices du triangle rectangle sont concourantes en I, centre du cercle inscrit dans le triangle.

BDI rectangle isocèle

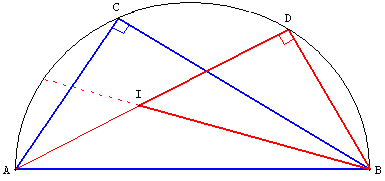
En étudiant les angles de la figure, montrer que le triangle BDI est rectangle isocèle.

Indications

Le triangle ABD, inscrit dans le demi-cercle est rectangle en D, d'où l'angle BDI est droit.

Les angles aigus du triangle rectangle ABC sont complémentaires,
donc CAB + ABC = 90°.
Les bissectrices partagent ces angles en deux,
d'où, en divisant par 2, on a IAB + ABI = 45°.

L'angle extérieur DIB du triangle ABI est égal à la somme de deux angles IAB + ABI,
soit DIB = 45°.

Le triangle rectangle BDI, ayant un angle de 45°, est rectangle isocèle.

Télécharger la figure GéoPlan tr_rect_bissect_2.g2w

6.b. Médiatrice de [BC]

Montrer que (OD) est la médiatrice de [BC].

Indications

Soit J le milieu de [BC], la médiatrice de [BC] est la droite des milieux (OJ) du triangle ABC.

La bissectrice (AD) partage l'arc BC en deux parties égales, donc les arcs DB et DC sont de même longueur et DB =DC. DBC est isocèle et D, comme O, est situé sur la médiatrice de [BC].

Autre démonstration : AOD est un triangle isocèle de côté le rayon du demi-cercle. Les angles égaux sont alors la moitié de l'angle BAC. Les angles alternes-internes DAC et ADO sont égaux à cette moitié, d'où la droite (OD) est parallèle à (AC).
Elle donc perpendiculaire à (BC) et passe par les milieux.
C'est encore la médiatrice de [BC].

Troisième démonstration : en étudiant les angles de la figure, montrer que le triangle CDI est isocèle (angles égaux à la moitié de BAC + 45°) et conclure avec le triangle rectangle isocèle BDI.

6.c. Médiane

Théorème de la médiane pour un triangle rectangle

Dans un triangle rectangle, la longueur de la médiane issue du sommet de l'angle droit vaut la moitié de la longueur de l'hypoténuse.

Réciproque du théorème de la médiane

Si dans un triangle, la longueur de la médiane issue d'un sommet vaut la moitié de la longueur du côté opposé, alors ce triangle est rectangle en ce sommet.

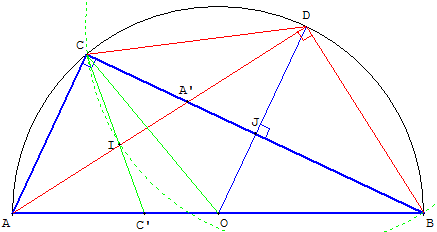
7. Droites des milieux du triangle rectangle

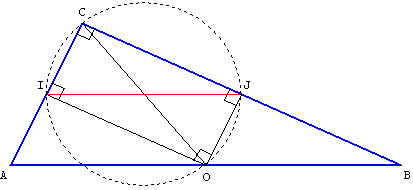
ABC est un triangle rectangle en C et O est le milieu de l'hypoténuse [AB].
Le cercle de diamètre [CO] coupe le côté [AC] en I et [BC] en J.

Quelle est la nature du quadrilatère OICJ ?
Que représentent I et J pour les côtés [AC] et [BC] ?

Justifier l'égalité des angles BAC et CÔJ, de même l'égalité des angles ABC et CÔI.

8. Médiane et hauteur d'un triangle rectangle

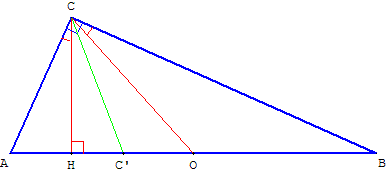
ABC est un triangle rectangle en C et O est le milieu de l'hypoténuse [AB].

(CH) est la hauteur issue de C.

Montrer, en étudiant les angles aigus des triangles ACH et BOC, que les angles ACB et HCO ont même bissectrice, la droite (CC’), bissectrice de l'angle droit.

La hauteur (CH) est aussi la symédiane en C, du triangle ABC.

9. Moyenne proportionnelle dans un triangle rectangle

9.a.Les Éléments d'Euclide - Livre VI - Proposition 13

Le terme « droite » désigne, dans les éléments d'Euclide, ce que nous appelons « segment ».

9.b. Trouver une moyenne proportionnelle

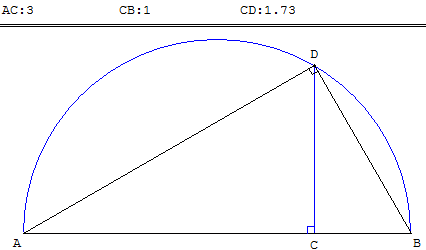
Méthode reprise par Descartes

Soit AC, et CB deux droites données ; il faut trouver une moyenne proportionnelle entre AC et CB.

Plaçons ces deux droites dans la même direction (AB), et sur laquelle décrivons le demi-cercle ADB. Du point C levons la perpendiculaire CD à AC qui rencontre la circonférence en D et joignons AD, DC.

L'angle ADB est inscrit dans un demi-cercle, cet angle est droit. Et puisque dans le triangle rectangle ADB on a mené, de l'angle droit, la droite DB perpendiculaire à la base, la droite DB est br entre les segments AB, BC de la base.

Donc, les deux droites AC, CB étant données, on a trouvé une moyenne proportionnelle DC, ce qu'il fallait faire.

Construction de réels

Application : La quadrature du rectangle, Éléments d'Euclide, livre II, proposition 14, voir constructions géométriques au collège

Deux autres méthodes

Lorsque les nombres a et b sont grands, à partir d'un point I, placer deux points A et B tel que IA = a et IB = b.
Utiliser une des deux constructions suivantes :

9.b. Carré d'un petit côté

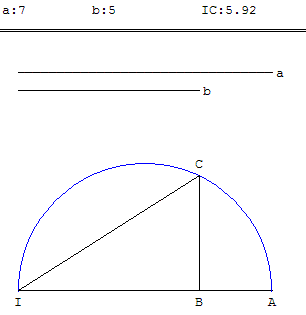
Tracer un demi-cercle de diamètre IA (a>b). La perpendiculaire en B à (IA) coupe ce demi-cercle en C.

Un côté de l'angle droit du triangle rectangle ICA est moyenne proportionnelle entre l'hypoténuse IA et sa projection sur l'hypoténuse IB : IA × IB = IC².
IC est la moyenne géométrique de a et b.

9.c. Construction de Wallis

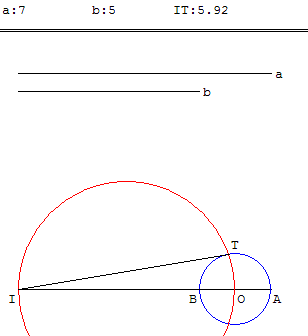
La puissance d'un point I par rapport à un cercle passant par A et B est le produit IA × IB. Cette puissance est égale au carré de la longueur IT d'une tangente au cercle, issue de I : IA × IB = IT².
IT est la moyenne géométrique de a et b.

En choisissant le cercle de diamètre [AB] de centre O, T est alors un des points d'intersection avec le cercle de diamètre [IO].

Télécharger la figure GéoPlan moy_geo2.g2w

II. Résolution de triangles rectangles

Comment résoudre un triangle rectangle

II.a. Un angle aigu et le rayon du cercle inscrit

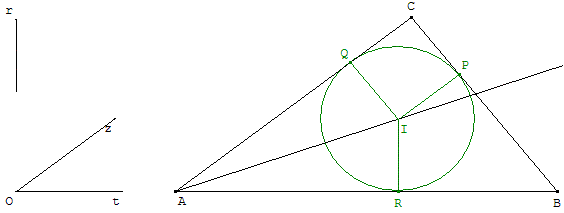
Tracer un triangle rectangle connaissant un angle aigu et le rayon du cercle inscrit

Le triangle ABC rectangle en C a un angle aigu A égal à tÔz.
Construire la droite passant par A parallèle à la bissectrice de tÔz.

Indications

La parallèle à (At) située à une distance r coupe cette bissectrice en I. Le point I se projette en R sur (At).
Le cercle inscrit est le cercle de centre I, passant par R.

La deuxième tangente issue de A est tangente au cercle en symétrique de R par rapport à (AI).

Le troisième côté est tangent au cercle et perpendiculaire à (AQ). Mener le rayon [IP] perpendiculaire à [IQ], la perpendiculaire en P à [IP] coupe (AQ) en C et (AR) en B.

Le triangle ABC est le triangle demandé.

Télécharger la figure GéoPlan tr_438_a.g2w

II.b. Hypoténuse et somme des côtés de l'angle droit

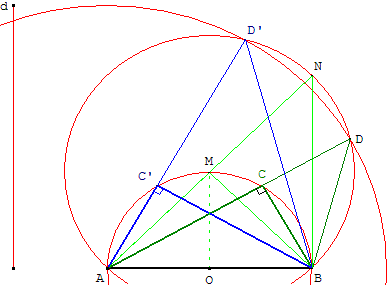
Tracer un triangle rectangle connaissant l'hypoténuse c et la somme d des côtés de l'angle droit

Supposons le problème résolu :

Soit ABC est le triangle rectangle en C demandé,
tel que AB = c et AC + CB = d.
Le point C est sur le cercle de diamètre AB.
Le cercle de centre A et de rayon d coupe la droite (AC) en D
tel que CD = CB.
Le triangle BCD est donc isocèle, mais comme l'angle en C est droit, il est aussi rectangle, l'angle ADB est égal à 45°.
D est donc sur l'arc capable qui « voit » le segment [AB] sous un angle de 45°.
Cet arc capable correspond à un angle au centre de 90°.

Le centre M de cet arc est à l'intersection du cercle de diamètre [AB] et de la médiatrice de [AB]. Sur le cercle de centre M passant par A et B, le point N est le symétrique de A par rapport à M.
Le triangle ANB est rectangle isocèle avec un angle ANB de 45°.

Le point D est donc à l'intersection du cercle de centre A et de rayon d et du cercle de centre M passant par A, et le point C est l'intersection de la demi-droite [AD) et du cercle de diamètre [AB].

Le problème admet une solution si les cercles sont sécants,
donc lorsque c < d ≤ 2AM.

Pour une hypoténuse [AB] donnée, si c < d  < 2AM on a quatre solutions : C et C’ et leurs symétriques par rapport à (AB) ; les quatre sommets d'un rectangle de centre O.

II.c. Médiane et hauteur relative à l'hypoténuse

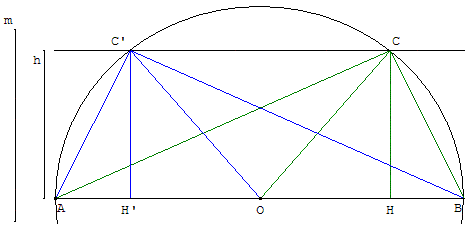
Tracer un triangle rectangle connaissant la médiane m et la hauteur h relative à l'hypoténuse

On sait que la médiane relative à l'hypoténuse [AB] est égale à la moitié de l'hypoténuse.
Placer le point O et de part et d'autre les points A et B tels que OA = OB = m.
Le point C est sur le cercle de diamètre [AB] à une distance h de (AB).

Le problème admet des solutions si h ≤ m.

Table des matières

Dans d'autres pages du site

Index triangles

La géométrie du triangle

La géométrie au collège

La géométrie en seconde

Copyright 2004 - © Patrice Debart

Téléchargement des anciennes versions de 2012

Télécharger tr_rectangle.pdf : ce document au format « .pdf » d'Adobe Acrobat

Copie sur d'autres sites

copie dégradée (sans accents ni images) :
https://www.etudier.com/dissertations/Triangle/62040196.html

studylibfr.com/doc/triangle-rectangle

La première page de ce document n'est pas une image,
mais Google trouve une erreur de type "soft 404".
Les copies ne devraient pas être référencées et
Google devrait choisir l'original au lieu du piratage !

Page n^o 70, réalisée le 23/6/2004
modifiée le 31/1/2016