Descartes et les Mathématiques

Géométrie du triangle I
Droites remarquables

Céviennes particulières d'un triangle : médianes, bissectrices, hauteurs, médiatrices.

I. Droites remarquables dans le triangle

II. Points caractéristiques du triangle

III Cercles remarquables

Cévienne

Dans un triangle, une cévienne est une droite issue d'un sommet :
    – les hauteurs, médianes, bissectrices sont des céviennes,
    – les médiatrices ne sont pas des céviennes.

Figure interactive dans GeoGebraTube : céviennes concourantes d'un triangle (point de concours à l'intérieur du triangle)

1. Rappel : barycentre de trois points

Ancienne classe de première S

Soit (A, α) ; (B, β) et (C, γ) trois points pondérés tels que α + β + γ ≠ 0, il existe un point unique G tel que :

α + β + γ =  ;

le point G est appelé barycentre des points pondérés (A, α) ; (B, β) et (C, γ).

Si α + β ≠ 0, α + γ ≠ 0 et β + γ ≠ 0 le théorème d'associativité permet de dire :

si A’ est le barycentre partiel de (B, β) et (C, γ), alors G est le barycentre de (A, α) et (A’, β + γ),
si B’ est le barycentre partiel de (A, α) et (C, γ), alors G est le barycentre de (B, β) et (B’, α + γ),
si C’ est le barycentre partiel de (A, α) et (B, β), alors G est le barycentre de (C, γ) et (C’, α + β) ;

les droites (AA’), (BB’) et (CC’) sont concourantes en G.

Coordonnées barycentriques

Soit A, B et C trois points du plan, tous distincts et non alignés.

Théorème de Gergonne (Joseph Gergonne 1771-1859) :
Pour tout point M du plan, il existe un triplet unique (α, β, γ) de nombres réels tels que :
    • α + β + γ = 1;
    • M est le barycentre des points pondérés (A, α) ; (B, β) et (C, γ).

(α, β, γ) sont les coordonnées barycentriques de M relativement à A, B et C.

Voir : le barycentre

2. Médianes et centre de gravité

Les médianes sont les droites joignant les sommets d'un triangle aux milieux des côtés opposés. Les trois médianes sont concourantes au centre de gravité du triangle, situé aux de chaque médiane à partir du sommet correspondant.

G centre de gravité, point X(2) de ETC.
en : centroid - intersection of the three medians

Voici cinq démonstrations du concours des médianes. Si on admet que les trois médianes sont concourantes il est possible de lire directement la première démonstration, sachant que, dans le triangle BCC₁, G est sur la droite des milieux (A’G) parallèle à (BC₁).

2.a. Symétrie centrale

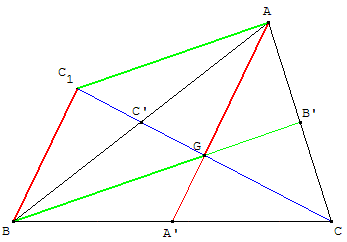
Soit G le point d'intersection des médianes [AA’] et [BB’] d'un triangle ABC.

Soit C₁ le symétrique de C par rapport à G.

Dans le triangle BC₁C, la droite des milieux (GA’) est parallèle à (BC₁), donc (GA) // (BC₁).
Dans le triangle AC₁C, la droite des milieux (GB’) est parallèle à (AC₁), donc (BG) // (AC₁).

AGBC₁ est un parallélogramme, car les côtés opposés sont, deux à deux, parallèles.

C’ est le milieu des diagonales et GC’ = GC₁ = CG.
CG = 2 GC’et CC’ = CG + GC’ = 3 GC’,
d'où GC’ = CC’ et CG = 2 GC’= CC’.
Le point G est situé aux de la médiane [CC’], à partir de C.

2.b. Somme des vecteurs + +

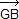Démontrer, avec un barycentre, que le centre de gravité se situe au deux tiers de la médiane d'un triangle, à partir du sommet.

Soit C₁ le quatrième sommet du parallélogramme AGBC₁.

+ = = 2 (règle du parallélogramme pour l'addition des deux vecteurs et C’ milieu de la diagonale)

G est le milieu de [CC₁] donc = −
et on a + + = .

Le centre de gravité G est l'isobarycentre des sommets d'un triangle ABC :

G est le barycentre des trois points pondérés (A, 1) ; (B, 1) et (C, 1) ;
donc + 2 = ;

G est le barycentre de (C, 1) et (C’, 2).

Le point G est situé aux , à partir de C, de la médiane [CC’].La fonction vectorielle de Leibniz permet d'écrire pour tout point M :
+ + = 3 .

2.c. Hexagone à côtés parallèles

Hexagone aux côtés opposés deux à deux parallèles

Soit G le point d'intersection des médianes [AA’] et [BB’] d'un triangle ABC.

Médiane (CC')
Placer le point C₁ image de A par la translation de vecteur .
On a = , d'où AGBC₁ est un parallélogramme de centre C’, milieu de [AB].

Comme côtés opposés du parallélogramme, on a (AC₁)//(BG),
d'où (AC₁)//(BB’).
(BB’) est donc une droite des milieux du triangle CAC₁ et coupe [CC₁] en son milieu.

De même (BC₁)//(AA’). (AA’) est une droite des milieux du triangle CBC₁ et coupe [CC₁] en son milieu.

Le milieu de [CC₁] est le point de concours des deux médianes (AA’) et (BB’) : c'est le point G.
Les points G, C’ et C₁ sont alignés sur la médiane issue de C.

Comme ci-contre, on montre que le point G est situé aux de la médiane [CC’].

Les trois médianes sont concourantes en G, centre de gravité du triangle

Médiane (AA')
Placer le point A₁ image de B par la translation de vecteur . = , d'où BGCA₁ est un parallélogramme de centre A’, milieu de [BC].
Les points G, A’ et A₁ sont alignés sur la médiane issue de A.

Médiane (BB')
Placer le point B₁ image de A par la translation de vecteur . = . AGCB₁ est un parallélogramme de centre B’, milieu de [AC].
Les points G, B’ et B₁ sont alignés sur la médiane issue de B.

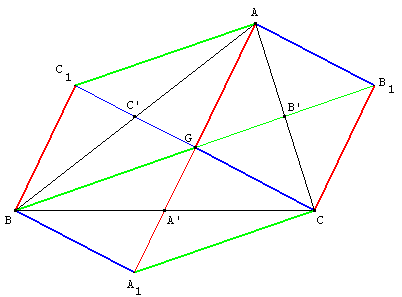
Trois autres parallélogrammes de centre G
Dans le parallélogramme AGBC₁, on a = , et dans BGCA₁, on a = ; d'où = . AC₁A₁C est un parallélogramme. G est le milieu des diagonales [AA₁] et [CC₁].

De même = = . BA₁B₁A est un parallélogramme.
Les diagonales [AA₁] et [BB₁] se coupent en leur milieu G.

Enfin les diagonales [BB₁] et [CC₁] se coupent en leur milieu G :
BC₁B₁C est un parallélogramme.

2.d. Parallélogramme de centre G

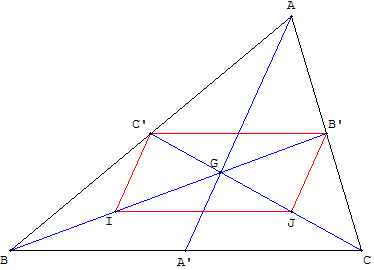
Classe de quatrième

Deux médianes sont concourantes au centre de gravité, point G situé aux de chacune d'entre elles.

Soit G le point d'intersection des médianes [BB’] et [CC’] d'un triangle ABC.
I est le milieu de [BG] et J est le milieu de [CG].

En appliquant le théorème des milieux dans les triangles ABC et GBC, on montre que C’B’ et IJ sont égaux à BC, et que (C’B’) et (IJ) sont parallèle à (BC).
IJB’C’ est donc un parallélogramme, car les côtés opposés [C’B’] et [IJ] sont de même longueur et parallèles.

Par hypothèse I milieu de [BG], on a BI = IG ;
G est le milieu des diagonales du parallélogramme, IG = GB’.

On en déduit que le point G est situé aux de la médiane [BB’] ; de même pour la médiane [CC’].

Ce même point G est situé aux de la troisième médiane

De même, en étudiant le parallélogramme IA’B’K où K est le milieu de [AG], on montre que les médianes [AA’] et [BB’] sont concourantes en un point situé à leurs . Ce point, situé aux de [BB’], est donc le point G. Les trois médianes sont concourantes en ce même point G, centre de gravité du triangle.

2.e. Tiers de la diagonale d'un parallélogramme

Classe de quatrième

Comment partager en trois de la diagonale d'un parallélogramme.

Par rapport au milieu O de [BC], tracer le symétrique D de A.

    – ABCD est un parallélogramme, de centre de symétrie O,
    – les points B’, C’ et I sont les milieux des côtés,
    – les points G et J sont les centres de gravité des triangles ABC et BCD.

Démonstration

    – Les points G et J partagent la diagonale [AD], du parallélogramme ABCD, en trois segments égaux :
AG = GJ = JD = AD.
Voir : figure d'Euclide dans partage en trois

Comme AD = 2 AO, on a AG = AD = AO.
On trouve encore que le centre de gravité G est aux de la médiane [AO].

Autre méthode

Méthode des aires : voir aires et triangles

2.f. Triangle médian

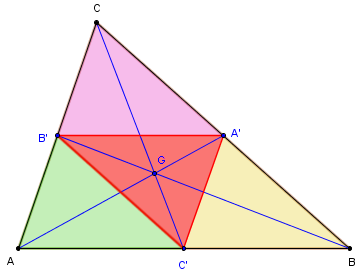
Le triangle A’B’C’, dont les sommets sont les pieds des médianes, est le triangle médian du triangle ABC.
On l'appelle aussi triangle complémentaire ou parfois triangle médial.

Comme G est au deux tiers des médianes et que GA = 2GA’, les points A, B et C sont les images de A’, B’ et C’ par l'homothétie h de centre G et de rapport –2.

Le triangle médian est l'homothétique du triangle ABC, par l'homothétie par réciproque h^{– 1}, de centre G et de rapport .

Les segments [A’B’], [B’C’] et [C’A’] partagent le triangle ABC en quatre triangles, d'aires égales au quart de celle du triangle initial.

Figure interactive dans GeoGebraTube : triangle médian

Le centre du cercle inscrit dans le triangle médian est le point de Spieker (X(10)). Il est sur la droite de Nagel (IG) qui joint le centre du cercle inscrit au centre de gravité.

Aire et médiane

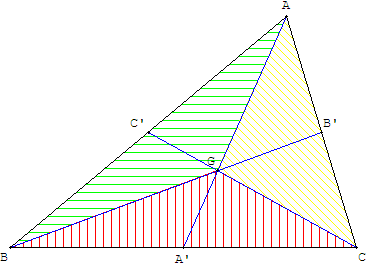
Une médiane partage un triangle en deux triangles d'aires égales.

Les droites des milieux partagent un triangle en quatre triangles homothétiques d'aires égales.

Partager un triangle en 6 triangles de même aire

Les trois médianes d'un triangle le partagent en six petits triangles d'aires égales.

Partager un triangle en 3 triangles même aire

Les trois triangles GAB, GBC et GAC sont d'aires égales.

Figure interactive dans GeoGebraTube : médianes d'un triangle

Partager un triangle en triangles d'aires égales

2.g. Théorèmes de la médiane

Premier théorème de la médiane − Théorème d'Apollonius

En géométrie analytique ou avec le produit scalaire, on peut vérifier les formes numériques des « théorèmes de la médiane » :

AB² + AC² = 2AA’² + (formule d'Apollonius de Perge − premier théorème de la médiane).

Voir démonstration avec la puissance d'un point par rapport à un cercle

Deuxième théorème de la médiane : calculs vectoriels des côtés et , avec la médiane :

Somme vectorielle de deux côtés du triangle : + = ( + ) + ( + ) = 2 , car + = .

On obtient alors la forme vectorielle du « théorème de la médiane » dans le triangle ABC :

+ = 2 .

Produit vectoriel de deux côtés du triangle : . = ( + ) . ( + ) = ² + . ( + ) + . ;
. = ² + ().() = ² – ².

On obtient la forme scalaire du « théorème de la médiane » dans le triangle ABC :

. = AA’² – BC².

Troisième théorème de la médiane

Avec le produit scalaire : AB² – AC² = ² – ² = ( + ).( – ) = 2 .(+ ) = 2 ..
Soit H, le point projeté orthogonal de A sur (BC). La projection de sur est , d'où . = . = ..

Donc AB² – AC² = 2 ..

D'où |AB² – AC²| = 2 BC × A’H  (troisième théorème de la médiane) ;

En effet, le produit scalaire de deux vecteurs colinéaires est égal à BC × A’H ou à son opposé, d'où la valeur absolue.

Application : lieux et théorèmes de la médiane

Longueur des médianes

Soit ABC un triangle tel que BC = a, AC = b, AB = c et m_A = AA’ la médiane relative au côté BC, d'après le « premier théorème de la médiane » on a :

b² + c² = 2m_A² + a²/2,

d'où m_A² = b²/2 + c²/2 - a²/4 donc m_A = .

2.h. Théorème des trois médianes

a. Si G désigne le centre de gravité du triangle ABC alors GA² + GB² + GC² = (a² + b² + c²).

    En effet GA = m_A d'où GA² = ()² m_A² = - a²/9 + 2b²/9 + 2c²/9 ; GB² = 2a²/9 - b²/9 + 2c²/9 et GC² = 2a²/9 + 2b²/9 - c²/9.
    La somme ds trois carrés donne GA² + GB² + GC² = (2/9) (a² + b² + c²) + (2/9) (a² + b² + c²) - (1/9) (a² + b² + c²) = [(2+2-1)/9] (a² + b² + c²) = (a² + b² + c²).

Théorème des trois médianes : la somme des carrés des médianes d'un triangle est égale aux trois quarts de la somme des carrés des côtés.

m_A² + m_B² +m_C² = (a² + b² + c²).

    En effet m_A = GA, m_B = GB et m_C = GC, d'où (m_A² + m_B² +m_C²) = ()²( GA² + GB² + GC²) = (a² + b² + c²).

b. Que devient cette propriété si on l'applique à un triangle équilatéral ? m = a,

c. Et si on l'applique à un triangle rectangle ? m_A² + m_B² +m_C² = (9/8) c²

Si A’ est les milieu d'un triangle ABC rectangle en C, AA’ est l’hypoténuse du triangle rectangle A’BC et m_A² = (a/2)² + b²,

De même m_B² = (b/2)² + a². On a m_C = c/2, donc m_A² + m_B² +m_C² = [(a/2)² + b² + (b/2)² + a² + (c/2)²] = [ a²/4 + b² + b²/4 + a² + c²/4] = [ c²/4 + c² + c²/4] = (9/8) c²

Pieds des médianes : D'un triangle ABC, il ne reste que les points I milieu de [AB], J milieu de [BC] et K milieu de [CA].
Reconstituer le triangle ABC, voir : le triangle, c'est le pied

3. Bissectrices du triangle et centre du cercle inscrit

3.a. Définitions

La bissectrice d'un angle est la droite qui, passant par le sommet de cet angle, le partage en deux angles de même mesure.

La bissectrice d'un angle est son axe de symétrie.

Théorème de la bissectrice : tout point de la bissectrice d'un angle est équidistant des côtés de cet angle.

Réciproque du théorème de la bissectrice : la bissectrice d'un angle est l'ensemble des points situés à égale distance des côtés de cet angle

Les bissectrices de deux angles supplémentaires adjacents sont perpendiculaires.

Télécharger la figure GéoPlan bissectr.g2w

I centre du cercle inscrit, point X(1) de ETC.

en : incenter - center of the incircle

« Comment construire le cercle tangent à un triangle »

Pour tracer le cercle inscrit dans un triangle, tangent aux trois côtés, construire deux bissectrices ; leur point d'intersection est le centre I du cercle. Projeter ce centre sur un des côtés : on trouve C₃, un des points de contact et il suffit alors de tracer le cercle de centre I, passant par ce point de contact C₃.

Tâche impossible

Trouver un triangle tel que deux bissectrices soient perpendiculaires !

3.b. Point de concours des bissectrices d'un triangle

Les trois bissectrices (intérieures) d'un triangle ABC sont concourantes en un même point I, centre du cercle inscrit dans le triangle (tangent intérieurement aux trois côtés du triangle).

Preuve

Soit I le point d'intersection de deux bissectrices issues de A et de B d'un triangle ABC.
I situé sur la bissectrice issue de A est à une distance r des côtés (AB) et (AC).
I situé sur la bissectrice issue de B, à une distance r du côté (BA), est situé à la même distance r de (BC).
I est donc équidistant de (AC) et de (BC). I est à l'intérieur du triangle, donc est situé sur la bissectrice intérieure issue de C.

Construction à la « règle et au compas », voir : problèmes de construction

Cercle inscrit dans le triangle

Le cercle inscrit est le plus grand cercle que peut contenir ce triangle.
Son centre I est le point de concours des bissectrices.

C'est le barycentre de (A, a) ; (B, b) ; (C, c)
avec a = BC, b = AC et c = AB.

Son rayon r est égal à =, où S désigne l'aire du triangle et p désigne le demi-périmètre : p =  (a + b + c).

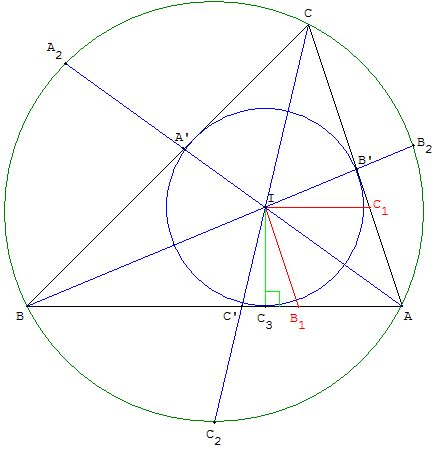
Les points d'intersection des bissectrices avec le cercle circonscrit sont les milieux des arcs déterminés par les sommets : A₂ est le milieu de l'arc BC, B₂ est le milieu de l'arc AC et C₂ est le milieu de l'arc AB.

Démonstration

Montrer que est la somme de deux vecteurs de même norme.

D'après la définition du barycentre I et en prenant le point A pour origine on a :

(a+b+c) = b + c .
Les vecteurs b et c ont la même norme bc.

Donc, = + = + .
Ces deux vecteurs ont même norme et AB₁IC₁ est un losange : la diagonale [AI] est la bissectrice de l'angle Â.

Voir : angles inscrits

3.c. Bissectrices extérieures et cercles exinscrits

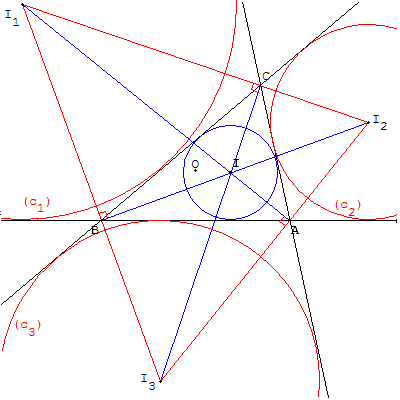
Les bissectrices extérieures partagent en deux l'angle bordé par un côté du triangle et le prolongement de l'autre côté.
En un sommet, les bissectrices intérieure et extérieure sont orthogonales.

Deux bissectrices extérieures, associées à deux sommets, et la bissectrice intérieure, associée au troisième sommet, sont concourantes.
Leur point d'intersection situé à égale distance des trois côtés du triangle est le centre d'un cercle exinscrit, tangent aux trois côtés du triangle.

Le point I₁, intersection de la bissectrice intérieure issue de A et des deux bissectrices extérieures issues de B et C,
est le barycentre de (A, – a) ; (B, b) ; (C, c).
I₁ est le centre du cercle (c₁) exinscrit au triangle,
son rayon est r₁ = = =
(en substituant S avec la formule de l'aire du triangle S =   bc sin A).

Relation d'Euler : OI₁² = R² + 2Rr₁.

Le point I₂, intersection de la bissectrice intérieure issue de B et des deux bissectrices extérieures issues de A et C,
est le barycentre de (A, a) ; (B, – b) ; (C, c).
I₂ est le centre du cercle (c₂) exinscrit au triangle, son rayon est  .

Le point I₃, intersection de la bissectrice intérieure issue de C et des deux bissectrices extérieures issues de A et B,
est le barycentre de (A, a) ; (B, b) ; (C, –c).
I₃ est le centre du cercle (c₃) exinscrit au triangle, son rayon est .

L'ensemble des points équidistants des droites (AB), (BC) et (AC) est formé des quatre points I, I₁, I₂ et I₃.

Le triangle I₁I₂I₃, formé par les bissectrices extérieures, de sommets les centres des trois cercles exinscrits, s'appelle le triangle de Bevan du triangle ABC.

Cercles tangents à trois droites : voir problème de contact DDD

Distances entre les sommets et les points de contact : voir cercles inscrit et exinscrit

Figure interactive dans GeoGebraTube : cercles inscrit et exinscrits

3.d. Bissectrices intérieure et extérieure

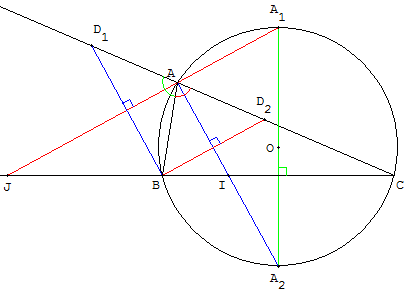
Les bissectrices recoupent le cercle circonscrit aux milieux des arcs déterminés par le côté opposé au sommet de l'angle.

Dans l'exemple ci-contre pour le sommet A du triangle ABC direct,
la bissectrice intérieure (AI) recoupe le cercle circonscrit en A₂ qui est le milieu de l'arc BC (parcouru dans le sens trigonométrique) ;
la bissectrice extérieure (AJ) recoupe le cercle circonscrit en A₁ qui est le milieu de l'autre arc BC, lorsque l'on parcourt le cercle en sens inverse.

Dessin des bissectrices à partir du cercle circonscrit

Soit ABC un triangle inscrit dans un cercle (c).
Tracer le diamètre [A₁A₂] porté par la médiatrice de [BC].
(AA₂) et (AA₁) sont les bissectrices des angles, de sommet A, formés par les droites (AB) et (AC).

Confusion : dans la page comment-retrouver le centre d'un cercle en 5 ^eme, confusion de cette figure avec celle des médiatrices

Théorème (du pied) de la bissectrice : IB/IC = c/b

Une bissectrice intérieure de l'angle d'un triangle partage le côté opposé en deux segments de longueurs proportionnelles à celles des côtés adjacents.

La bissectrice intérieure d'un triangle divise le côté opposé en deux segments proportionnels aux deux autres côtés.

Démonstration d'une division harmonique par Thalès

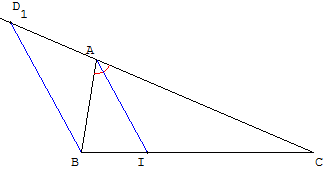
Le pied de la bissectrice sur [BC] est I.
On pose AB = c et AC = b.
La parallèle à (AI) passant par B coupe (AC) en D₁.
Le calcul des angles permet de montrer que le triangle ABD₁ est isocèle.
Donc, AD₁ = AB = c.

La propriété de Thalès, dans le triangle BCD₁, montre que IB/IC = AD₁/AC = c/b.
I est le barycentre de (B, b) et (C, c).

De même (figure de gauche ci-dessus), le pied de la bissectrice extérieure sur (BC) est J ; la parallèle à (AJ) passant par B coupe (AC) en D₂.
Le triangle ABD₂ est isocèle et AD₂ = AB = c.
La propriété de Thalès dans le triangle JAC montre que JB/JC = AD₂/AC = c/b.
J, à l'extérieur de [BC], est le barycentre de (B, – b) et (C, c).

IB/IC = JB/JC = c/b : les quatre points [B, C, I, J] forment une division harmonique de rapport c/b.

Relations métriques

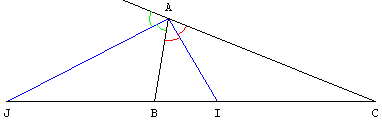
AB × AC = AI² + IB × IC.

AB × AC = JB × JC – AJ².

3.e. Axe anti-orthique

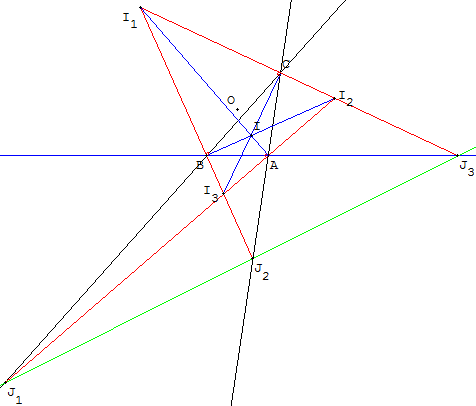
Droite qui passe par les pieds des bissectrices extérieures d'un triangle.

Télécharger la figure GéoPlan axe_anti_ortique.g2w

4. Hauteurs et orthocentre

Classe de cinquième

Les hauteurs sont les perpendiculaires abaissées d'un sommet sur le côté opposé.
Les trois hauteurs sont concourantes au même point H orthocentre du triangle.

L'orthocentre, est le point X(4) de ETC

en : orthocenter - intersection of three altitudes

Figure interactive dans GeoGebraTube : hauteurs du triangle

Remarques :

• Un triangle est rectangle si et seulement si son orthocentre est un des sommets du triangle
• Un triangle est acutangle (dont les trois angles sont aigus) si et seulement si son orthocentre est à l'intérieur du triangle
• Un triangle est obtusangle (ayant un angle obtus) si et seulement si son orthocentre est à l'extérieur du triangle.

Montrer que les hauteurs d'un triangle sont concourantes

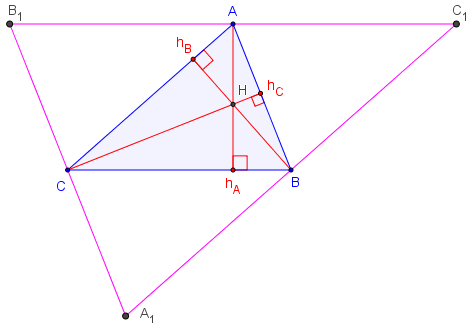
Classe de quatrième

Soit (Ah_A), (Bh_B) et (Ch_C) les hauteurs d'un triangle ABC.

Les parallèles aux côtés du triangle ABC, passant par les sommets opposés, forment un triangle A₁B₁C₁ où A, B et C sont les milieux des côtés.

Les hauteurs (Ah_A), (Bh_B) et (Ch_C) perpendiculaires aux milieux des côtés du triangle A₁B₁C₁ sont les médiatrices de ce triangle. Elles sont concourantes au point H, centre du cercle circonscrit à A₁B₁C₁.

Les hauteurs du triangle médian ABC sont donc concourantes en H.

Figure interactive dans GeoGebraTube : les hauteurs d'un triangle sont concourantes

Barycentre et hauteurs d'un triangle

Classe de premiière

L'orthocentre H est le barycentre de [A, tan(Â)] ; [B, tan(B)] ; [C, tan(C)].

4.a. Quadrangle

Quadrilatère orthocentrique (ou groupe orthocentrique)

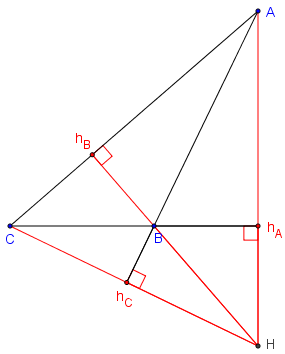
Définition : chaque sommet du quadrangle est l'orthocentre du triangle ayant pour sommets les trois autres points.

Si H est l'orthocentre du triangle ABC,
A est l'orthocentre de BCH, B l'orthocentre de ACH, C l'orthocentre de ABH.

ABCH est un quadrangle orthocentrique.

4.b.Symétriques de l'orthocentre

en : symmetrical of the orthocentre

Notations
H est l'orthocentre du triangle ABC ;
A’ : B’ : C’ ; les milieux des cotés ;
h_A, h_B, h_C les pieds des hauteurs.

Symétriques de l'orthocentre

Les intersections f_A, f_B, f_C des hauteurs avec le cercle circonscrit sont les symétriques de H par rapport aux côtés du triangle.

Les symétriques s_A, s_B, s_C de l'orthocentre par rapport aux milieux des côtés se trouvent sur le cercle circonscrit.

Figure interactive dans GeoGebraTube : symétriques de l'orthocentre

Démonstration - voir droite d'Euler

grec : Γεωμετρια − Exemple de figure géométrique

4.c. Construction au compas seul

Ci-dessous deux constructions au compas avec des cercles définis par symétrie ou définis par des points cocycliques.

Nous exploiterons ces figures pour démontrer les propriétés du triangle orthique ou le théorème de Clifford.

Quatre cercles de même rayon

Tracer le centre O du cercle circonscrit (c) au triangle ABC.
Construire le point O₁ symétrique de O par rapport à (BC).
Le cercle (c₁) de centre O₁ passant par B et C est symétrique du cercle circonscrit.
De même tracer les centre symétriques O₂ et O₃ et les cercles (c₂) et (c₃).
Ces trois cercles se coupent en H, orthocentre du triangle, ce qui permet de construire les trois hauteurs (AH), (BH) et (CH) avec un compas.

Cercles circonscrits

Les symétries par rapport aux côtés du triangle transforment le cercle circonscrit au triangle ABC en des cercles passants par H : les cercles circonscrits au triangle ABC et aux triangles AHB, BHC et CHA sont de même rayon.

Démonstration

Les symétriques f_A , f_B et f_C de l'orthocentre par rapport aux côtés du triangle sont situés sur le cercle circonscrit au triangle.

L'orthocentre H symétrique de f_A est situé sur le cercle (c₁) symétrique du cercle circonscrit (c),
de même H est sur les cercles (c₂) et (c₃).

Voir : droite d'Euler

Figure interactive dans GeoGebraTube : quatre cercles de même rayon

Les quatre points A, B, C et H jouissent de la propriété que l'un d'entre eux est l'orthocentre du triangle formé par les trois autres.
A est l'orthocentre de BCH, B l'orthocentre de ACH, C l'orthocentre de ABH.
On dit que les quatre points forment un groupe orthocentrique.

Voir aussi : groupe orthocentrique dans l'espace

4.d. Tracer les hauteurs d'un triangle avec un compas

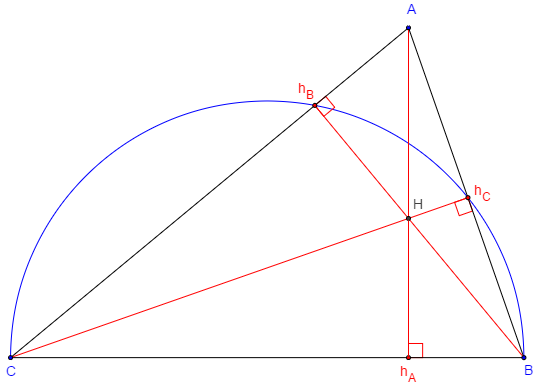
Les trois hauteurs d'un triangle sont concourantes au même point H.

ABC est un triangle ayant un angle aigu en A.

h_B et h_C les pieds des hauteurs.

Les hauteurs (Bh_B) et (Ch_C) se coupent en H.

La droite (AH) coupe [BC] en h_A.

Les angles droits Bh_BC et Bh_CC sont inscriptibles dans une même demi-circonférence de diamètre [BC].

Démonstration d'Archimède (287-212 avant J.-C.)

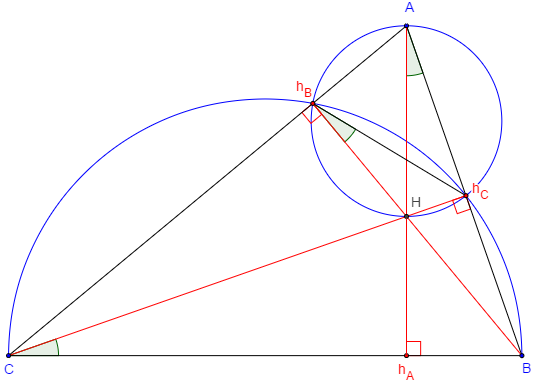
Pareillement les quatre points h_B, A, h_C et H sont sur une même circonférence de diamètre [AH].
Dans ce cercle, les angles inscrits Hh_Bh_C et HÂh_C sont égaux.

Dans le demi-cercle les angles inscrits BCh_C et Bh_Bh_C sont aussi égaux ;
par suite BAh_A = BCh_C car égaux à l'angle Bh_Bh_C ;
les triangles ABh_A et BCh_C, ayant en outre l'angle B en commun, sont semblables.
Le triangle ABh_A est aussi rectangle : l'angle Ah_AB est droit et (AH) est la troisième hauteur qui coupe [BC] en h_A.

Figure interactive dans GeoGebraTube : hauteurs - démonstration d'Archimède

Si ABC est acutangle (dont les trois angles sont aigus) H est le centre du cercle inscrit dans h_Ah_Bh_C
et les points A, B, C sont les centres des cercles exinscrits à h_Ah_Bh_C.

WikiPédia : Hauteurs d'un triangle

Construire un triangle connaissant ses trois hauteurs

5. Médiatrices du triangle et centre du cercle circonscrit

Triangle inscrit dans un cercle

O centre du cercle circonscrit, point X(3) de ETC.

en : circumcenter - center of the circumscriebed circle

Figure interactive dans GeoGebraTube : médiatrices d'un triangle

      Feuille de travail dynamique avec GeoGebra – Figures classiques

Retrouver cette figure : problème de contact PPP

Application : retrouver le centre d'un cercle

Retrouver le centre avec la règle à bords parallèles

Problème de Napoléon : construction au compas seul

Construire un triangle connaissant ses médiatrices

WikiPédia : Médiatrice

Accompagnement du programme de 5^e

Dans le cas du concours des médiatrices d'un triangle, c'est la caractérisation de la médiatrice d'un segment à l'aide de l'équidistance qui intervient. Elle est mobilisée deux fois dans un sens et une fois dans l'autre sens.

La médiatrice d'un segment est la droite perpendiculaire au segment en son milieu. C'est l'ensemble des points équidistants des extrémités du segment.
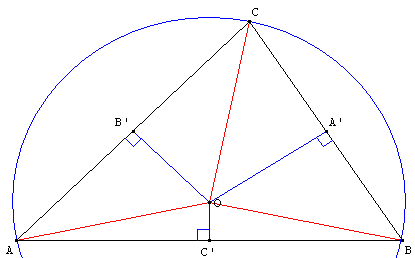
Les trois médiatrices d'un triangle sont concourantes au même point, centre du cercle circonscrit au triangle.

A’, B’ et C’ sont les milieux des côtés du triangle ABC.

Soit O l'intersection des médiatrices de [AB] et de [BC].
Pour la médiatrice (OC’) on a OA = OB et pour (OA’) on a OB = OC.
D'où par transitivité OA = OC ; O appartient à la médiatrice de [AC].
Les trois médiatrices sont concourantes en O, centre du cercle circonscrit.

Remarques :

• Un triangle est acutangle si et seulement si les médiatrices se coupent à l'intérieur du triangle
• Un triangle est obtusangle si et seulement si les médiatrices se coupent à l'extérieur du triangle

Barycentre

Le point O est le barycentre de [A, sin(2A)] ; [B, sin(2B)] ; [C, sin(2C)].
Avec la relation vectorielle d'Euler = + + ,
on trouve aussi que O est le barycentre des trois points pondérés :
[A, tan(B) + tan(C)] ; [B, tan(Â) + tan(C)] ; [C, tan(Â) + tan(B)].

Droites remarquables du triangle isocèle

La médiatrice de la base d'un triangle isocèle est axe de symétrie du triangle.
Les autres droites remarquables (médiane, hauteur, bissectrice) relatives à la base sont confondues avec cette droite.