Descartes et les Mathématiques
Partage d'un segment en trois
Le tiers d'un segment avec des parallélogrammes, ou avec les configurations du triangle.
Sommaire
1. Tracé de médianes
2. Configuration de Thalès
3. Tracé de parallèles dans un rectangle
4. Parallélogramme et milieux : partage en trois d'une diagonale
5. Partage en trois du côté d'un parallélogramme
6. Figures incomplètes et configuration : tiers d'un segment
Voir aussi règle à bords parallèles
Pliage d'une feuille en trois parties égales : constructions par pliages
Partage en trois d'une diagonale du cube
Partages du cercle en trois parties égales
Pour partager un segment en trois parties égales
• Configuration de Thalès : Couper le segment en trois avec des parallèle équidistantes
• Configuration du triangle : Tracé de médianes en s'appuyant sur la propriété du centre de gravité.
• Géométrie dynamique
Avec GéoPlan le partage d'un segment [AB] en trois peut se faire directement avec un repère (A,B) sur la droite, en plaçant les points I et J d'abscisses 
et 
, sans passer par une construction à la règle et au compas.
Avec GeoGebra, utiliser les barycentres : I est le barycentre de (A, 2) et (B,1) ; saisir I = (2A + B)/3
J est le barycentre de (A, 1) et (B,2) ; saisir J = (A + 2B)/3
Partager un segment en trois parties égales
1. Tracé de médianes
Classe de première L
Partage en trois s'appuyant sur la propriété du centre de gravité.
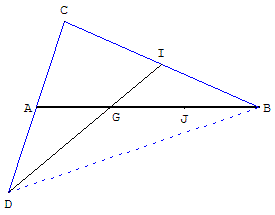
Placer un point I à l'extérieur de (AB).
Symétrique C de B par rapport à I : sur la droite (BI) reporter la longueur BI et placer le point C tel que IC = BI.
Symétrique D de C par rapport à A : sur la droite (CA) reporter la longueur CA et placer le point D tel que AD = CA.
La droite (DI) coupe (AB) en G. Le point G est au tiers de [AB].
En effet, G, point d'intersection des médianes, est le centre de gravité du triangle BCD.
En reportant la longueur AG sur (AB), on trouve le point J milieu de [GB], situé au de [AB] à partir de A.
Télécharger la figure GéoPlan tier_seg.g2w
2. Configuration de Thalès
Classes de quatrième et troisième
Couper un segment en trois avec Thalès
Cet exercice repose sur la propriété de Thalès, mais peut être utilisé avant de l'avoir justifiée.
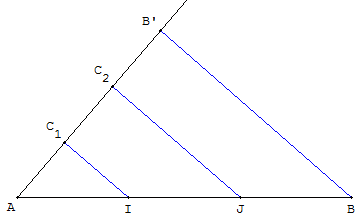
Tracer sur demi-droite issue de A, 3 segments égaux [AC1], [C1C2], [C2B’].
Ce tracé se fait facilement, à la règle et au compas : placer un point C1 à l'extérieur de (AB), et sur la demi-droite [AC1), tracer le symétrique C2 de A par rapport à C1, puis le symétrique B’ de C1 par rapport à C2.
Tracer le segment [BB’] et les parallèles à (BB’) passant par C1 et C2.
En I et J, elles découpent [AB] en 3 parties égales.
Télécharger la figure GéoPlan diviser_segment_en_3.g2w.g2w
Voir aussi : Diviser un segment en 4 parties égales,
Diviser un segment en 5 parties égales…
Diviser un segment en n parties égales
3. Tracé de parallèles dans un rectangle
Partager un segment en 3 en dessinant des parallèles dans un rectangle
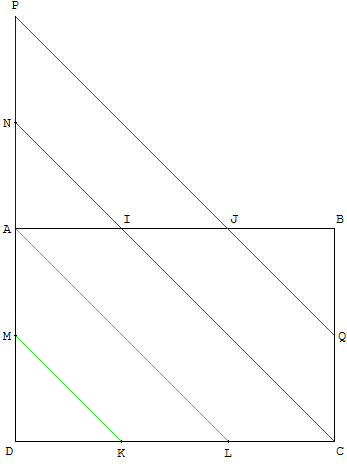
Sur la perpendiculaire en A à (AB) placer un point D, puis terminer le rectangle ABCD.
Tracer les milieux M de [AD] et Q de [BC], puis les symétriques N et P de M et D par rapport à A.
En I et J, les droites parallèles (NC) et (PQ) coupent [AB] en trois parties égales.
Il est possible de justifier cette construction par la propriété de Thalès : [AB] est partagé en trois parts égales par un faisceau de parallèles équidistantes.
De plus deux autres parallèles à (NC) partagent [DC] en trois parties égales en K et L.
Télécharger la figure GéoPlan cons_rect_perpendiculaires.g2w
Autre figure, voir Cabri en sixième
4. Parallélogramme et milieux : partage en trois d'une diagonale
Les Éléments d'Euclide, livre III
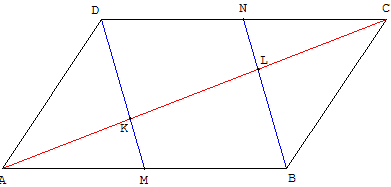
Dans un parallélogramme, les segments, joignant deux sommets opposés aux milieux des côtés opposés, sont parallèles et partagent la diagonale joignant les deux autres sommets en trois parties égales.
Solution 1
Classe de quatrième
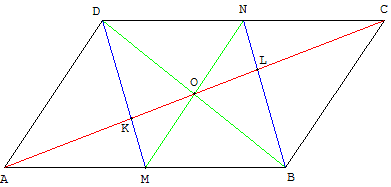
ABCD est un parallélogramme de milieu O, M est le milieu de [AB] et N est le milieu de [CD].
O est le milieu commun de la diagonale [BD] et de la médiane [MN].
MBND est un parallélogramme et (MD) est parallèle à (BN).
M est le milieu de [AB] donc, dans le triangle ABL, le point K est le milieu de [AL] et AK = KL,
N est le milieu de [CD] donc, dans le triangle CDK, le point L est le milieu de [KC] et KL = LC.
K et L partagent [AC] en trois segments de longueur égale.
Commande GéoPlan, figure parallelogramme_milieu.g2w :
Solution 2
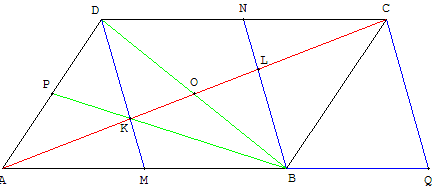
Soit M le milieu de [AB], N le milieu de [AB] et P le milieu de [AD].
Le point O, intersection des diagonales [AC] et [BD], est le milieu de ces diagonales.
Les droites (AO), (BP) et (DM), médianes du triangle ABD, sont concourantes en K, centre de gravité de ce triangle.
Soit Q le symétrique de M par rapport à B.
On a AM = MB = BQ et (DM) // (NB) // (CQ), car MBND et BQCN sont des parallélogrammes.
Le théorème de Thalès par rapport à ces trois parallèles et aux deux sécantes (AQ) et (AC) permet de conclure :
AK = KL = LC.
5.a. Partage en trois du côté d'un parallélogramme
Construire le 1/3 d'un segment
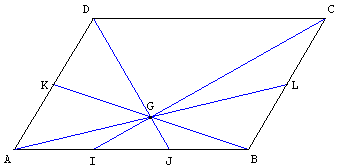
On considère un segment [AB] et on trace un parallélogramme ABCD.
Soit K est le milieu de [AD], L le milieu de [BC].
Les diagonales du parallélogramme ABLK se coupent en G.
Les droites (CG) et (DG) déterminent sur le côté [AB] deux points I et J qui le partagent en trois parties égales.
Télécharger la figure GéoPlan bary_f19.g2w
Voir alignement et concours : barycentre
Cas particulier du rectangle - pliage d'une feuille en trois parties égales : constructions - pliages
Applications
5.b. Réciproque : centre de gravité d'un triangle
Le centre de gravité d'un triangle est situé aux des médianes à partir des sommets :
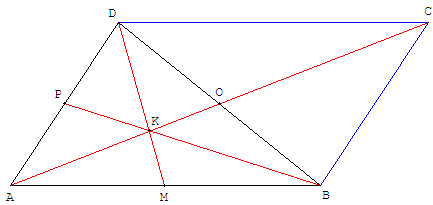
À partir d'un triangle ABD, construire le point C, symétrique de A par rapport au milieu O de [BD], permet d'obtenir le parallélogramme de la figure ci-dessus. [AO] et [CM] sont deux médianes de ABD qui se coupent en K, centre de gravité du triangle.
AK = AC = AO car AO = 
AC.
Le point K situé au tiers de la diagonale [AD] est aux deux tiers de la médiane [AO].
Télécharger la figure GéoPlan centre_gravite_ds_parallelogramme.g2w
Voir : médianes dans géométrie du triangle
5.c.et 5.d. Deux cas particuliers :
5.c. Perpendiculaires dans un parallélogramme ou dans un rectangle
Droites perpendiculaires dans un parallélogramme particulier
Si le parallélogramme ABCD est tel que AB = 2 AD = 2a, MBCN est alors un losange de côté a, les diagonales (BN) et(MC) sont perpendiculaires.
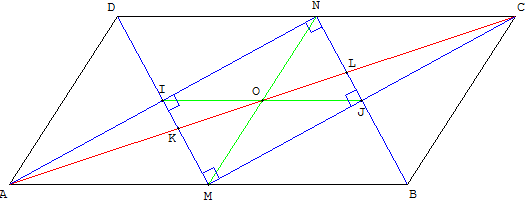
Soit I et J les milieux des losanges AMND et MBCN.
Dans le triangle ABN, la droite des milieux (IJ) est parallèle à (AB) et IJ = a.
Cette droite (IJ) est une droite des milieux des triangles AMN et MBN. Elle passe par le milieu O de [MN]. Comme IO = a/2 et OJ = a/2, O est le milieu de [IJ]. Les diagonales [IJ] et [MN] de IMJN sont de même longueur a et se coupent en leur milieu O, donc IMJN est un rectangle.
[IJ], [MN] et [AC] ont même milieu O.
Télécharger la figure GéoPlan parallelogramme_milieu_rect.g2w
5.d. …dans un rectangle particulier
Classe de 2nde
Dans un rectangle ABCD, les droites (MD) et (BN) sont perpendiculaires à la diagonale (AC),
si AB = 
CD.
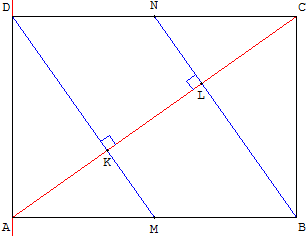
Indications
Soit AD = a, AB = b.
Dans le triangle rectangle ABC : AC2 = a2 + b2,
Comme AK = AC/3 on a AK2 = (a2 + b2)/9.
K est le centre de gravité du triangle ABD situé aux de la médiane [DM].
Dans le triangle rectangle AMD, DM2 = a2 + b2/4 ;
la hauteur AK, issue de l'angle droit est la moyenne géométrique entre les projections des petits côtés sur l'hypoténuse :
AK2 = DK × KM = DM × DM/3 = (2/9)DM2.
Soit AK2 = (2a2 + b2/2)/9.
En identifiant 9AK2 : a2 + b2 = 2a2 + b2/2, soit a2 = b2/2, relation annoncée.
Télécharger la figure GéoPlan rectangle_milieu.g2w
6. Figures incomplètes : tiers d'un segment
6.a. Trouver un alignement
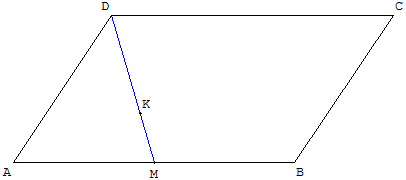
ABCD est un parallélogramme, M est le milieu de [AB] et K est situé au tiers de [MD].
Que penser du point K ? Quel segment tracer pour trouver une solution ?
Solution
K est situé sur la diagonale [AC].
Indications
Point de vue des configurations : tracer les diagonales [AC] et [BD] qui se coupent en O.
K est le centre de gravité du triangle ABD, situé aux deux tiers de la médiane [AO], donc au tiers de [AC].
Géométrie analytique : tracer la diagonale [AC].
Dans le repère (A, 
, 
), à partir des coordonnées des points M(, 0) ; C(1, 1) et D(0, 1),
on calcule celles des vecteurs 
(, 0) ; 
(-, 1) ;
d'où 
= , 
(-
, )
et comme 
= + ,
on a (, ).
On a donc = 
; A, K et C sont alignés.
Télécharger la figure GéoPlan parallelogramme_incomplet.g2w
6.b. Montrer un alignement
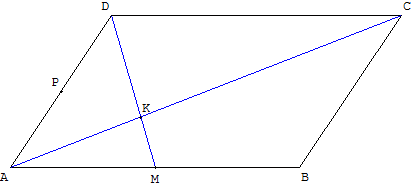
Soit ABCD un parallélogramme, M et P les milieux respectifs de [AB] et [AD] et K le point d'intersection de(AC) et (DM).
Démontrer que les points B, K et P sont alignés.
Configuration : médianes et centre de gravité
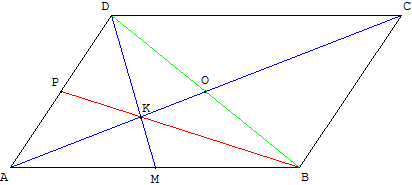
Tracer la diagonale [BD], qui coupe la diagonale [AC] en son milieu O.
[AO] et [DM] sont les médianes du triangle ABD, leur point d'intersection K est le centre de gravité.
La troisième médiane [BP] passe par le centre de gravité K.
Les points B, K et P sont bien alignés.
Télécharger la figure GéoPlan parallelogramme_alignement.g2w
Voir aussi point aligné sur une diagonale : parallélogramme de Pappus
7. Parallélogramme et homothétie
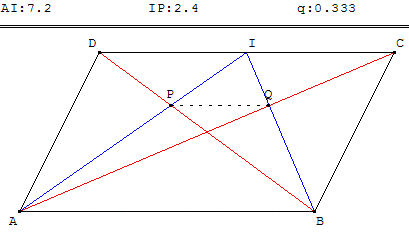
ABCD est un parallélogramme et I le milieu [CD].
Les diagonales du parallélogramme coupent [IA] en P et [IB] en Q.
Que représente le point P dans le triangle ACD et le point Q dans le triangle BCD ?
En utilisant une homothétie de centre I,
montrer que (PQ) // (AB) et que PQ = 
.
Télécharger la figure GéoPlan hom_par5.g2w
8. Règle à bords parallèles
Avec la règle à bords parallèles seule, on peut construire le milieu d'un segment, on peut aussi le partager en trois :
Construction du tiers avec un parallélogramme
Pour trouver le tiers d'un segment, on peut construire un parallélogramme ayant pour côté ce segment.
En traçant le tiers de la diagonale et en projetant parallèlement à l'autre côté on obtient le point T au tiers de [AB].
Dans le plan projectif, en appelant E le point de concours à l'infini des droites (AD) et (BC), on obtient la figure ci-contre à droite, où T au tiers de [AB].
La justification ci-dessous en découle.
Télécharger la figure GéoPlan tiers_ds_parallelogramme.g2w
Construction du tiers avec la règle à bords parallèles
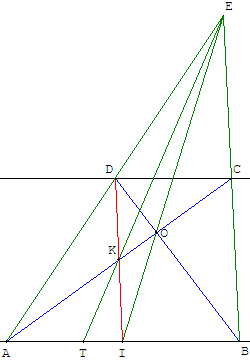
Avec la règle à bords parallèles, tracer une parallèle à (AB) et y choisir un point D.
Sur la demi-droite [AD), à l'extérieur de [AD], placer un point E.
Avec C sur (BE), on trace le quadrilatère ABCD, ayant deux côtés parallèles.
Les diagonales se coupent en O et, par la construction d'Hilbert, I est le milieu de [AB].
Le point K est l'intersection de (AC) et (DI).
Le point T, intersection de (AB) et (EK), est au tiers de [AB].
Télécharger la figure GéoPlan tiers_ds_parallelogramme.g2w
Utilisation de l'espace pour un problème plan
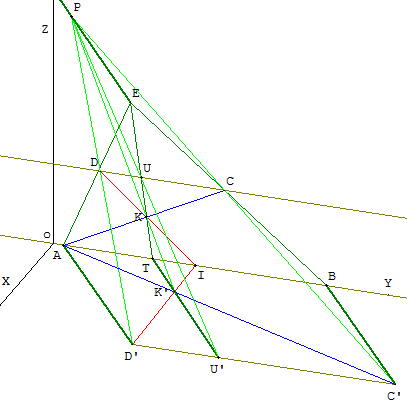
Démonstration « par le relief » avec une perspective
Choisir deux points A, B et leur milieu I sur la demi-droite [oY).
Tracer le quadrilatère ABCD, ci-dessus à droite, dans le plan vertical (oYZ).
Dans le plan horizontal (oXY), choisir un point D’ et construire le parallélogramme ABC’D’.
Les droites (DD’) et (CC’) se coupe en P situé la parallèle à (AD’) passant par E.
La perspective de centre P transforme ABCD en ABC’D’.
Le point K a pour image le point K’ situé au tiers de la diagonale [AC’].
La droite (EK) a pour image (K’U’) parallèle à (AD’). Ces deux droites se coupent en T qui est bien le tiers de [AB].
Télécharger la figure GéoSpace tiers_perspective.g3w
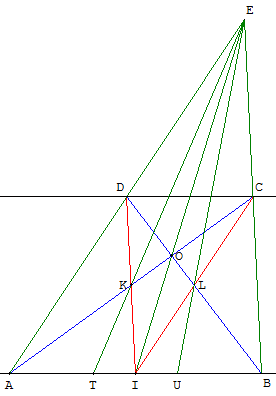
Prolongement : avec l'intersection de (BD) et (CI), on peut trouver un point L
Le point U, intersection de (AB) et (EL), est au deuxième tiers de [AB].
9. Réseau de losanges avec des triangles équilatéraux
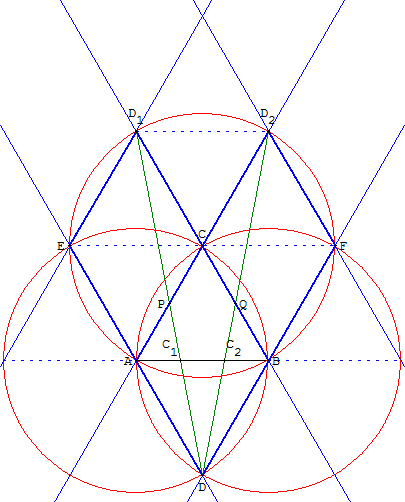
À l'aide d'un instrument, construire trois losanges dans un réseau de triangles équilatéraux, ayant des côtés de longueur AB.
Ci-contre une construction avec trois cercles de même rayon :
tracer les cercles de centre A passant par B et de centre B passant par A,
construire C, un des points d'intersection des deux cercles,
terminer en traçant le cercle de centre C passant par A.
En traçant les segments [DD1] et [DD2] reliant les sommets de ces losanges, on trouve les milieux P et Q des côtés du losange ACBD, et on en déduit les points C1 et C2 partageant le segment [AB] en trois parties égales.
On retrouve le partage en trois de la diagonale du parallélogramme ACBD, par les droites (DP) et (DQ) joignant D aux milieux des côtés opposés.
Voir le cas plus général de cette méthode avec la construction de losanges grâce à la règle à bords parallèles
Télécharger la figure GéoPlan regle_diviser_4.g2w
Table des matières
Dans d'autres pages du site
Division d'un segment en parties égales
Les problèmes de partage en parts égales
Mathématiques.net : Couper un segment en trois
Faire de la géométrie en seconde
Google friendly
Page no 170, réalisée le 6/4/2011