Descartes et les Mathématiques

Constructions par pliage

Origamis réalisés avec un logiciel de géométrie dynamique.

Sommaire

1. Pliage d'une feuille

2. Partage d'une feuille en 3 parties égales

3. Partage en cinq de la diagonale d'un rectangle

4. Pliage d'un rectangle selon une diagonale

5. Pliage d'un triangle selon une droite des milieux

6. Triangle équilatéral
      par pliage d'un cercle
      par pliage d'une bande rectangulaire

      par pliage d'une feuille carrée

7. Pentagone régulier

8. Hexagone régulier

1. Pliage d'une feuille (ou origami)

Cet art, originaire de la Chine, regroupe les techniques de pliage de papier. Le mot origami vient du japonais.

L'origami est une technique plus puissante que « la règle et le compas » et le formalisme du pliage d'une feuille de papier permet de réaliser (sans autre instrument) :

• le tracé d'une droite,
• la perpendiculaire à une droite,
• la médiatrice d'un segment,
• le milieu d'un segment,
• les bissectrices d'un angle,
• un angle de 60° ou de 30°,
• la trisection de l'angle.

Tracé d'une droite

Plier selon deux points A et B. c'est le tracé de la droite (AB)

Perpendiculaire à une droite

Plier une feuille le long de la droite, puis plier une seconde fois en superposant les deux bords du pli précédent. On a fabriqué un angle droit.
Si on déplie la feuille, les deux plis forment deux droites perpendiculaires.

Médiatrice et milieu d'un segment

Par pliage d'une feuille rabattre un point A sur un point B : appuyer le pli de la feuille qui marque la médiatrice de [AB].
En réalisant un second pli passant par A et B, on obtient deux plis qui permettent la construction du milieu de [AB].

Bissectrice de deux droites

Deux droites (d) et (d’) étant inscrites sur une feuille, amener (d) en coïncidence avec (d’), la trace du pli donne un axe de symétrie : une bissectrice lorsque les deux droites ne sont pas parallèles.
Si les deux droites sont concourantes en un point I situé sur la feuille, il y a deux façons de faire le pli permettant d'obtenir les deux bissectrices.
Si le point de concours de deux droites est situé hors de la feuille, c'est une construction d'une bissectrice passant par une intersection inaccessible.

Triangle équilatéral

Triangle équilatéral par pliage d'une feuille rectangulaire,

triangle équilatéral à partir d'un cercle.

Pentagone

Construction d'un pentagone régulier : en réalisant un nœud avec une bande ;

    en pliant une feuille.

Hexagone

Parallèle à une droite passant par un point donné

Une droite (d) et un point A étant donnés, plier la feuille le long de la droite par un pli passant par A. On obtient la perpendiculaire (d’) à (d) en A.
Un second pli en A le long de (d’) permet de tracer la perpendiculaire à (d’) en A, qui est la parallèle à (d) cherchée.

Intersection d'une droite et d'un cercle

Une droite (d) et deux points A et B étant donnés, il est possible de trouver une des intersections du cercle de centre B, passant par A, en amenant le point A sur la droite (d) avec un pli passant par B.

Droite passant par un point et l'intersection inaccessible de deux droites

Trisection de l'angle

Enveloppes de coniques : parabole,   ellipse et hyperbole

Sciences amusantes

On ne peut pas plier, sur elle-même, une feuille de papier (A4 - 80 grammes) plus de 7 à 8 fois.
Au 7^e pliage, on plie 128 feuilles, au 8^e pliage, on plie 256 feuilles, l'arc de cercle formé par le pli devient alors trop grand.

Mais avec une très grande longueur de papier toilette, on peut réaliser jusqu'à 12 pliages.

2. Partage d'une feuille en trois parties égales

Diviser un segment en 2, 4, 8… parties égales par pliage est facile.

Pour d'autres divisions, rechercher des solutions souvent basées sur Thalès.

2.a. Deux diagonales

Tracer une diagonale d'une feuille rectangulaire puis, sans extrémité commune, une diagonale du demi-rectangle. Elles se rencontrent en I, au tiers de la hauteur et au tiers de la largeur de la feuille.

Justification : voir partages en trois

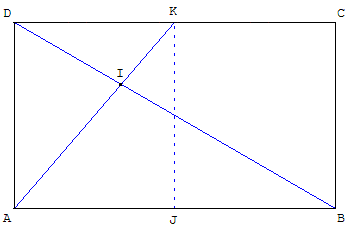
Cas particulier : si ABCD est une feuille au format A4 (AB = CD).
Les droites (AK) et (BD) sont perpendiculaires.

Indications : appliquer la réciproque du théorème de Pythagore dans le triangle AIB, sachant que I est aux deux tiers de chaque diagonale.

Pour le partage en 3 (ratio = 0,33), utiliser la figure de GeoGebraTube partage de la diagonale d'un rectangle avec e = DK = 1/2.
Valider e = 0.5 dans la ligne de saisie.

2.b. Réseau de droites parallèles

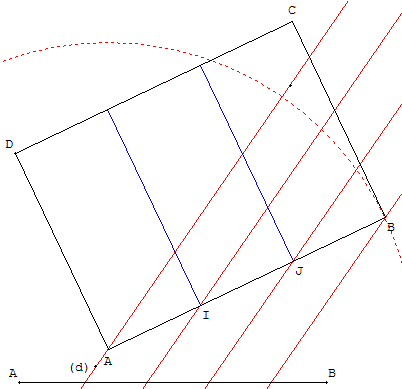
À partir d'un réseau de quatre droites parallèles, on sait poser dessus la feuille de papier et l'incliner de telle façon que deux coins d'un bord soient situés sur les deux parallèles extrêmes.
Les deux autres parallèles intérieures déterminent sur le bord deux points qui permettront le partage de la feuille en trois.

Voir partage d'un segment en parties égales : construction à la règle seule.

Télécharger la figure GéoPlan pliage_en_trois_4.g2w

2.c. Autre réseau de droites parallèles

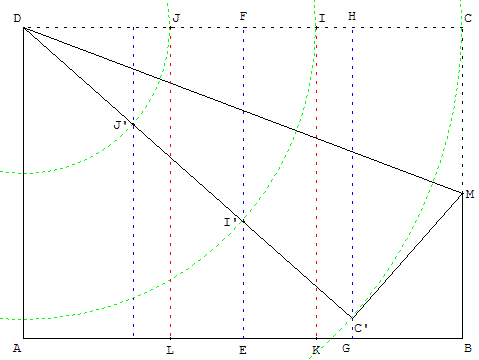
On peut utiliser les droites parallèles obtenues en pliant la feuille en quatre (la largeur étant supérieure aux deux tiers de la longueur, ce qui est le cas pour une feuille A4) :
Je plie une feuille de papier en 4 parties égales (en 2 deux fois de suite) ;
je plie l'un des bords longs depuis le coin D en amenant le coin C qui est à l'autre extrémité de ce bord sur la troisième ligne [HG] des pliages précédents.
Les deux premières lignes de pliage permettent de repérer sur le bord long deux points I’ et J’ partageant [AC’] en trois.
La feuille remise à plat, je n'ai plus qu'à plier la feuille en trois parties égales (parallèlement aux bords courts) en utilisant les deux repères I et J sur le bord long [CD].

Télécharger la figure GéoPlan pliage_en_trois_2.g2w

2.d. Droites concourantes au milieu de la demi-feuille

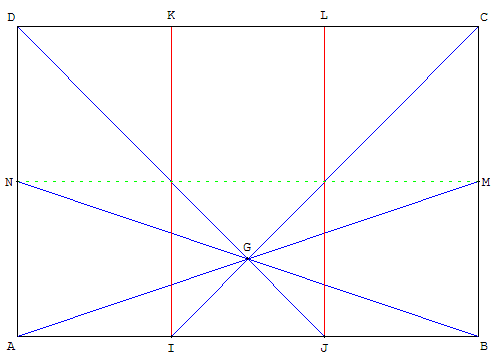
On considère une feuille rectangulaire ABCD.

La plier en deux pour obtenir les milieux N de [AD] et M de [BC].

Plier le rectangle ABMN suivant ses deux diagonales pour obtenir le point G.

Plier la feuille en marquant les droites joignant les deux autres sommets au point G.

Ces deux droites (CG) et (DG) déterminent sur l'autre bord deux points I et J, qui partagent [AB] en trois parties égales.

Télécharger la figure GéoPlan pliage_en_trois_3.g2w

Voir justification avec le barycentre

Voir aussi le partage d'un segment en trois

3.1. Partage en cinq de la diagonale d'un rectangle

Construire 1/5 par pliage

ABCD est un carré ou un rectangle (L × l), qui peut être la feuille complète.
Placer un point E au quart d'un des côtés, pour obtenir les cinquièmes de segments.

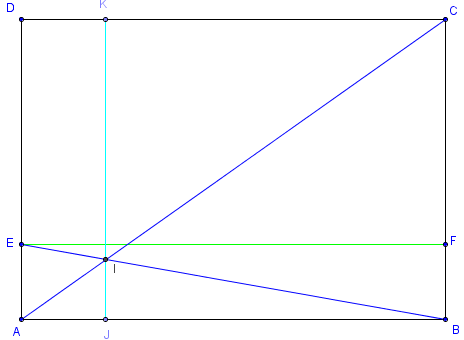
Réalisation par pliages

Avec deux pliages, parallèlement à la longueur, au milieu du côté [AD], puis au quart, on peut trouver pli [EF] et le point E.

Plier selon la diagonale [AC], puis [EB].

Les deux plis se coupent en I qui est au cinquième de la diagonale.

Il est possible de réaliser, parallèlement aux bords, un dernier pli [JK] pour le partage en cinq des côtés.

Figure interactive dans GeoGebraTube : partage en cinq de la diagonale d'un rectangle

Pour un carré, valider L = l.

Cette figure est aussi utilisée pour le partage en 3 avec e = AE = 1/2.
Elle permet de construire par pliage les nombres 1/(2^k + 1) avec AE = 1/2^k.

Il est possible de construire tous les rationnels par pliage

Étant donné un rationnel a/b, compris entre 0 et 1, on peut construire, sur la diagonale d'un carré ABCD de côté 1, un point ayant pour coordonnées ce nombre.

Pour cela, choisir une puissance de 2, n = 2^k la plus petite possible, supérieure à a et à b - a.
En pliant k fois le long du côté [AB], placer le point E, sur [AD], tel que AE = a/n, puis le point F sur [CB], tel que CF = (b - a)/n.
Le pli selon [EF] coupe la diagonale [AC] au point I de coordonnées (a/b, a/b) cherché.

Démonstration par Thalès, avec la similitude des triangles IAE et ICF :
CF/IF = AE/AI, d'où CF = AE × (1/AI) × IF = a/n × (b/a) × (1 - a/b) = (b - a)/n.

Construire 2/5 par pliage

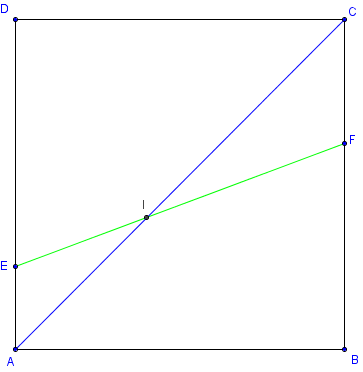
e = AE = 2/8 = 1/4 ;  f = CF = 3/8.
Les coordonnées de I sont 2/5 (ratio = 0,4).

Modifier e et f dans la figure GeoGebraTube de droite

Construire 3/10 par pliage

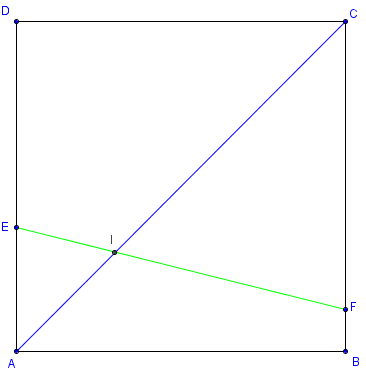
e = AE = 3/8 ;  f = CF = 7/8.
Les coordonnées de I sont 3/10 (ratio = 0,3)

Figure interactive dans GeoGebraTube : partage de la diagonale d'un rectangle

3.2. Partage aux trois onzième d'un côté d'un rectangle

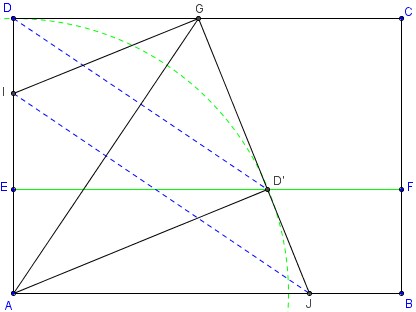
ABCD est un rectangle (L × l), qui peut être la feuille complète.
Placer un point E aux trois huitième d'un des côtés, puis avec deux pliages, obtenir un point I aux huit onzièmes de ce côté.

Réalisation par pliages

Avec trois pliages, parallèlement à la longueur, au milieu du côté [AD], puis au quart, enfin aux trois huitième de [AD], on obtient le pli [EF].

Rabattre en D’ sur [EF], le sommet D (D’ est à l'intersection de [EF] et du cercle de centre A, passant par D).
Le coin du rectangle est alors plié selon [AG] (médiatrice de [DD’]).

Replacer D et rabattre en G sur [CD], le sommet A.
Ce coin du rectangle est plié selon [IJ] (médiatrice de [AG]).

Le point I est aux trois onzième du côté [DA] à partir de D.

Figure interactive dans GeoGebraTube : partage aux trois onzième du rectangle

4. Pliage d'un rectangle selon une diagonale

ABCD est un rectangle (L × l), qui peut être la feuille complète.

En le pliant selon la diagonale [AC], on obtient le point B’ symétrique de B.

[AB’] et [CD] se coupent en I.

Si O est le centre du rectangle, que l'on obtient par un pli suivant l'autre diagonale [BD], la droite (OI), axe de symétrie de la figure, est la médiatrice de [AC].

Le triangle AIC est isocèle.

Figure interactive dans GeoGebraTube : pliage d'un rectangle selon une diagonale

5. Pliage d'un triangle selon les droites des milieux

Classe de quatrième

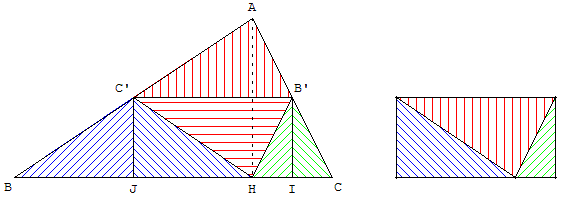
Plier un triangle ABC suivant la droite des milieux (B’C’).

Pour cela, ayant découpé le triangle ABC dans une feuille de papier, rabattre le point A en H, pied de la hauteur issue de A.

Il est possible de trouver la hauteur par pliage en faisant glisser le point C sur le segment [BC], en superposant les deux bords et en marquant le pli lorsque celui-ci passe par A.

Rabattre ensuite les points B ou C en H. On obtient un rectangle.

Dans ce rectangle on retrouve la somme des angles du triangle égale à l'angle plat IHJ, soit 180°.

L'aire du triangle est le double de l'aire de ce rectangle d'où la formule :
Aire(ABC) = 2 B’C’ × B’I = 2 × BC × AH
        = base × hauteur.

Télécharger la figure GéoPlan pliage_pliage_triangle.g2w

 Voir : triangle au collège ; aire du triangle

6. Triangle équilatéral

6.a. Construction du triangle équilatéral par pliage d'un cercle

Classe de 3^e

Comment dessiner un triangle équuilatéral par pliage d'un cercle

Dessiner un cercle et tracer deux diamètres perpendiculaires [AA’] et [DE]. Rabattre le point A’ sur O.
Le pli rencontre [AA’] en H, le cercle en B et C. Quelle est la nature du triangle ABC ?

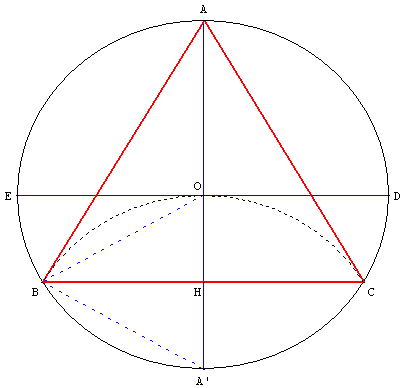
Solution

Les triangles OBA’ et OCA’, ayant leurs trois côtés de longueur égale au rayon du cercle, sont équilatéraux ; l'angle au centre BOC mesure 120°.
L'angle inscrit BAC mesure 60°. ABC est un triangle équilatéral.

Longueur du côté et aire

Si R est le rayon du cercle circonscrit,
la hauteur h du triangle est AH = AO + OH = R.

Dans le triangle rectangle ABH, le cosinus de l'angle BÂH de 30° permet de calculer
la hauteur h = a,
en simplifiant R = a,
on trouve que a, longueur du côté BC, est égal à R.

L'aire du triangle est AH × BC = 3R².

Télécharger la figure GéoPlan equi_pli.g2w

6.b. Construction d'un triangle équilatéral dans une bande

Comment dessiner un triangle équilatéral par pliage d'une bande rectangulaire

6.b.1. Triangle équilatéral de côté, la largeur de la bande

Triangle équilatéral ayant pour base la largeur de la bande, le troisième sommet sur la médiatrice de la bande.

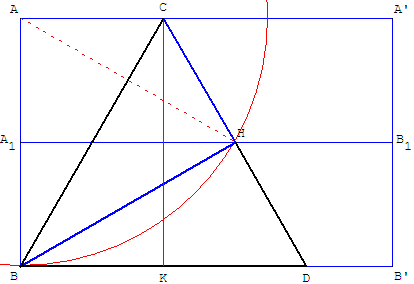
Plier une bande rectangulaire ABB’A’ de largeur a = AB suivant la médiatrice (A₁B₁) du rectangle.

Plier l'angle en B en rabattant le coin A, sur la médiatrice (A₁B₁), en C.
Le coin BAD se trouve alors en BCD.

C est équidistant de A et B, soit BC = AC = a.
Par le pliage BC = BA = a. Les trois côtés sont de même longueur.
ABC est un triangle équilatéral de côté a.

Construire le point C intersection de [A₁B₁] et du cercle de centre A, passant par B.
La médiatrice de [AC] coupe (AA’) en D.

Télécharger la figure GéoPlan bande_equi.g2w

6.b.2. Triangle équilatéral de hauteur, la hauteur de la bande

Reprise de la figure pré cédante en utilisant le pli comme côté d'un triangle équilatéral de base la longueur de la bande, le troisième côté est obtenu par prolongement à partir de son milieu.

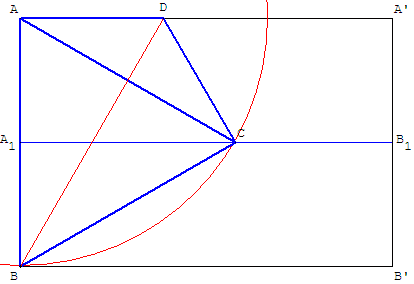
Plier une bande rectangulaire ABB’A’ de hauteur h = AB suivant la médiatrice (A₁B₁) du rectangle.

Plier l'angle en B pour amener le coin A, sur la médiatrice (A₁B₁), en H.

On obtient le pied H de la hauteur [BH] du triangle. Le pli marque le côté [BC]. Marquer enfin le pli (CH) pour obtenir le côté [CD].

H est équidistant de A et B. Par le pliage BH = BA = h. H est le milieu de [CD] du triangle équilatéral BCD de hauteur h.

Construire le point H intersection de [A₁B₁] et du cercle de centre A, passant par B.
La médiatrice de [AH] coupe (AA’) en C et la droite (CH) coupe (BB’) en D, troisième sommet du triangle équilatéral BCD.

Télécharger la figure GéoPlan bande_equi_1.g2w

6.c. Triangle équilatéral avec la règle à bords parallèles

Application : retrouver le pliage ci-dessus avec la règle à bords parallèle

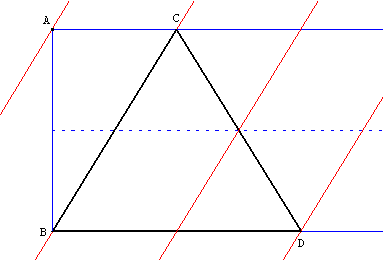
Soit une une règle à bords parallèles de la largeur l et une bande rectangulaire de largeur AB = 2l.

Il est possible de dessiner la bande en reportant deux fois la règle et en traçant trois droites parallèles espacées d'une largeur l.

Placer un bord de la règle sur le point A et l'autre bord sur le point B, ce deuxième bord coupe le rectangle en C, reporter deux fois la règle pour obtenir le point D.

Le symétrique H de A par rapport à (BC) est le milieu de [CD].
Le triangle BCD est équilatéral.

Télécharger la figure GéoPlan bande_equi_2.g2w

6.d. Patron du tétraèdre régulier

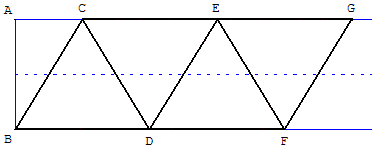
Pour construire un tétraèdre régulier avec cette bande, compléter la construction par quatre triangles équilatéraux.

Télécharger la figure GéoPlan bande_equi_3.g2w

Voir ci-dessous : construction d'un hexagone par pliage d'un triangle équilatéral

6.e.Triangle équilatéral dans une feuille carrée

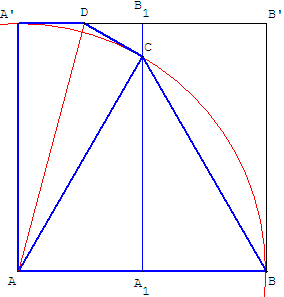
Plier une feuille carrée ABB’A’
de côté a = AB suivant la médiatrice (A₁B₁) du carré.

Pour la construction du triangle équilatéral de côté [AB] plier l'angle en A pour amener le coin A’, sur la médiatrice (A₁B₁), en C. Le coin AA’D se trouve alors en ACD.

C est équidistant de A et B,
soit AC = BC = a.
Comme AB = a. Les trois côtés sont de même longueur.
Le triangle ABC est équilatéral.

Géométrie dynamique

Construire le point C intersection de [A₁B₁] et du cercle de centre A passant par B.
La médiatrice de [A’C] coupe (A’B’) en D.

Remarque : cette construction permet de construire des angles de 60°, 30° et 15° :
BÂC = 60°, A’ÂC = 30°, DÂC = 15°.

Télécharger la figure GéoPlan carre_equi.g2w

7. Constructions du pentagone par pliage

7.a. Construction exacte par nœud d'une bande

Nœud d'or

Cet ingénieux procédé de construction du pentagone régulier se trouve indiqué sans démonstration dans un Ouvrage d'Urbano d'Aviso, publié à Rome, en 1682.

Édouard Lucas - Mathématicien français 1842-1891
L'arithmétique amusante - Adamant Media Corporation

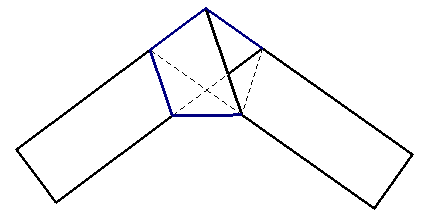
Lorsque l'on fait un nœud avec une bande rectangulaire, si l'on aplatit ce nœud en marquant les plis, la silhouette qui apparaît est celle d'un pentagone.

La construction est exacte, mais un peu difficile.

Bibliographie : Salles-Le Gac Danielle et Herrera Ruben Rodriguez

 Nouvelles pratiques de la géométrie - IREM Caen - 2008

Forum ilemaths

Je connaissais la construction avec le nœud ou le pliage d'une bande de papier, c'est comme cela que l'on fait des étoiles en pliant toute la bande plusieurs fois et en écrasant ensuite un peu les côtés.

J'ai pris deux bandes de papier mises bout à bout de 1 cm de large sur 29,7 cm de long soit une longueur totale de 59,4 cm.
C'est plus joli avec du papier de Noël !
A+, kiKo21.

Application : construction du dodécaèdre par pliage de bandes de papier

Voir aussi : constructions du pentagone avec quatre règles à bords parallèles

7.b. Pentagone approchée par pliage d'une feuille A4

Dessiner un pentagone régulier sans compas.

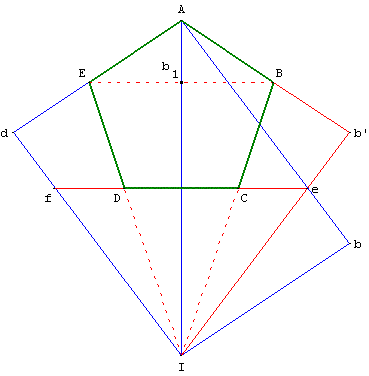
AbId est une feuille au format A4 (ou An). Ab = Ib .

[AI] étant une diagonale, replier I sur A. Le pli est le segment [ef]. Le point b se place en b’. Plier ensuite [b’e] sur la diagonale [AI] en plaçant b’ en b₁. De même, plier [df] sur la diagonale [AI] en plaçant d en b₁.

ABCD est pentagone presque régulier tel que tan IÂB = b’I/Ib’ = ce qui correspond à un angle d'environ 54,8° supérieur aux 54° degrés attendus.

Télécharger la figure GéoPlan pent_pli.g2w

8. Hexagone par pliage d'un triangle équilatéral

Ayant découpé un triangle équilatéral PQR dans une feuille de papier, amener par pliage un sommet sur l'autre pour marquer une médiatrice (par exemple, plier P sur R pour marquer QJ),
déplier, puis un deuxième pliage permet de marquer une autre médiatrice.

Les médiatrices se coupent au centre O du triangle.

Il est alors possible de réaliser un hexagone régulier en ramenant les trois sommets au centre du triangle et en pliant pour marquer les côtés [BC], [DE] et [FA].

Télécharger la figure GéoPlan hexa_dans_equi.g2w

Voir : tracer un hexagone régulier

Table des matières

Pliages dans d'autres pages du site

Pliage du coin d'une feuille - Olympiades 2004

Trisection de l'angle

Google friendly

Copyright 2003 - © Patrice Debart