Descartes et les Mathématiques

Barycentre

À la recherche du point G…

 Le barycentre n'est plus étudié au lycée.

À mes élèves de Meknès et à mon inspecteur qui, du fond de la classe, n'a guère apprécié cette leçon.

Tout ce qui est dit ici en géométrie plane s'applique dans n'importe quel plan de l'espace !

En géométrie affine, le barycentre de plusieurs points affectés de coefficients est un point réalisant une égalité vectorielle.
Le calcul de barycentre est un des outils de la géométrie affine.

1. Rappels sur les vecteurs

1.a. Parallélogramme : égalité de vecteurs et somme +  ;
vecteur opposé −  ; différence de deux vecteurs  − ; multiplication par un réel.
Représentation d'une somme de trois vecteurs dans l'espace : règle du parallélépipède.

Voir : vecteurs en seconde

1.b. Vecteurs colinéaires.

1.c. Droite passant par A de direction .

1.d. Vecteurs coplanaires.

1.e. Milieu : I milieu de [AB] : + = .

2. Repère

2.a. Droite : (A, )
2.b. Plan : (O, , )
2.c. Espace : (O, , , )

3. Barycentre de deux points

3.a. Activités

Balance romaine.

3.b. Définition et formules

Définition :

soit (A, α) et (B, β) deux points pondérés tels que α + β ≠ 0,
il existe un point unique G tel que α + β =  ;
le point G est appelé barycentre des points pondérés (A, α) et (B, β).

Pour chercher G, avec la relation de Chasles,
remplacer par + .

On obtient : (α + β) = − β ,
donc = .

Cette relation assure que le point G existe et est unique.

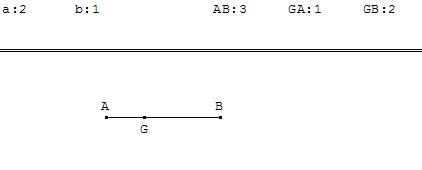
Figure : barycentre de (A, 2) ; (B, 1)

Si k ≠ 0, alors kα + kβ = ; ceci montre que le point G est aussi le barycentre des points pondérés (A, kα) et (B, kβ).

Coordonnées barycentriques d'un point sur une droite

Soit A et B deux points distincts d'une droite.
Pour tout point M de la droite, il existe un couple unique (α, β) de nombres réels tels que :
  • α + β = 1;
  • M est le barycentre des points pondérés (A, α) et (B, β).

(α, β) sont les coordonnées barycentriques de M relativement à A et B.

On perd l'unicité du couple de réels (α, β), en remplaçant la première condition par α + β ≠ 0.

Trucs et astuces GeoGebra

Le barycentre des points pondérés (A, α) et (B, β) est donné par (αA + βB)/(α + β).
Pour placer le barycentre G, il suffit de saisir G = (αA + βB)/(α + β).

Dans GeoGebra, il n'existe pas de repère sur une droite, pour y placer un point, utiliser les coordonnées barycentriques.

3.c. Position du barycentre

De la colinéarité des vecteurs et , on peut déduire que les points A, B et G sont alignés.

théorème

Le barycentre de deux points A et B appartient à la droite (AB).
Il est sur le segment [AB] si les coefficients sont de même signe,
au milieu si les coefficients sont égaux.
De A et de B, le point le plus près du barycentre est celui dont le coefficient a la plus grande valeur absolue.

Si les coefficients sont de même signe, on a 0 ≤ ≤ 1, donc le point G appartient au segment [AB].

α = − β d'où |α| GA = |β| GB, donc si |α| ≥ |β| ; GA est plus petit que GB ; G est plus près de A.

3.d. Problème réciproque

Exprimer un point comme barycentre de deux autres :

B milieu [AC] : B isobarycentre de A et de C,
A barycentre de (B, 2) et (C, −1) : 2 = ,
C barycentre de (A, 1) et (B, −2) : 2 = .

B au tiers de [AC] : B barycentre de (A, 2) et (C, 1) : 2 = ,
A barycentre de (B, 3) et (C, −1) : 3 = ,
C barycentre de (A, 2) et (B, −3) : CA = 3 ; CB = 2 d'où 3 = 2 .

3.e. Fonction vectorielle de Leibniz α 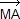+ β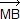

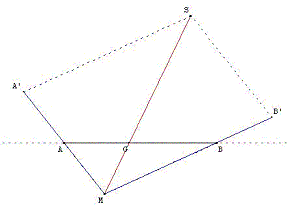
Figure : G barycentre de (A, 2) et (B, )

= α  ; = β  ;
= + = α + β .

Fonction vectorielle de Leibniz

Soit (A, α) et (B, β) deux points pondérés tels que α + β ≠ 0, et G leur barycentre.

Pour tout point M du plan, on a :

α + β = α( + ) + β( + ) =
(α + β) + α + β = (α + β) + = (α + β) .

(α + β) = α + β

= + .

En remplaçant M par G on retrouve la définition du barycentre.

En remplaçant M par A ou par B on reconnaît les formules permettant de calculer les vecteurs ou .
Dans un repère (O, , ), remplacer M par O permet d'obtenir les coordonnées du barycentre.

Montrer un alignement

Pour tout point M du plan, les propriétés suivantes sont équivalentes :
  • les points A, B et C sont alignés
  • il existe trois réels α, β et γ, non tous nuls, tels que α + β + γ = 0 et α + β + γ = .

En effet si A et B sont distincts, il existe deux réels α et β, non tous nuls, tel que C soit le barycentre de (A, α) et (B, β).
Comme (α + β) = α + β , il suffit de choisir γ = − (α + β).

3.f. Cas particuliers : coefficients égaux ou opposés

Médianes d'un triangle : si les coefficients α et β sont égaux et non nuls, l'isobarycentre I des points (A, α) et (B, β) est le milieu du segment [AB].
On choisit souvent α = β = 1 ; on a alors + = .
D'où, pour tout point M, la forme vectorielle du « théorème de la médiane » dans le triangle ABM :

+ = 2 .

En géométrie analytique ou avec le produit scalaire, on peut vérifier la somme ou la différence des carrés de deux côtés d'un triangle avec les « théorèmes de la médiane » ;
  – premier théorème de la médiane : MA² + MB² = 2 MI² + (formule d'Apollonius de Perge, 262/190 avant J.-C.).
  – troisième théorème de la médiane : MA² − MB² = 2 . ou |MA² − MB²| = 2 AB × IH ; où le point H est la projection orthogonale du point M sur la droite (AB).

Voir lieux et théorème de la médiane

Coefficients opposés : si α + β = 0 alors α + β = α( − ) = α est un vecteur constant indépendant du point M. Il n'y a pas de barycentre si A et B sont distincts.

4. Barycentre de trois points

4.a. Extension des définitions

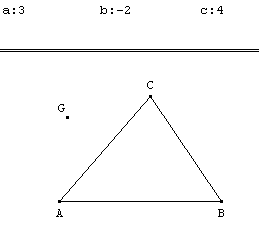
Soit (A, α) ; (B, β) et (C, γ) trois points pondérés tels que α + β + γ ≠ 0,
il existe un point unique G tel que :

α + β + γ =  ;

le point G est appelé barycentre des points pondérés (A, α) ; (B, β) et (C, γ).

Figure : Barycentre de (A, 3) ; (B, 2) et (C,4)

Démonstration : calcul du vecteur  :
α + β + γ =
α + β ( + ) + γ ( + ) =
(α + β + γ) + β + γ =
(α + β + γ) = β + γ
= +

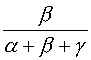
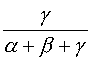
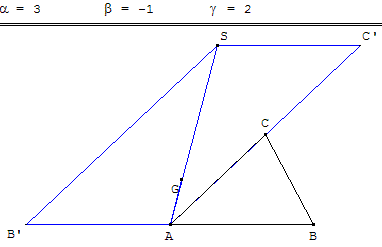
Sur la figure ci-dessus :

= β ; = γ ;

= + = β + γ

=

Coordonnées barycentriques d'un point dans un plan

Soit A, B et C trois points du plan, tous distincts et non alignés.

Théorème de Gergonne (Joseph Gergonne 1771-1859) :
Pour tout point M du plan, il existe un triplet unique (α, β, γ) de nombres réels tels que :
  • α + β + γ = 1;
  • M est le barycentre des points pondérés (A, α) ; (B, β) et (C, γ).

(α, β, γ) sont les coordonnées barycentriques de M relativement à A, B et C.

On perd l'unicité du triplet de réels (α, β, γ), en remplaçant la première condition par α + β + γ ≠ 0.

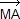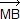4.b. Fonction vectorielle de Leibniz α + β + γ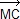

Transformation pour calculer le vecteur  :
α + β + γ = ,
α ( + ) + β ( + ) + γ ( + ) = .

Quel que soit le point M, on a :
α + β + γ = (α + β + γ)
= + + .

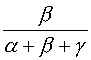
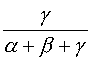
4.c. Exemples : centre de gravité d'un triangle

Exemple 1 : isobarycentre d'un triangle

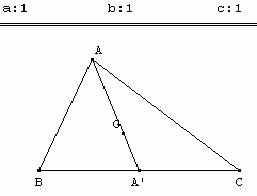
Centre de gravité d'un triangle

Soit G l'isobarycentre des sommets d'un triangle ABC.

En prenant α = β = γ = 1,
le centre de gravité G est le barycentre des trois points pondérés (A, 1) ; (B, 1) et (C, 1) ;
et on a :

+ + =

Si A’ est le milieu de [BC] on a + = 2

donc + 2 =

G est donc le barycentre de (A, 1) et (A’, 2).

G appartient à la médiane [AA’] du triangle ABC et est aux , à partir de A, de cette médiane.

La fonction de Leibniz permet d'écrire pour tout point M : + + = 3 .

Exemple 2 : calcul vectoriel

Trouver le point G barycentre de (A, 2) ; (B, 1) et (C, 1).

Choisir A comme origine des vecteurs de la fonction vectorielle de Leibniz :
4 = + = 2 où I est le milieu de [BC].
=  : G est le milieu de [AI].

Calcul vectoriel :
2 + + =
2 + 2 =

4.d. Théorème du barycentre partiel (ou d'associativité)

Règle d'associativité :

On ne change pas le barycentre de trois points pondérés en remplaçant deux d'entre eux par leur barycentre partiel (s'il existe), affecté de la somme des deux coefficients.

Exemple 1 : B’ barycentre partiel

Construction du barycentre G de (A, −1) ; (B, 2) et (C, 3) :

Pour cela, construire le barycentre B’ de (A, −1) et (C, 3),
puis conclure que G est le milieu de [BB’].

Associativité : construction de barycentres partiels

Pour trouver le barycentre G de trois points pondérés (A, α) ; (B, β) et (C, γ),
si β + γ ≠ 0 et α + γ ≠ 0, tracer le point A’, barycentre partiel de (B, β) et (C, γ) ; puis le point B’ barycentre partiel de (A, α) et (C, γ).
Le point d'intersection des droites (AA’) et (BB’) est le point G, le barycentre cherché.

Remarque : si α + β ≠ 0, la droite (CG) coupe le côté (AB) en C’, qui est le barycentre partiel de (A, α) et (B, β).

Exemple 2 : Construire les barycentres partiels

construction du barycentre de
(A, 2) ; (B, −1) et (C, 4) où BC = 6 cm ;

construire les barycentres partiels C’ de (A, 2) ; (B, −1) et A’ de (B, −1) ; (C, 4),

puis trouver G à l'intersection des droites (CC’) et (AA’).

Exemple 3 : pas de barycentre partiel sur la droite (BC)

G barycentre de (A, 2) ; (B, 1) et (C, −1). Construire les barycentres partiels B’ et C’.

Le choix de A comme origine des vecteurs de la fonction vectorielle de Leibniz permet d'écrire :

2 = − = .

Vérifier que la droite (AG) est parallèle à (BC).

Conclusions

Si β + γ ≠ 0, A’ est le barycentre partiel de (B, β) et (C, γ), alors G est le barycentre de (A, α) et (A’, β + γ).
Si α + γ ≠ 0, B’ est le barycentre partiel de (A, α) et (C, γ), alors G est le barycentre de (B, β) et (B’, α + γ).
Si α + β ≠ 0, C’ est le barycentre partiel de (A, α) et (B, β), alors G est le barycentre de (C, γ) et (C’, α + β).

Lorsqu'elles existent les droites (AA’), (BB’) et (CC’) sont concourantes en G.

4.e. Problème réciproque

Exprimer un point comme barycentre de trois autres points

Exercice 1

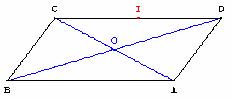
ABCD est un parallélogramme.

Écrire D comme barycentre de A, B et C :

Méthode 1 ; somme vectorielle : = + , on en déduit que − + =
D est le barycentre de (A, 1) ; (B, −1) et (C, 1).

Méthode 2 ; associativité : O centre du parallélogramme 2 =  ;
2 − = ; D est le barycentre de (O, 2) et (B, −1) ;
O est l'isobarycentre de (A, 1) et (C, 1) : 2 = + (médiane du triangle ADC).

Exercice 2

ABCD est un parallélogramme, I est le milieu de [CD].
écrire I comme barycentre de A, B et C.

Solution

I est le barycentre de (A, α) ; (B, β) et (C, γ) avec, par exemple, α = 1, β = – 1, γ = 2.

Méthode 1 : associativité : I est l'isobarycentre de C et D donc + =
Comme D est le barycentre de (A, 1) ; (B, −1) et (C, 1) on a :
= − + , d'où + ( − + ) = , soit − + 2 = .
I est le barycentre de (A, 1) ; (B, −1) et (C, 2).

Méthode 2 : calcul vectoriel : 2 = = + soit − + 2 = .

Exercice 3

Soit trois points A, B et G et le point C barycentre de (A, 1) ; (B, 1) et (G, −3).
Montrer que G est le centre de gravité du triangle ABC.

Solution

La fonction de Leibniz permet d'écrire pour tout point M : + − 3 = (1 + 1 − 3) ,
soit + + = 3.

En particulier pour le point G on : + + = . G est le centre de gravité du triangle ABC.

Exercice 4

Trois barycentres

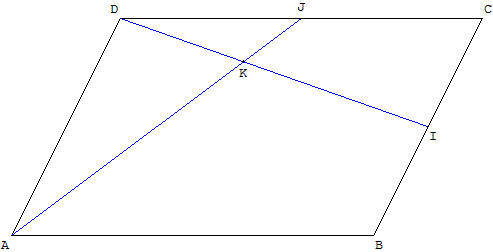
ABCD est un parallélogramme, I le milieu de [BC], J le milieu de [CD].
Les droites (AJ) et (DI) se coupent en K.

Déterminer les rapports AK/KJ ; DK/KI.

Exprimer K comme barycentre des points A, B, C, D.

Solution ci-dessous :

K est le barycentre de (A, 1) ; (B, 1) ; (C, 3) et (D, 5).

Indications

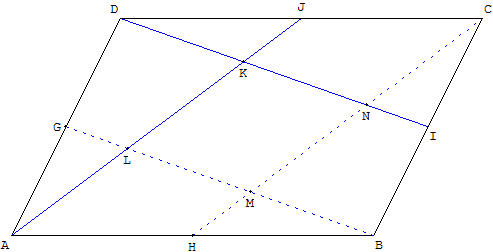
Premier barycentre
Soit G le milieu de [DA], H le milieu de [AB], L le point d'intersection de (AJ) et (BG) ; M de (BG) et (CH) ; N de (CH) et (DI).

Dans le triangle ADK, (GL) parallèle à (DI) est une droite des milieux.
L est le milieu de [AK].
LK = MN = NC; AK = 2 NC.
Dans le triangle DCN, la droite (KJ), parallèle à (CH), est une droite des milieux.
K est le milieu de [DN]. KJ = NC.
AK = 4KJ. K est le barycentre de (A, 1) ; (J, 4).
K est donc le barycentre de (A, 1) ; (C, 2) et (D, 2).

Deuxième barycentre
DK = KN = LM = MB.
Dans le triangle CBM, (NI) parallèle à (BM) est une droite des milieux.
NI = MB.
KI = KN + KN = DK.
Le rapport DK/KI est égal à .
K est donc le barycentre de (I, 2) et (D, 3).
D'où K est aussi le barycentre de (B, 1) ; (C, 1) et (D, 3).

Troisième barycentre
En ajoutant membre à membre les définitions vectorielles des barycentres précédents, on montre que :
K est le barycentre de (A, 1) ; (B, 1) ; (C, 3) et (D, 5).

4.f. Aires et barycentre

Tout point G situé à l'intérieur d'un triangle ABC peut être défini comme le barycentre des points pondérés :
[A, Aire(BCG)] ; [B, Aire(CAG)] ; [C, Aire(ABG)].

Démonstration

Si G est un point à l'intérieur d'un triangle ABC, on nomme A’ le point d'intersection de (AG) et de (BC), B’ le point d'intersection de (BG) et de (AC).

Le théorème du chevron permet de montrer que le barycentre partiel de [B, Aire(CAG)] ; [C, Aire(ABG)] est aussi celui de [B, CA’] ; [C, BA’].
Le barycentre de [B, Aire(CAG)] ; [C, Aire(ABG)] est donc situé sur la droite (AA’).

Le chevron permet de montrer, de même, que le barycentre partiel de [A, Aire(BCG)] ; [C, Aire(ABG)], qui est aussi celui de [A, CB’] ; [C, AB’], est situé sur la droite (BB’).

Par associativité, le barycentre de [A, Aire(BCG)] ; [B, Aire(CAG)] ; [C, Aire(ABG)] est situé à l'intersection des droites (AA’) et (BB’) : c'est donc le point G.

Ce résultat se généralise au cas où le point G est extérieur au triangle ABC, en comptant négativement les aires entièrement extérieures au triangle ABC.
Cela revient aussi à compter positivement les aires des triangles directs et négativement celle des triangles indirects.

Application : le centre de gravité d'un triangle le partage en trois triangles de même aire.

Sujet proposé dans le forum ilemaths

5. Problèmes d'alignement

Prouver un alignement : un point est aligné avec deux autres, s'il est le barycentre des deux points

Soit ABC un triangle, P le symétrique de B par rapport à C, Q le point défini par = et R le milieu de [AB]. Prouver que P, Q et R sont alignés.

Il suffit de montrer que Q est le barycentre de P et R :

P est le barycentre de (B, −1) et (C, 2) donc en utilisant la relation de calcul du barycentre à partir du point Q on a : = − + 2 .

R est l'isobarycentre de (A, 1) et (B, 1) et d'après la formule de la médiane du triangle QAB,
on a : 2 = + .
Q est le barycentre de (A, 1) et (C, 2) : + 2 = .

En ajoutant membre à membre les deux premières égalités vectorielles on obtient cette troisième égalité :

+ 2 = + 2 = .

Donc, Q est le barycentre de (P, 1) et (R, 2) ; P, Q et R sont alignés et QP = 2 QR.

Alignement : barycentre de deux points

Exercice 2 : le point I est aligné avec L et M, car il est le barycentre de ces deux points

Soit un triangle ABC ; I, J et K les milieux des côtés [BC], [CA] et [AB], L est le milieu de [JC] et M le symétrique de K par rapport à B.

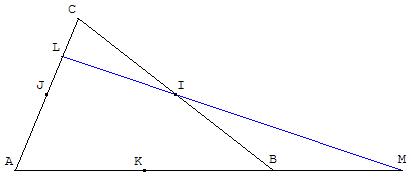
5.2.a. Écrire L comme barycentre et calculer 4 .

5.2.b. Écrire M comme barycentre et calculer 2 .

5.2.c. Écrire I comme barycentre.
          Conclure à l'alignement de I, L et M.

Solution 

5.2.a. L est le barycentre de (A, 1) et (C, 3) d'où 4 = + 3

5.2.b. M est le barycentre de (A, −1) et (B, 3) d'où 2 = − + 3

5.2.c. En ajoutant membre à membres les deux égalités précédentes,
on a : 4 + 2 = + 3 − + 3 = 3 ( + ) = .
En effet, + = car I est le milieu [BC].
Donc, 2(2 + ) = ; I est le barycentre de (L, 2) et (M, 1).

Les points I, L et M sont alignés et = 2 .

6. Problèmes de lieux

ABC est un triangle équilatéral tel que AB = 8 (l'unité est égale à 1 cm).
H est le milieu de [BC].

6.a. construire le barycentre G des points pondérés (A, 2) ; (B, 1) et (C, 1).

On a alors les relations :
4 = 2 + +

et 2 = + (MH est une médiane de MBC).

6.b. Dire quel est l'ensemble (D₁) des points M tels que
2 + + soit colinéaire à et de même sens que .

Construire (D₁).

6.c. Dire quel est l'ensemble (D₂) des points M tels que .
Construire (D₂).

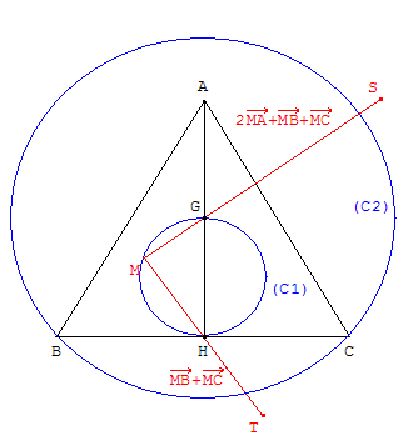
6.d. Dire quel est l'ensemble (C₁) des points M tels que :
2 + + soit orthogonal à + .

Construire (C₁).

6.e. Dire quel est l'ensemble (C₂) des points M tels que :.

Construire (C₂).

Montrer que le cercle (C₂) contient le point B.

Cercles d'Apollonius : voir lieux géométriques dans le triangle

Lieux géométriques

6.d. Somme de carrés α MA² + β MC² + γ MC²

Transformation pour calculer α MA² + β MC² + γ MC² avec le barycentre des points pondérés (A, α) ; (B, β) et (C, γ).

Utilisation du produit scalaire pour calculer des carrés.

α MA² + β MC² + γ MC² = α ² + β ² + γ ² = α( + )² + β( + )² + γ( + )²

= α MG² + 2α . + α GA² + β MG² + 2 β . + β GB² + γ MG² + 2γ . + γ GC²

= (α + β + γ) MG² + 2 . (α + β + γ ) + α GA² + β GB²+ γ GC²

Comme α + β + γ = , on a :

α MA² + β MC² + γ MC² = (α + β + γ) MG² + α GA² + β GB²+ γ GC²

Si d² > α GA² + β GB² + γ GC², le lieu des points M tel que α MA² + β MC² + γ MC² = d² est un cercle de centre G.

Applications
  – Deux points : α MA² + β MC² = (α + β) MG² + α GA² + β GB² ; voir lieux et théorème de la médiane

  – Quatre points : α MA² + β MC² + γ MC² + δ MD² = (α + β + γ + δ) MG² + α GA² + β GB²+ γ GC² + δ GD² ;
      voir le calcul de Mons. des Cartes

7. Barycentre de quatre points

7.a. Extension des définitions

Si α + β + γ + δ ≠ 0 ; le point G défini par α + β + γ + δ = est le barycentre des points pondérés (A, α) ; (B, β) ; (C, γ) et (D, δ).

Fonction vectorielle de Leibniz : pour tout point M on a : α + β + γ + δ = (α + β + γ + δ) .

= + + + .

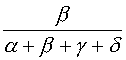
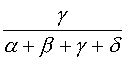
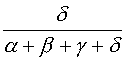
7.b. Associativité du barycentre

théorème d'associativité

On ne modifie pas le barycentre de plusieurs points si l'on regroupe certains d'entre eux, dont la somme des coefficients est non nulle, en les remplaçant par leur barycentre partiel, affecté de cette somme.

7.c. Centre de gravité d'un tétraèdre

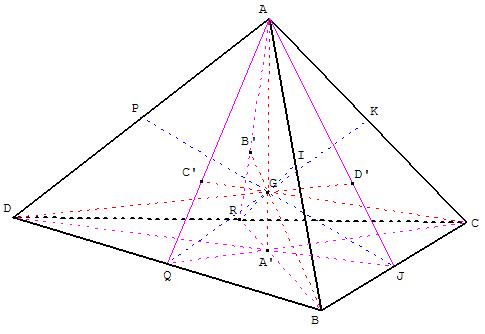
Les 4 médianes et les 3 bimédianes sont concourantes au centre de gravité du tétraèdre.

Définitions :
les médianes d'un tétraèdre sont les segments reliant les sommets au centre de gravité de la face opposée.

Les quatre médianes sont concourantes au centre de gravité du tétraèdre, situé aux , à partir du sommet, de chaque médiane.

Les bimédianes relient les milieux des arêtes opposées.

Figures 3D dans GeoGebraTube : bimédianes d'un tétraèdre

Droites concourantes

Nous trouvons 7 droites concourantes au point G, centre de gravité  :

G est le milieu des trois bimédianes [IR] ; [JP] et [KQ] qui relient les milieux d'arêtes non concourantes.

G est situé aux de chacune des médianes [AA’] ; [BB’] ; [CC’] et [DD’].

Voir ci-dessous : centre de gravité d'un quadrilatère et droites joignant les sommets d'un quadrilatère aux centres de gravité de triangles

8. Problèmes de concours et isobarycentres dans un quadrilatère

8.a. Centre de gravité d'un quadrilatère

Définition : les médianes sont les segments reliant les milieux de deux côtés opposés d'un quadrilatère

Propriétés

Les médianes d'un quadrilatère se coupent en leur milieu
qui est l'isobarycentre des sommets.

Les deux médianes et le segment joignant les milieux des diagonales sont concourants au point G, centre de gravité du quadrilatère, qui est leurs milieux.

Démonstration :

Dans un quadrilatère ABCD, soit I le milieu de [AB] et K le milieu de [CD],
G l'isobarycentre de (A, 1) ; (B, 1) ; (C, 1) ; (D,1).

D'après la règle d'associativité du barycentre,
G est le barycentre de (I, 1+1) ; (K, 1+1), d'où G est le milieu de la médiane [IK].

On montre, de même, que G est le milieu de la médiane [JL] et du segment [PQ] joignant les milieux des diagonales.

Les trois droites sont concourantes en G milieu des médianes [IK], [JL] et du segment [PQ].

Figure interactive dans GeoGebraTube : Médianes et centre de gravité d'un quadrilatère

Voir : théorème de Varignon

Remarque : ne pas confondre ce centre de gravité (isobarycentre des 4 sommets) avec le centre de masse du quadrilatère plein (centre de gravité de la surface homogène), ni avec le barycentre des côtés (centre de masse du quadrilatère en fil de fer).

4 droites joignant sommets et centres de gravité

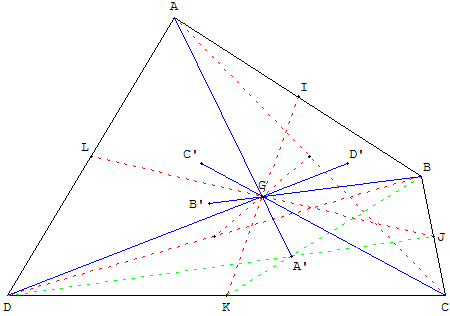
Droites joignant les sommets d'un quadrilatère aux centres de gravité de triangles

Les quatre droites joignant un sommet du quadrilatère au centre de gravité du triangle formé par les trois autres sommets sont concourantes au centre de gravité G du quadrilatère.

On a donc sept droites concourantes en G : ces quatre droites et les trois médianes étudiées au paragraphe précédent.

Visualisation dans l'espace de ce problème plan, voir : centre de gravité d'un tétraèdre

Quadrilatère formé par les centres de gravité de triangles

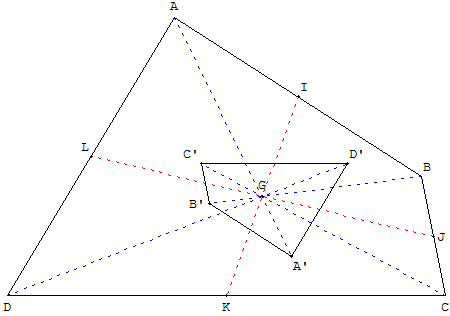
Dans le quadrilatère ABCD, de centre de gravité G, soit A’B’C’D’ le quadrilatère formé par les centres de gravité des triangles BCD, ACD, ABD, ABC.

Par exemple, d'après la règle d'associativité, G est le barycentre de (A, 1) et (A’, 3) ;
on a donc + 3 = et = − .

Ces deux quadrilatères ABCD et A’B’C’D’ sont semblables, par l'homothétie de centre G et de rapport − .

8.b. Bissectrices d'un triangle

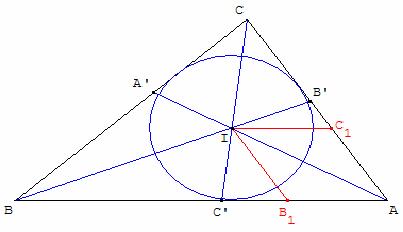
Construction du centre du cercle inscrit comme barycentre

Les trois bissectrices intérieures d'un triangle ABC sont concourantes
en I, barycentre de (A, a) ; (B, b) ; (C, c)  avec a = BC, b = AC et c = AB.

Montrer que est la somme de deux vecteurs de même norme.

D'après la définition du barycentre I, en prenant le point A pour origine on a :

(a+b+c) = b + c . Les vecteurs b et c ont la même norme bc.

Donc, = + = + .
Ces deux vecteurs ont même norme et AB₁IC₁ est un losange : la diagonale [AI] est la bissectrice de l'angle en A du triangle ABC.

Construction à la « règle et au compas », voir : problèmes de construction

8.c. Concours au centre de gravité

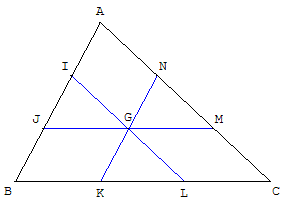
Chacun des côtés d'un triangle ABC est partagé en trois segments de même longueur ; grâce aux points : I et J sur [AB], K et L sur [BC], M et N sur [CA].
Démontrer que les droites (IL), (JM) et (KN) sont concourantes.

Solution

Pour le point G, centre de gravité du triangle, on a 2 + 2 + 2 = .

D'où 2 + + + 2 = .

I est le barycentre de (A, 2) et (B, 1) donc 2 + = 3 ,
et L est le barycentre de (B, 1) et (C,2) d'où + 2 = 3 .

Donc, 3 + 3 = .
G est le milieu de [IL]. On montre, de même, que G est le milieu de [JM] et de [KN]. G est le point de concours demandé.

Voir : Propriété de Thalès au collège

8.d. Alignement et concours

On considère un parallélogramme ABCD. K est le milieu de [AD], L le milieu de [BC] et les points I et J partagent [AB] en trois parties égales.

8.d.1. Alignement de quatre points

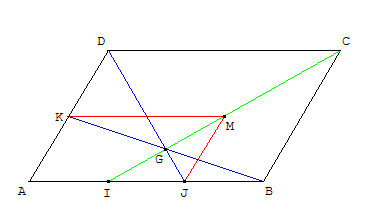
Alignement dans un parallélogramme

M est le quatrième sommet du parallélogramme JAKM.

Le but de l'exercice est de montrer que les points C, M, G et I sont alignés.

8.d.1.a. Exprimer I, J, K, M et C comme barycentre des points A, B et D.
8.d.1.b. Montrer que les droites (BK), (DJ) et (CI) sont concourantes au point G barycentre de (A, 1), (B, 2) et (D, 1).
8.d.1.c. Conclure en montrant que G et M sont des barycentres de I et C.

8.d.2. Point de concours

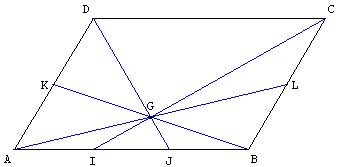
Point de concours dans un parallélogramme

Le but de l'exercice est de montrer que les droites (AL), (BK), (CI) et (DJ) sont concourantes.

8.d.2.a. Exprimer J et K comme barycentre de deux points puis exprimer G comme barycentre de A, B et D.
8.d.2.b. Exprimer C comme barycentre de A, B et D puis I comme barycentre de A et B.
8.d.2.c. Sachant que G est le barycentre de A, B et C ; calculer le vecteur 4 , en déduire que :
2 = + = et conclure.

8.d.3. Correction de l'exemple ci-dessus

8.d.2.a. Soit G le point d'intersection de (BK) et (DJ). Cherchons trois nombres α, β et δ tels que G soit le barycentre de (A, α) ; (B, β) et (D, δ). Étudions les barycentres partiels :
J est le barycentre de (A, 1) et (B, 2) donc β = 2 α et 3 = + 2 .
K est le milieu de [AD] donc α = δ et 2 = + .
En choisissant α = 1, montrons que G est le barycentre de (A, 1) ; (B, 2) et (D, 1).
En effet, en ajoutant aux deux membres de la première égalité on a :
3 + = + 2 +  ; ce vecteur a pour direction (DJ).

De même, en ajoutant 2 aux deux membres de la deuxième égalité on a :
2 + 2 = + 2 +  ; ce vecteur a pour direction (BK).
Le vecteur + 2 + , porté par deux directions distinctes, est le vecteur nul.

La règle d'associativité permet de conclure que G est l'intersection des droites (DJ) et (BK).

8.d.3.b. D'après la formule des sommets d'un parallélogramme, C est le barycentre de(A, −1) ; (B, 1) ; (D, 1),
donc en choisissant G comme origine on a : = − + + .
I est le barycentre de (A, 2) et (B, 1) donc 3 = 2 + .
En ajoutant ces deux égalités : + 3 = + 2 + = .

G est le barycentre de (C, 1) et (I, 3). Ces trois points sont alignés et G est sur la droite (CI).

8.d.2.c. En combinant les deux relations précédentes, on trouve :
+ 3 = + (2 + ) = d'où G est le barycentre de (A, 2) ; (B, 1) ; (C, 1).
En utilisant A comme origine : 4 = + . D'après la forme vectorielle du théorème de la médiane dans le triangle ABC on a :
+ = 2 .
Donc, 2 = . G est le milieu de [AL]. La droite (AL) est concourante en G, avec les trois autres droites.

Voir aussi le partage d'un segment en trois : constructions élémentaires,   règle à bords parallèles

Cas particulier du rectangle - pliage d'une feuille en trois parties égales : constructions - pliages