Petits programmes TI-92

Descartes et les Mathématiques TI-92 - Petits programmes Calcul formel et programmation au lycée - Identité de Bézout - Calcul de π, de e, de racine de 2.
Sommaire I. PGCD Identité de Bézout II. Équation du troisième degré III. Barycentre IV. Triangle	V. Calcul de 600 décimales de e VI. Calcul de 300 décimales de VII. Calcul de 600 décimales de π VIII. Fractions égyptiennes
Voici quelques algorithmes classiques pouvant faire l'objet de l'enseignement informatique. Leur écriture demande autant de compétences informatiques que mathématiques et leur programmation nécessite une grande rigueur. Ces programmes, pour l'essentiel réalisés au Club Calculatrice du Lycée Français du Caire de 1994 à 1998, ont surtout un intérêt pédagogique au moment de leur conception. Ils peuvent aussi rendre service à l'occasion d'un cours ou d'un devoir.
I. PGCD - identité de Bézout
Les fonctions pgcd(a,b) et ppcm(a,b) {version anglaise gcd(a,b) et lcm(a,b)} de la calculatrice donnent directement le pgcd et le ppcm de deux nombres a et b. En utilisant le fait que la calculatrice simplifie un quotient d'entiers 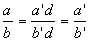. On trouve b’ avec la fonction dénom (getnum en anglais) :b’ = dénom(a/b) On a donc pgcd(a,b) = et ppcm(a,b) = . Créer la fonction permettant de calculer d en divisant b par b’ et celle calculant le ppcm en multipliant b’par a.
:pgdc(a,b) :Func :b/dénom(a/b) :End Func	:ppmc(a,b) :Func :a*dénom(a/b) :End Func
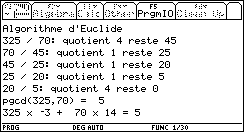
	À partir de la fonction pgcd étendu de Jean-Michel Ferrand (Les programmes TI-92, Dunod 1996) voici le programme pgcd(a,b) qui, à partir des divisions de l'algorithme d'Euclide, permet de trouver le pgcd de deux nombres a et b, puis donne le résultat de l'identité de Bézout.
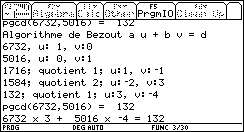
	Le programme bezout(a,b) reprend le programme pgcd et ajoute un deuxième écran donnant les coefficients u et v permettant d'exprimer les divers restes.
L'élève devant rédiger l'algorithme devra reprendre les égalités obtenues : (le programme reste à faire !) 6732 =6732 × 1 + 5016 × 0 ligne d'initialisation de l'algorithme pour a. 5016 = 6732 × 0 + 5016 × 1 idem pour b. 1716 = 6732 × 1+ 5106 × (–1) on commence, 1584 = 1716 × (–2) + 5016 =6732 × (–2) + 5106 × 3 on écrit le reste et on remplace à droite l'ancien reste 1716 par le résultat de la ligne précédente. 132 = 1584 × (–1) + 1716 = 6732 × 3 + 5106 × (–4) on remplace les deux restes par leurs valeurs trouvées dans les deux lignes précédentes. On trouve enfin l'identité.
II. Équation du troisième degré
	Le programme equa3(p(x)) permet d'expliquer comment trouver les solutions d'une équation du troisième degré p(x) = 0 ayant une solution évidente égale entière dont la valeur absolue n'est pas trop grande (la variable maxi=10 dans le programme joint permet de trouver les solutions entre –9 et 9).
Equa3 utilise le sous-programme divEucli(p(x),q(x)) qui pose la division euclidienne d'un polynôme du troisième degré par un binôme du premier degré.

III. Barycentre
Ces programmes calculent et tracent le barycentre G de trois points (A, α), (B, β) et (C, γ). Ils utilisent les trois barycentres partiels : A’ barycentre de (B, β) et (C, γ) ; B’ barycentre de (A,α) et (C, γ) ; enfin C’ barycentre de (A, α) et (B, β) Cet ensemble se compose de trois modules bary1, bary2, barytxt et du sous-programmes calbary, nompoint, orthonor, wind et initwind. Les coordonnées des points sont stockées dans la matrice b et les coefficients dans la liste c.
	bary1(xa,ya,xb,yb,xa,yc,α,β,γ) utilise les six coordonnées des points A, B et C et les trois coefficients α, β et γ. barytxt() permet ensuite de connaître les coordonnées du barycentre G et des barycentres partiels A’, B’ et C’. Le programme bary2() permet de saisir les points directement dans l'écran graphique en se déplaçant avec les flèches de direction.

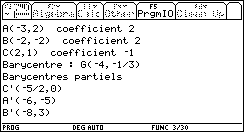
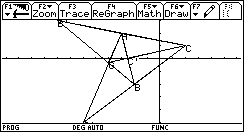
Application : pour trouver le centre de gravité d'un triangle choisir α = β = γ = 1. Le barycentre
IV. Triangle
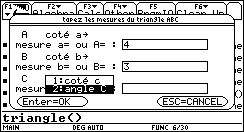
	Ce programme permet de calculer les longueurs des côtés et les angles d'un triangle. Choisir les trois longueurs des côtés ou deux côtés et un angle, ou enfin un côté et deux angles. Comme résultats, nous obtenons les trois longueurs des côtés et les trois angles en degré.

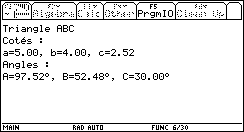
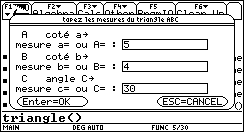
Nous obtenons, comme résultats, les trois longueurs des côtés et les trois angles en degré. Les longueurs a, b, c et les angles α, β, γ sont conservés comme variables globales. Il est possible d'effacer ces variables par programme en supprimant dans le listing l'@ de :@DelVar a, b, c, α, β, γ pour valider la ligne :DelVar a, b, c, α, β, γ (SupVar en version française)
V. Calcul de 600 décimales de e
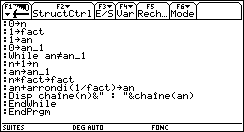
Le calcul de e par la série a_n = converge rapidement vers e. On sait que cette suite a_n est croissante et majorée par e. La suite b_n = a_n + est décroissante et minorée par e, d'où a_n est une valeur approchée par défaut de e à près. En 14 calculs le programme ci-contre donne les 11 premières décimales : e ≈ ≈ 2,71828 18284 6 En effet, 14 est le premier entier tel n que < 10^{− 11}. Le programme calcule tant que a_n est différent de a_n−1 (au sens de la machine). Pour accélérer les calculs, la factorielle est obtenue par récurrence. La TI-92 n'utilisant « que » 12 chiffres pour les calculs sur les réels pour trouver plus de décimales, une astuce est d'utiliser des nombres entiers ce qui peut nous permettre de calculer jusqu'à 600 décimales. En effet, avec la TI-92 les calculs sur les entiers sont exacts jusqu'à 10⁶¹⁴. Pour trouver p décimales de e il suffit de multiplier par 10^p et de calculer les entiers 10^p e ≈ 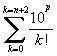avec n.n! > 10^p. Le calcul continue jusqu'à ce que la partie entière de soit nulle. On obtient ainsi le nombre entier de 614 chiffres : 2 71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274 27466 39193 20030 59921 81741 35966 29043 57290 03342 95260 59563 07381 32328 62794 34907 63233 82988 07531 95251 01901 15738 34187 93070 21540 89149 93488 41675 09244 76146 06680 82264 80016 84774 11853 74234 54424 37107 53907 77449 92069 55170 27618 38606 26133 13845 83000 75204 49338 26560 29760 67371 13200 70932 87091 27443 74704 72306 96977 20931 01416 92836 81902 55151 08657 46377 21112 52389 78442 50569 53696 77078 54499 69967 94686 44549 05987 93163 68892 30098 79312 77361 78215 42499 92295 76351 48220 82698 95193 66803 31825 28869 39849 64651 05820 93923 98294 88793 32036 25094 43117 29353 40688 510 Le calcul nécessite 299 additions d'entiers dont 296 sont des arrondis de fractions. Les trois dernières décimales sont donc comprises entre 510 – 214 = 214 et 510 + 296 = 806. Sachant que a₂₉₉ < e < b₂₉₉ les dernières décimales de e sont donc comprises entre 214 et 807. On a donc calculé e avec 610 décimales : e ≈ 2,71828…40688.
VI. Calcul de 300 décimales de 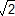. Algorithme de Babylone
La racine carrée de deux, notée (ou parfois 2^1/2), est définie comme le nombre réel positif qui multiplié par lui-même, donne le nombre 2. Riche de quatre mille ans d'histoire, carrefour entre la géométrie, l'algèbre, l'analyse ou encore la théorie des nombres, la constante de Pythagore est l'un des nombres les plus extraordinaires qui soit. Le calcul d’une valeur approchée de a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d’extraction de racines carrées. Constante fondamentale des mathématiques, ses multiples propriétés en font un objet de choix pour des applications de toutes sortes, de la détermination des formats de nos feuilles de papier aux considérations esthétiques d'architectes (Conférence SMF). 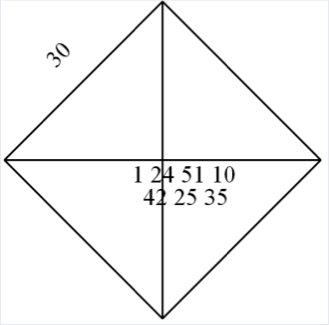Tablette babylonienne - 1000 ans avant Pythagore D'après WikiPédia et Irem de Marseille La tablette d'argile YBC 7289 est une pièce écrite en cunéiforme. Elle est datée des années 1700 avant J.-C. Elle provient sans doute du sud de l'Irak. C'est la plus ancienne représentation connue d'une valeur approchée de la racine carrée de deux. Sur le côté du carré, en haut à gauche, la mesure est 30, qui représente en base 60. Sur la diagonale horizontale, on peut lire 1 24 51 10, soit l'approximation en numération babylonienne base 60, de la forme : 1 + 24/60 + 51/60² + 10/60³. Cette écriture est égale à environ 1,414 212 9 ; elle correspond à la meilleure approximation possible de avec quatre chiffres significatifs en base 60. Elle est précise au millionième près. Sous cette inscription, la tablette donne en base 60 la forme : 42 25 35, soit 0 + 42/60 + 25/60² + 35/60³ ≈ 0,707 106 5 ; au lieu de 0,707 106 8, approximation décimale de , longueur de la diagonaledu carré.


Méthode babylonienne La « méthode de Babylone » est aussi appelée « méthode de Héron » ou « algorithme de Héron d'Alexandrie » (I^er siècle).
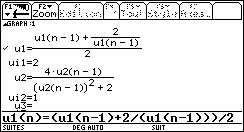
	Il y a 4000 ans les Sumériens connaissaient déjà un processus itératif, qui permettait de calculer à partir de c. On choisit a₀ (souvent 1) et on calcule la suite (a_n) par la formule de récurrence : .
	Cette suite à partir de a₁ est décroissante et minorée par . La fonction itérative de Newton, correspondant à cette suite, est f(x) = qui admet comme point fixe .
On remarque que la suite b_n = est une suite croissante à partir de b₁ et majorée par.
	Le calcul par récurrence de b_n donne : . La fonction itérative correspondant à cette suite est g(x) = qui admet comme point fixe .
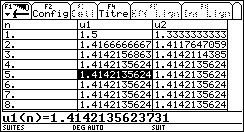
	Or b₁ < b₂ < … < b_n < < a_n < … < a₁ avec . La convergence est donc très rapide. Les calculs se font facilement dans l'écran ¨Table ou avec les fonctions racine en simple ou multiprécision.

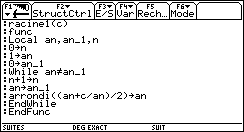
Toutes les décimales sont exactes et on obtient les résultats suivants pour .

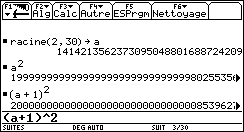
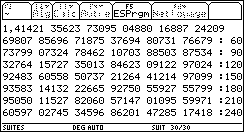
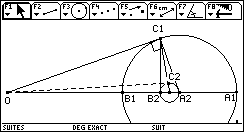
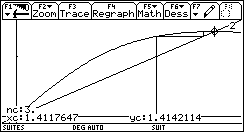
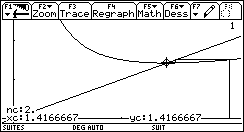
Calcul de la rapidité de convergence La représentation géométrique permet d'expliquer la convergence vers a été faite pour les triangles A₁B₁C₁ et A₂B₂C₂ avec a₁=2, d'où a₂ = 1,5 et b₁ =1. La différence de taille de ces triangles donne une idée de la convergence. Soit A_i et B_i les points d'abscisses a_i et b_i sachant que a_ib_i = c. Le cercle de diamètre A_iB_i est centré en A_i+1 d'abscisses b_i+1. Une des tangentes à ce cercle, issue de O, coupe le cercle en C_i. Dans le triangle rectangle OA_i+1C_i le pied de la Hauteur H issue de C_i est tel que : OH × OA_i+1 = OC_i². or OC_i² = OA_i × OB_i = a_ib_i = c ; puissance d'un point par rapport à un cercle, se calcule aussi avec le théorème de Pythagore. On a donc OH . a_i+1 = c ; OH est donc égal à b_i+1. Le pied de la hauteur est donc le point B_i+1. Les triangles rectangles OA_i+1C_i et A_i+1B_i+1C_i sont semblables donc : d'où en remplaçant le rayon A_i+1C_i par le diamètre A_iB_i. Or OA_i+1 < , on en déduit Pour c > 1 on a . Si à un étape du calcul on a une valeur approchée à 10^{− n} près, à l'étape suivante on aura un encadrement inférieur à 10^{− 2n}. Ainsi, à chaque itération on double le nombre de décimales justes. La convergence est donc très rapide : le calcul de 100 décimales de se fait avec 8 itérations à partir de a₁ = 2 et en seulement 3 itérations si l'on part de la valeur approchée a₁ = 1,414 213 562 37 calculée par la machine. Problème connexe avec les travaux de l'ingénieur allemand Walter Porstmann, qui a établi en 1922 le rapport de la longueur à la largeur de la feuille A4 à : un devoir qui ne fait pas un pli ! (pliage du coin d'une feuille)
VII. Calcul de 600 décimales de π Calculs de pi Les anciens Hébreu utilisaient la valeur 3 dans la Bible : … Elle avait dix coudées d'un bord à l'autre, une forme entièrement ronde … et une circonférence que mesurait un cordon de 30 coudées. (Premier livre des rois VII, 23). Dans l'ancienne Égypte, le papyrus de Rhind notait la valeur .
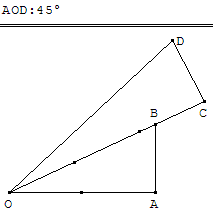
Arc tan Au XVIII^e, de nombreux calculs utilisent la fonction Arc tan, réciproque de tangente, sachant que : Arc tan 1 = et que . En 1776 l'écossais James Hutton a découvert la formule : = Arc tan + Arc tan comme la figure ci-contre montre l'angle avec OA = 2, AB = 1, OC = 3 et CD = 1. Télécharger la figure GéoPlan arctan45.g2w
La formule de John Machin = Arc tan + Arc tan permit dès 1706 le calcul de 100 décimales sans calculatrice. Sur TI-92 il suffit de programmer la fonction permettant de calculer Arc tan :

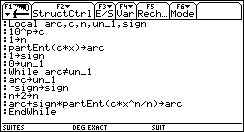
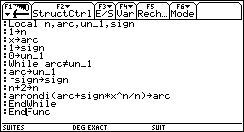
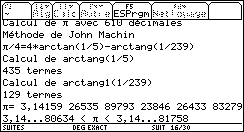
	On obtient alors 607 décimales de π exactes (en 25 minutes de calculs).
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277 05392 17176 29317 67523 84674 81846 76694 05132 00056 81 Bibliographie : Mathématiques élémentaires d'un point de vue algorithmique - Arthur Engel - Cedic 1979 Numéro spécial π - le petit Archimède - Association pour le Développement de la Culture Scientifique (ADCS) - 1980 (réédité en 1992) Publimath : Le fascinant nombre π - Jean-Paul Delahaye - Pour la science, 1997
VIII. Fractions égyptiennes Algorithme glouton de Fibonacci En 1201, Fibonacci prouva que tout nombre rationnel, compris entre 0 et 1, pouvait s'écrire sous la forme d'une somme de fractions à numérateur unitaire et proposa la méthode suivante (pour toute fraction distincte de ) : « Soustraire à la fraction donnée la plus grande fraction égyptienne possible, répéter l'opération avec la nouvelle fraction, et ainsi de suite jusqu'à ce que l'opération donne une fraction égyptienne. » Cet algorithme permet l'obtention des dénominateurs n de la décomposition de : Il suffit, si p > 1, de calculer la partie entière n de + 1, puis de calculer - , et de recommencer, avec cette dernière fraction, jusqu'à ce que le numérateur soit égal à 1. Programme pour la TI-92 La TI-92 permet de faire les calculs directement dans le mode fractionnaire exact, la simplification des fractions se faisant automatiquement. Il est aussi possible de rédiger l'algorithme dans l'éditeur de programmes :
EGYPT(x) Prgm Local p,q,f,n ClrIO Disp x getNum(x) → p While p>1 getDenom(x) → q	If mod(q,p)=0 Then q/p → n Else int(q/p)+1 → n EndIf Disp 1/n x-1/n → x getNum(x) → p EndWhile Disp x EndPrgm
Puis exécuter le programme en tapant dans la fenêtre ¨Home : Egypt(7/17) On obtient : = + + ; mais on a aussi = + + . Taper sur la touche F5 ou sur ¨Home pour sortir du programme.	$ecran calculatrice TI-92 - décomposition de 7/17 en fraction égyptienne$
4. Conjecture de Sierpinski Une conjecture de Sierpinski énonce que toute fraction irréductible de numérateur 5 a une décomposition de longueur 3. Algorithme Pour n fixé, choisir a égal à la partie entière de . Calculer de 1 en 1 les valeurs de b jusqu'à trouver que le nombre soit l'inverse d'un entier. En cas d'échec recommencer en augmentant a de 1. Le plus efficace est de calculer de -1 en -1 pour b à partir de la partie entière de jusqu'à a
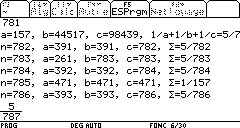
	Il semble que l'on ne sache pas encore démontrer cette conjecture. La TI-92, en une journée, sait la vérifier jusqu'à n = 1000.
Programme TI-92+, version française
Sierpin(n) Prgm drap → 0 5/n → x numér(x) → p dénom(x) → q If p=1 then q → a else ent(q/p) → a endif x-1/a → y numér(y) → p dénom(y) → q If p=1 then 2q → b 2q → c 2 → drap endif If p=2 then q → b q → c 2 → drap endif If drap=2 then disp a, b, c else ent(2/y)+1 → b	while drap<1 b+1 → b if b≤a then a+1 → a x-1/a → y ent(2/y) → b disp x a endif y-1/b → z if numér(z)=1 then dénom(z) → c 1 → drap disp a, b, c endif if 3/a<x then disp “pas de solution” pause 3 → drap endif endwhile endif endPrgm
Table des matières Google friendly	Téléchargement Télécharger ti92prog_fr.zip : les programmes TI-92 plus (ZIP version française) Télécharger ti92prog_an.zip : les programmes TI-92 et TI-92 plus (ZIP version anglaise) Télécharger ti92prog.doc : ce document au format « .doc » (176 ko) Télécharger ti92prog.pdf : ce document au format « .pdf » d'Acrobat (244 ko) Google considère l'URL originale comme une erreur de type "soft 404".
Les suites en S ou ES Immerger une bille	Problèmes de la géométrie grecque Calculatrice TI-92 : Index
	Page n^o 6, réalisée le 10/12/2000 mise à jour le 13/7/2018

TI-92 - Petits programmes

Sommaire

I. PGCD - identité de Bézout

II. Équation du troisième degré

III. Barycentre

IV. Triangle

V. Calcul de 600 décimales de e

VI. Calcul de 300 décimales de . Algorithme de Babylone

Tablette babylonienne - 1000 ans avant Pythagore

Méthode babylonienne

Calcul de la rapidité de convergence

VII. Calcul de 600 décimales de π

Calculs de pi

Arc tan

La formule de John Machin

VIII. Fractions égyptiennes

Algorithme glouton de Fibonacci

Programme pour la TI-92

4. Conjecture de Sierpinski

Algorithme

Table des matières