Descartes et les Mathématiques
Les grands problèmes de la géométrie grecque
Nombres constructibles, quadrature, duplication
Les géomètres grecs n'avaient pas GéoPlan, ni GeoGebra…
Sommaire
1. Points et nombres constructible
2. Quadrature du cercle
Calcul de π dans le papyrus de Rhind
Lunules d'Hippocrat
Le troisième grand problème de la géométrie grecque :
1. Points et nombres constructibles
Point constructible
Définition : un point est constructible à partir d'un ensemble E si je peux le construire d'une façon précise à partir de E, à la règle non graduée et au compas.
Plus précisément l'ensemble E1 des éléments constructibles, en une étape, à partir d'un ensemble E est formé par :
• les points de E,
• les points d'intersection des droites distinctes, passant par deux points distincts de E,
• les points d'intersection des cercles distincts de centre un point de E, passant par un autre point de E,
• les points d'intersection des droites et des cercles définis ci-dessus.
De même, E2 est l'ensemble des éléments constructibles en une étape à partir de E1, E3 à partir de E2, et ainsi de suite.
Définition : un point M est constructible à partir de E, s'il existe un i tel que M appartienne à Ei (on peut construire M en i étapes).
Définition : on appelle point constructible du plan (euclidien), tout point constructible à partir de E = {O, I} où OI =1.
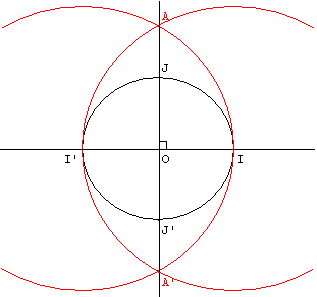
Application : montrons que le point J(0, 1) est constructible avec la construction de la médiatrice d'Œnopide de Chios (Ve siècle avant J.-C.) :
E1 contient le point I’, intersection de la droite (OI) et du cercle de centre O, passant par I.
E2 contient les points A et A’, intersections du cercle de centre I, passant par I’, et du cercle de centre I’, passant par I.
La médiatrice (AA’) de [II’] coupe le cercle de centre O, passant par I en J et J’, points de E3.
(O ; I ; J) est un repère orthonormé constructible du plan euclidien.
Télécharger la figure GéoPlan repere_oij.g2w
Définition : on appelle nombre constructible la longueur associée à deux points constructibles.
Propriétés :
Dans le plan euclidien, muni d'un repère orthonormé (O ; I ; J), toute coordonnée d'un point constructible est un nombre constructible ;
un point M(a, b) est constructible si et seulement si a et b sont des nombres constructibles.
Remarque : on parle aussi de « nombre constructible à la règle et au compas ».
Vérification
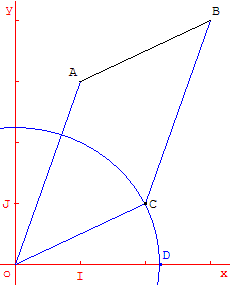
Si A et B sont deux points constructibles, alors la distance AB est un nombre constructible.
Indications :
Le point C, quatrième sommet du parallélogramme OABC, est constructible.
Le point D est constructible avec OD = OC = AB = d.
Le nombre d, abscisse d'un point constructible, est constructible.
La longueur AB est bien un nombre constructible.
Télécharger la figure GéoPlan distance_ab.g2w
La somme de deux nombres constructibles est constructible
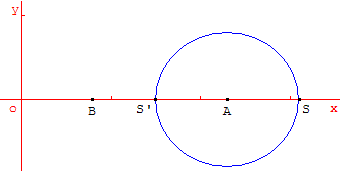
Soit a et b deux nombres constructibles ; A et B les points constructibles d'abscisses a et b.
En traçant le cercle centre A et de rayon b le nombre a+b correspond au point constructible S si a est positif ;
au point S’ s'il est négatif. a+b est donc constructible
L'opposé d'un nombre constructible est constructible
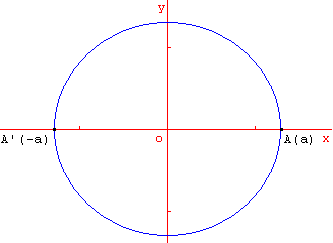
Le produit de deux nombres constructibles est constructible
Voir : la démonstration par l'application du théorème de Thalès dans la Géométrie de Descartes
ou la page construction de réels en seconde.
L'inverse d'un nombre constructible non nul est constructible.
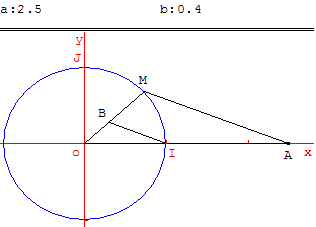
Le point A a pour abscisse a non nulle.
M est un point du cercle non situé sur Ox.
La parallèle à (AM) menée par I coupe (OM) en B.
Le point B est constructible et sur la droite repérée (O, M) a pour abscisse 1/a.
1/a est un nombre constructible.
Télécharger la figure GéoPlan inverse.g2w
Le quotient d'un nombre constructible par un nombre constructible non nul est constructible.
Voir : nombre a/b dans la page construction de réels en seconde.
La racine carrée d'un nombre constructible positif est constructible.
Voir : construction d'Euclide reprise par Descartes dans l'article construction de réels en seconde.
Nombre algébrique
Rappel : un nombre est algébrique sur un corps K s'il existe un polynôme non nul, à coefficient dans K, s'annulant sur ce nombre.
Sur Q un nombre algébrique est solution d'une équation à coefficients entiers.
Pierre-Laurent Wantzel, mathématicien français, a montré en 1837 qu'un nombre constructible est algébrique sur Q et son degré est une puissance de 2.
La réciproque est très utile pour montrer qu'un nombre n'est pas constructible.
Polygones constructibles
Théorème : un polygone régulier de n côtés est constructible si cos 
est un nombre constructible.
Pour n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20… les polygones à n côtés sont constructibles. Pour n = 7, 9, 11, 13, 14, 18, 19… ils ne le sont pas.
2. Quadrature du cercle
La quadrature du cercle : tracer, à la « règle et au compas », un carré de même aire qu'un cercle donné.
La quadrature du cercle nécessite la construction à la « règle et au compas » d'un segment de longueur la racine carrée de π.
Ce problème n'est pas résoluble, car en raison de la transcendance, π n'est pas constructible.
WikiPédia : quadratrice de Dinostrate.
Calcul de π dans l'ancienne Égypte
Le papyrus mathématique égyptien le mieux conservé est le papyrus Rhind, écrit par le scribe Ahmés vers 1650 avant J.-C. ;
Rhind est le nom du premier propriétaire Écossais qui l'acheta à Louxor en 1857.
Parmi quatre-vingt-sept problèmes, accompagnés de leurs solutions, on trouve la règle suivante pour la quadrature du cercle :
pour « construire un carré équivalant à un cercle… retirer 
au diamètre et construire le carré sur ce qui reste ».
Justifications
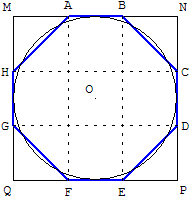
L'aire du disque de diamètre 1 est 
.
Cette aire du disque est voisine de celle de l'octogone ABCDEFGH (non régulier).
Son aire, composée de cinq carrés et quatre demi-carrés,
est égale à 7 carrés soit 7 × 
= 
.
Ce nombre est voisin du carré 
, aire du carré de côté 
: (1 − )2 = .
Les « anciens Égyptiens » utilisaient donc pour π la valeur de 4 × (1 − )2 = 
≈ 3,16, avec une incertitude
relative de 
pour le calcul de π.
Télécharger les
figures GéoPlan pi_rhind.g2w ou pi_rhind_2.g2w
Calcul de π : ti-92
Lunules d'Hippocrate
Définition : une lunule est une portion de surface délimitée par deux cercles non concentriques de rayons différents,
formant un croissant de lune en forme de ménisque : convexe d'un côté et concave de l'autre.
Les quatre lunules
Au Ve siècle avant J.-C. Hippocrate de Chios est le premier à s'être intéressé aux quadratures.
Il n'a pas réussi pour le cercle, mais il prouva la « quadrature » des lunules.
Les quatre lunules hachurées en bleu sont les surfaces comprises entre le cercle de rayon r circonscrit au carré ABCD
et les demi-cercles ayant pour diamètre d les côtés du carré :
l'aire du carré ABCD est égale à la somme des quatre aires des lunules.
Léonard de Vinci généralisera cette propriété à d'autres lunules construites sur des figures diverses.
Preuve
Le secteur circulaire OAB a une une égale au quart de l'aire du cercle de rayon r = OA,
soit 
πr2 = π(d
)2 = 
.
Cette surface est faite du triangle OAB et du segment circulaire AB.
Le demi-cercle de diamètre d = AB a une aire égale à 
π(
)2 = . Cette surface est faite d'une lunule et du segment circulaire.
Ces deux aires sont égales. Quand on leur retranche l'aire du segment circulaire, on trouve bien que l'aire de l'aire de la lunule est égale à celle du triangle OAB, soit le quart de l'aire du carré.
Télécharger la figure GéoPlan lunule_h4.g2w
Quadrature de la parabole par Archimède : analyse en 1L
3. Duplication du carré et du cube
Duplication du carré : tracer à la « règle et au compas » un carré d'aire double d'un carré donné.
Construction avec une diagonale
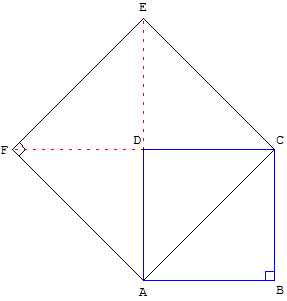
Dans Ménon, un dialogue de Platon, Socrate explique la construction ci-dessus à un jeune esclave.
La diagonale du « petit carré » le partage en deux triangles isocèles rectangles.
Le « grand carré » est formé de quatre triangles isocèles rectangles, de même aire.
Le rapport des aires des carrés est 2,
Le rapport des côtés est 
.
Remarque : la similitude directe, de centre A, d'angle 45° et de rapport , transforme le carré ABCD en le carré ACEF.
Télécharger la figure GéoPlan duplication_carre.g2w
Carrés de Léonard de Vinci
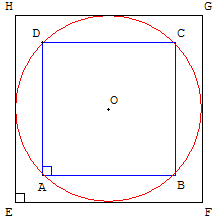
Le carré circonscrit à un cercle a une aire double de celle du carré inscrit dans ce cercle.
Télécharger la figure GéoPlan carres_vinci.g2w
Solution de Léonard de Vinci
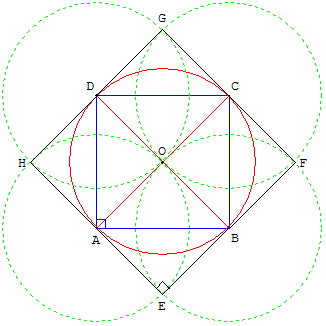
À partir d'un « petit carré » ABCD, de centre O, on trace les cercles centrés sur les sommets, passant par O.
Ces cercles se coupent en E, F, G, H, symétriques de O par rapport aux côtés du petit carré.
EFGH est un « grand carré » tangent au cercle circonscrit à ABCD.
Les diagonales du « petit carré » le partagent en quatre triangles isocèles rectangles.
On obtient le « grand carré » avec quatre autres triangles isocèles rectangles de même aire, symétriques des quatre premiers.
Télécharger la figure GéoPlan carres_vinci.2g2w
Duplication du cercle d'Archimède
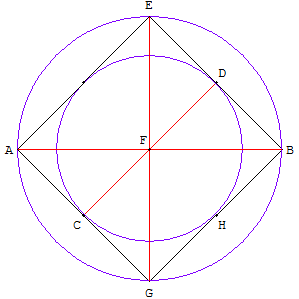
Proposition VII du livre des lemmes
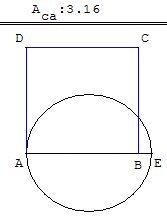
Si un cercle est circonscrit à un carré, et si un autre cercle lui est inscrit, le cercle circonscrit sera double du cercle inscrit.
Circonscrivons un cercle AB au carré AB, et inscrivons-lui le cercle CD. Que AB soit la diagonale du carré et le diamètre du cercle circonscrit.
Conduisons dans le cercle inscrit le diamètre CD parallèle au côté AE, qui est égal à CD.
Puisque le carré de AB est double du carré de AE ou de DC, et que les cercles sont entre eux comme les carrés de leurs diamètres, le cercle AB sera double du cercle CD.
Ce qu'il fallait démontrer.
Télécharger la figure GéoPlan cercles_archimedeg2w
Retrouver ces paragraphes dans : carré au collège
Voir duplication de figures : triangle, rectangle…
Problème pythagoricien du Ve siècle avant J.-C. : trouver un triangle rectangle isocèle « calculable » avec les quatre opérations des entiers.
Cela revient à trouver deux nombres naturels x et y, non nuls, tels que 2x2 = y2.
Étudier les solutions possibles selon la parité de x et y.
Si x pair et y pair en divisant les deux nombres par 2, éventuellement plusieurs fois, on obtiendrait un nombre impair, si le problème avait une solution (x, y), un des deux nombres serait impair.
Une solution dans laquelle le nombre y est impair est impossible : en effet, si y est impair, alors y2 est impair et ne peut être égal au nombre pair 2x2.
Reste le cas où x est impair et y pair. Dans ce cas, la moitié de 2x2 est impaire, alors que celle de y2 est paire : ces deux nombres ne peuvent pas être égaux.
Il n'existe donc pas de naturels (ni de rationnels) tels que 2x2 = y2. Le rapport entre le côté et la diagonale du carré est irrationnel.
Cette découverte sera alors vécue comme une catastrophe plus qu'une incitation à aller plus loin.
Cela justifiera le passage du calcul au raisonnement qui sera l'acte de naissance des mathématiques au Ve siècle.
On aurait pu penser que les Grecs, mathématiciens et philosophes découvrant la méthode axiomatique, auraient cherché à comprendre comment articuler ces nouvelles mathématiques avec les calculs plus anciens des Mésapotamiens et des Égyptiens. Au contraire, ils ont fait table rase du passé et abandonné le calcul pour le raisonnement.
Le calcul ne fut pas pour autant complément abandonné. Voir par exemple l'algorithme d'Euclide pour le calcul du PGCD ou les mathématiques du moyen-âge.
Mais il faudra attendre le XVIIe siècle, avec Descartes et la notion de coordonnées, pour la synthèse entre l'algèbre et la géométrie.
D'après Dowek Gilles – Les métamorphoses du calcul - Le pommier 2007
Duplication du cube : problème de Délos (problème déliaque) posé par les sophistes grecs au VIe siècle avant J.-C.
Construire un autel cubique, à la gloire d'Apollon, de volume deux fois plus grand que celui déjà présent dans le temple.
Le polynôme minimal du nombre 
est x3 − 2 = 0 de degré 3. est un nombre algébrique de degré 3 sur Q. Ce nombre n'est pas un nombre constructible.
La duplication du cube n'est pas possible.
Table des matières
Dans d'autres pages du site
Les Éléments d'Euclide
La Géométrie de Descartes
Téléchargement
Télécharger grands_problemes.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image,
mais Google trouve une erreur de type "soft 404".
Les copies ne devraient pas être référencées et
Google devrait choisir l'original au lieu des piratages !
Copyright 2005 - © Patrice Debart
Mobile friendly
Rétroliens (backlinks)
Les trois problèmes de l'antiquité : m@ths et tiques
Les trois grands problèmes de l'antiquité grecque : IREM de Marseille
Page no 80, créée le 14/3/2005
modifiée le 2/7/2013