Descartes et les Mathématiques

Démonstrations géométriques de Pythagore

Méthode des aires : dix figures autour de la propriété de Pythagore ;
Euclide, Pappus, Bhaskara, Léonard de Vinci, Clairaut, Garfield.

Sommaire

Théorème de Pythagore

1. Euclide

2. Démonstration de Pappus

3. Léonard de Vinci

4. Renan

5. Construction de Bhaskara

6. Garfield - Puzzle de Pythagore

7. Clairaut

8. Puzzle de Périgal

9. Triangles semblables dans un cercle

10. Triangles semblables dans un rectangle

11. Lunules d'Hippocrate

Théorème de Pythagore

Dans tout triangle rectangle, la somme des carrés des
longueurs des côtés de l'angle droit est égale au carré
de la longueur de l'hypoténuse, et réciproquement.

Le théorème de Pythagore est très populaire et tout le monde
se rappelle a² + b² = c², avec la formulation d'Euclide :
«  le carré de l'hypoténuse est égal à la somme des carrés
des deux autres côtés » que je préfère à la formulation
encyclopédique : « le carré de la longueur de l'hypoténuse,
qui est le côté opposé à l'angle droit, est égal à la somme
des carrés des longueurs des cathètes ».

Dans une tablette cunéiforme, on le retrouve à
Babylone, vers 2 000 ans avant J.-C.
Pythagore de Samos (569 - 494 avant J.-C.),
mathématicien de la Grèce antique, n'a pas découvert
ce théorème, mais l'énonçait sous forme graphique
et ne semble pas l'avoir prouvé.
Il faut attendre Euclide, vers le III^e siècle avant J.-C.,
pour la première démonstration connue.

L'américain Elisa Scott Loomis a recensé plus de 300 preuves,
ici on en présente une dizaine.

Quatre types de démonstration de Pythagore

I.   Preuve des Éléments d'Euclide, assez complexe,
qui n'est plus enseignée aujourd'hui.

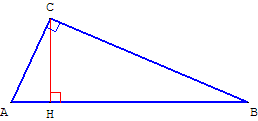
II.  Preuve utilisant la
méthode des aires grâce
à la similitude du grand
triangle rectangle ABC
avec les triangles
rectangles ACH et BCH
formés par les petits
côtés et la hauteur (CH) abaissée sur l'hypoténuse :
L'aire du grand triangle est la somme des aires des deux petits.

Pour des triangles rectangles semblables, leurs aires
sont proportionnelles aux carrés de leurs hypoténuses,
donc le carré de l'hypoténuse du grand est égal à la
somme des carrés des hypoténuses des deux petits.

III. Preuve de complémentarité basée sur des égalités
d'aire avec des manipulations sous forme de puzzle
accessible dès le cycle III de l'école primaire.

IV. Preuve arithmétique où l'on calcule les aires
de différents carrés (Bhaskara).

Réciproque du théorème de Pythagore

Les Éléments d'Euclide, livre I, proposition 48

Si dans un triangle, le carré du plus grand côté est égal à la
somme des carrés des deux autres côtés, alors ce triangle est rectangle.

Le plus grand côté est l'hypoténuse et l'angle droit
est l'angle opposé à l'hypoténuse.

Remarque : comme Euclide et pour une mémorisation plus
facile, le terme « longueur » est souvent omis dans cette page ;
chaque côté est alors assimilé à sa longueur.

1. Démonstration de Pythagore par Euclide

1.a. Éléments d'Euclide, livre I, proposition 47

Dans les triangles rectangles, le carré du côté opposé à
l'angle droit est égal aux carrés des côtés de l'angle droit.

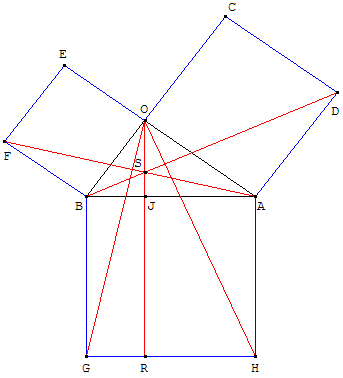
1.b. Figure dite du « moulin à vent »

Construction de trois carrés OEFB, OADC et ABGH de
côtés a, b et c à l'extérieur du triangle BOA.
Dans le cas particulier où le triangle BOA est rectangle en O,
on retrouve les démonstrations de la propriété de Pythagore
basées sur l'équivalence des figures : la somme des aires des
petits carrés est égale à celle du grand carré :
a² + b² = c².

La démonstration la plus ancienne qui soit connue du théorème
du carré de l'hypoténuse est celle qui est contenue dans les
Éléments d'Euclide et qui d'après Proclus (412-485) serait
effectivement due au géomètre alexandrin (III^e siècle avant J.-C.).

Par O menons (OR) parallèle à (BG) et traçons [OG] et [FA].

Les triangles OBG et FBA sont égaux : FBA est l'image de
OBG par la rotation de centre B et d'angle 90° (on peut
aussi vérifier que les petits côtés sont égaux à a et c,
et que les angles obtus en B sont égaux à l'angle ABO plus un droit).

Les triangles FBA et FBO ont même aire, égale à la moitié
du produit de la base FB par la hauteur OB.
Donc, 2 Aire(FBA) = FB × OB = a².
L'aire du triangle OBG est égale à la moitié du produit
de la base BG par la hauteur BJ.
Donc, 2 Aire(OBG) = BG × BJ = Aire(BGRJ).
D'où Aire(BGRJ) = a².

De même, l'étude des triangles égaux OAH et DAB permet de
montrer que : Aire(AHRJ) = b².

La somme des aires des deux rectangles précédents BGRJ et
AHRJ étant égale à c², aire du carré ABGH, Euclide démontre
bien la propriété de Pythagore :a² + b² = c².

La rotation de centre B et d'angle 90° permet de prouver que
OG = AF et que les droites (OG) et (AF) sont orthogonales.

De manière analogue OH et BD sont égaux et orthogonaux.

Le théorème de Pythagore a eu différents noms : « théorème
de la mariée » chez les Grecs, « chaise de la mariée » chez
les Hindous, « figure de l'épousée » chez les Perses pour la
réciproque, « maître de la mathématique » au Moyen-Âge,
« pont aux ânes » pour les collégiens du XIX^e siècle.

Voir : Figure de Vecten

Figure du moulin à vent avec une planche à clous, avec un carré d'aire 5

1.c. Premier théorème d'Euclide

Les éléments d'Euclide - Livre I - Proposition 47

Carré d'un petit côté du triangle rectangle

Un côté de l'angle droit est moyenne géométrique entre
l'hypoténuse et sa projection sur l'hypoténuse.

AB² = BC × BJ.

Démonstration d'Euclide

(l'aire du) carré (de diagonale) AF sera égal (à l'aire du)
parallélogramme (de diagonale) BK.

AB² = BD × DK.

Soit, en notant J le pied de la hauteur (figure du moulin à vent ci-dessus),

AB² = BC × BJ.

… Ce qu'il fallait prouver

1.d. Partage en deux d'un hexagone

À partir d'un triangle rectangle, on trace la figure dite du « moulin à vent »
et on complète en hexagone avec les traits rouges.
De combien de façons peut-on diviser cet hexagone en deux polygones
d'un seul tenant et d'aires égales en suivant les lignes tracées sur le plan ?
On précise que les trois quadrilatères hachurés
sont des carrés et que le triangle (a) est rectangle.

Solution

Il y a trois façons d'opérer.

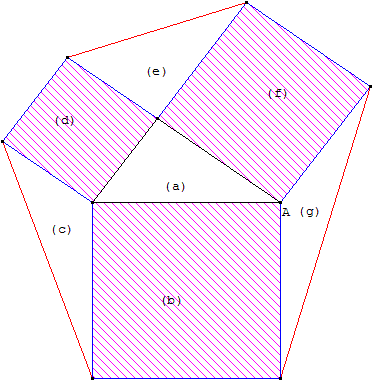
Si p et q désignent les longueurs des côtés de l'angle droit du
triangle (a), la clé consiste à remarquer, comme nous l'avons
déjà vu dans le problème des extriangles, que les quatre triangles
ont même aire, ici égale à pq/2.
Quant aux carrés, ils ont pour aires p², q², p² + q².

Le problème revient donc à obtenir deux terrains d'aire p² + q² + pq.

Le terrain contenant le carré (b) peut être composé au choix de :
    • (b), (a), (c)
    • (b), (a), (g)
    • (b), (c), (g)

D'autres solutions sont possibles pour des
configurations particulières comme q = 2p…

2. Preuve du théorème de Pythagore via Pappus

2.a. Clairaut via Pappus

Jean-Baptiste Clairaut
Mathématicien français 1713-1765.

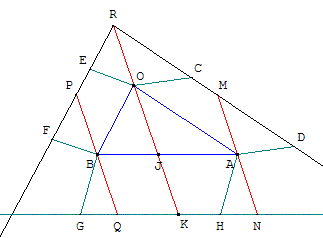
La démonstration qui suit, par glissement de parallélogrammes,
est attribuée à Clairaut, mais Montucla a écrit en 1758 dans son
« Histoire des Mathématiques » que c'est Jean Étienne Ozanam
qui l'a retrouvée chez Pappus d'Alexandrie (vers 320 après J.-C.).

Ci-dessus, figure d-un triangle BOA quelconque

2.b. Théorème de Clairaut

Soit BOA un triangle quelconque.
Si BOEF et AOCD sont des parallélogrammes
extérieurs au triangle tels que (EF) et (CD) se coupent en R.

Si, enfin, ABQN est un parallélogramme extérieur au triangle
tel que [OR] et [BQ] soient parallèles et de même longueur,
alors on a le théorème de Clairaut :
l'aire du parallélogramme ABQN est égale
à la somme des aires des deux autres parallélogrammes.

Preuve : sur les côtés d'un triangle BOA, tracer un
parallélogramme ABGH dont l'aire soit la somme de
celles de deux parallélogrammes quelconques
construits l'un sur [AO], l'autre sur [OB].

Soit AOCD et BOEF les deux parallélogrammes.
Les droites (DC) et (FE) se coupent en R.
Sur la droite (RO) qui coupe (AB) en J, prenons K tel que = .

Tout parallélogramme ABGH tel que (HG) passe par K est solution.

Les parallélogrammes AOCD et AORM, situés dans la même
bande entre les droites parallèles (OA) et (CD), ont même aire.
Les parallélogrammes AORM et KNAJ, ayant deux côtés [RO]
et [JK] de même longueur et situés dans la même
bande entre les droites (RO) et (MN), ont même aire.
De même, Aire(BOEF) = Aire(BORP) et Aire(BORP) = Aire(QKJB).

En ajoutant : Aire(AOCD) + Aire(BOEF)
    = Aire(AORM) + Aire(BORP)
    = Aire(KNAJ) + Aire(QKJB)
   = Aire(QNAB) = Aire(ABGH).

2.c. Triangle BOA rectangle

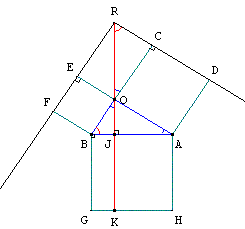
De plus, si le triangle BOA
est rectangle et si les
parallélogrammes sont des
carrés, alors on retrouve une
démonstration du théorème de P
ythagore /

OC = OA = b et
RC = OE = OB = a,
il est donc égal au triangle BOA.

CÔR = OÂB = JÔB
donc (OR) est orthogonale à (AB).

AB = RO = c et JK = RO, ABGH est un carré dont l'aire c² est la somme
des aires a² + b² des carrés AOCD et BOEF construits sur [AO] et [OB].
Pappus démontre bien la propriété de Pythagore :

a² + b² = c².

2.d. Puzzle chinois

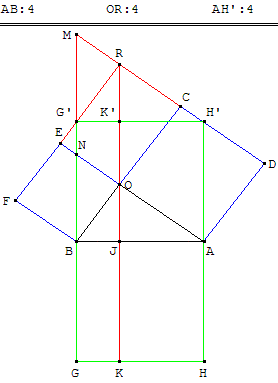
Nassir ad-Din at Tusi (1201-1274)

Soit R le point d'intersection
des droites (CD) et (EF).
Soit (OJ) est une hauteur de
BOA prolongée jusqu'en K.

EOCR est un rectangle,
le triangle rectangle RCO
a pour côtés de l'angle
droit RC = a et OC = b.
Le triangle RCO est
donc égal à BOA :
RO = AB = c.

Ce triangle est
semblable à BJO.
Les angles RÔC
et JÔB sont égaux,
les points R, O, J et K
sont alignés.

La droite (BG) coupe
(EF) en G’. BORG’, ayant ses côtés parallèles deux à deux, est
un parallélogramme et BG’ = OR = c. L'aire est égale au produit
de la base OB par la hauteur OE :
Aire(BORG’) = OB × OE = a².
Cette aire est aussi égale au produit de la base OR par la hauteur BJ :
Aire(BORG’) = OR × BJ = c × BJ = Aire(BJKG).

De même, la droite (AH) coupe (CD) en H’.
AORH’ est un parallélogramme et AH’ = OR = c.
Aire(AORH’) = OA × OC = b².
Aire(AORH’) = OR × AJ = c × AJ = Aire(AJKH).

On a donc a² + b² = Aire(BJKG) + Aire(AJKH)
    = Aire(ABGH) = c².

Variante 1 : utiliser les rectangles du grand carré supérieur :
Aire(BJK’G’) = a² ; Aire(AJK’H’) = b².
a² + b² = Aire(BJK’G’) + Aire(AJK’H’)
    = Aire(ABG’H’) = c².

Variante 2 (J.J.I. Hoffmann – 1821) :
Soit M le point d'intersection de (BG’) et (CD).
On a Aire(BORG’) = Aire(NORM) = a²,
on sait que Aire(OAH’R) = b²,
donc a² + b² = Aire(NORM) + Aire(OAH’R)
   = Aire(NAH’M).
Cette dernière aire est égale au produit de la base AH’ par la hauteur AB :
Aire(NAH’M) = AH’ × AB = c².

On a bien la relation de Pythagore : a² + b² = c²

3. Preuve de Pythagore
par Léonard de Vinci (1452-1519)

Tempelhoff - Anfangsgründen der Geometrie - Berlin 1769
Terquem - Nouveau manuel de géométrie - Paris 1838

On reprend la figure d'Euclide et on construit
sur [GH] un triangle rectangle ZGH égal à OAB.

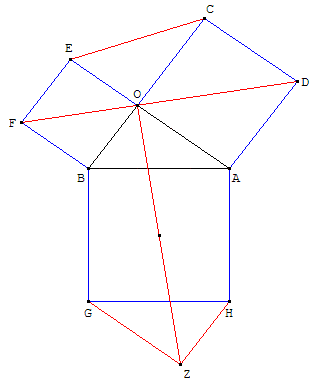
On mène [OZ], [EC], [OF] et [OD].
La somme des angles en O situés d'un même côté de DOF
est égale à un plat. Les points F, O et D sont alignés.

Démonstration 1

Les hexagones BFECDA et BOAHZG sont équivalents,
car ils sont constitués de quadrilatères égaux, FECD
et OBGZ, FBAD et ZHAO ; FECD et FBAD sont
symétriques par rapport à (FD), OBGZ et ZHAO
sont symétriques par rapport au centre du carré ABGH ;
par la rotation de centre B et d'angle 90°.
Aire(OBGZ) = Aire(FBAD) ;
en effet, BO = BF, BG = BA, CZ = AD et les angles OBG = FBA et ECD = BAD.

Or si à chacun des hexagones considérés plus haut nous
retranchons deux fois l'aire du triangle ABC
nous obtenons respectivement a² + b² et c².
On a donc a² + b² = c².

Démonstration 2

La rotation de centre B et d'angle 90° transforme O en F,
envoie [BG] sur [BA], BGZ sur BAD et [GZ] sur [AD],
donc OBGZ sur FBAD.
De là, Aire(OBGZ) = Aire(FBAD).
En ôtant l'aire du triangle OAB de chaque membre,
on a donc a² + b² = c².

Démonstration 3

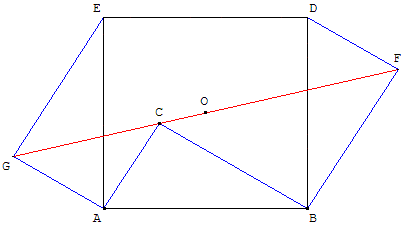
Par un retournement de l'hexagone du bas de la figure précédente,
on obtient une autre démonstration due à  Nassir-Ed-Din :

À partir d'un triangle ABC, rectangle en C, on construit,
par une rotation r de centre A et d'angle 90°,
le triangle AEG, et par une rotation r’ de centre B
et d'angle − 90°, le triangle DBF.

AB = AE = BD = c, EÂB = ABD = 90° : ABDE est un carré.

C a pour image G et F par les rotations r et r’. Les triangles CAG et CBF
sont rectangles isocèles. Les angles GCA et BCF mesurent 45°.
En ajoutant ces angles à l'angle droit ACB, on trouve que GCF = 180°.
Cet angle est plat, les points G, C et F sont alignés.

Par la rotation r’^{– 1} de centre B et d'angle 90°, DBF a pour image
ABC, par r ABC a pour image AEG.
DBF a donc pour image AEG par la composée de deux rotations
d'angles 90°, c'est une rotation d'angle 180°, donc une symétrie s.
Cette symétrie transforme D en A. Cette symétrie a pour centre O
le milieu du carré. Par la symétrie s,
F a pour image G, et le point O appartient à la droite (FG). O est

le centre de symétrie de l'hexagone ABFDEG;
et la droite (FG) le partage en deux parties d'aires égales.

Les triangles rectangles ont pour aire vab.
L'hexagone ABFDEG formé du carré et de
deux triangles rectangles a pour aire c² + ab.
Le quadrilatère moitié ABFG a pour aire (c² + ab).
Ce quadrilatère est formé des triangles rectangles GAC, ABC et CBF.
La somme des aires est égale à b² + ab + a².
Après simplification de ces deux expressions
de l'aire de ABFG, on retrouve c² = a² + b².

4. Pythagore par Renan

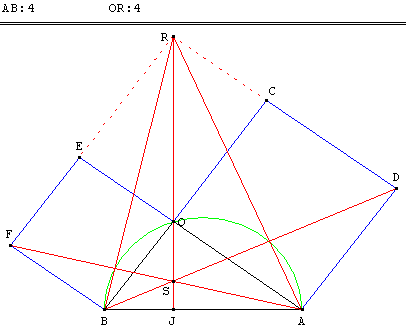
Soit R le point d'intersection de la perpendiculaire à (AF)
issue de B et la perpendiculaire (OJ) à (AB) issue de O.

Les triangles ABF et ROB ont leurs côtés perpendiculaires deux à deux.
Les côtés BF et OB ont même longueur. Ces deux triangles sont donc égaux :
Aire(ABF) = Aire(ROB) et OR = AB = c.

On a montré au paragraphe 1. Euclide que :
Aire(ABF) = FB × OB = a² d'où Aire(ROB) = RO × BJ = a².

De même, la perpendiculaire à (BD) issue de A coupe (OJ) en R.
Les triangles BAD et ROA sont égaux et on a :
Aire(BAD) = b² d'où Aire(ROA) = RO × JA = b².

On en déduit que :
a² + b² = Aire(RBO) + Aire(ROA) = RO × (BJ + JA) = RO × BA = c².

D'où la relation de Pythagore a² + b² = c².

Figure de Vecten : homothéties pour montrer que S
est le point de concours des droites (OR), (AF) et (BD) :
voir carrés autour d'un triangle BOA

5. Construction de Bhaskara

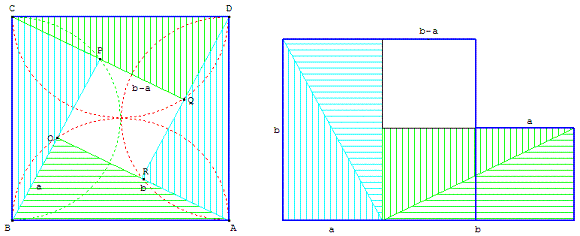
Puzzle : Babylone, XVII^e siècle avant J.-C. -
Chine époque Han, Liu Hui, III^e siècle - Inde, Bhaskara, XII^e siècle.

Quatre triangles rectangles, de côtés a, b (b>a)
et d'hypoténuse c, sont assemblés.
Leurs hypoténuses formant un grand carré ABCD.
Il apparaît au centre un carré OPQR de côté b − a.

En associant deux à deux les triangles dans
la figure de droite, puis le carré central,
on obtient une surface décomposable
en deux carrés, l'un de côté b, l'autre de côté a.

D'où la relation de Pythagore c² = a² + b², que l'on peut aussi calculer ainsi :
l'aire du grand carré ABCD de côté c est égale à la somme des aires de
quatre triangles rectangles et de l'aire du petit carré OPQR de côté b − a.
c² = 4 ( ab) + (b − a)²,
soit c² = 2ab + a² − 2ab + b².

Construire un carré de côté b–a : carré au collège

6.a. Le problème du président
James Abraham Garfield

Président des États-Unis né en 1831 – assassiné en 1881.

Construction d'un triangle rectangle ADE
égal au triangle rectangle ABC

Attribuée à Paul Painlevé (1863-1933),
homme politique mais aussi mathématicien,
cette construction remonte en fait au
mathématicien italien Mascheroni (1750-1800)
connu pour ses résolutions de problèmes à la règle et au compas.
L’Histoire dit que Bonaparte, excellent élève en math,
en proposa une démonstration devant l’Académie des sciences.

James Garfield publia sa démonstration en 1976
dans le New England Journal of Education.

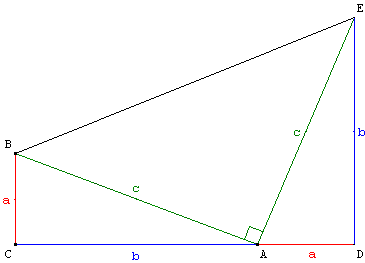
La figuire ci-dessus représente un trapèze
rectangle formé de trois trois triangles ractangle.
On calcule l'aire S de ce trapèze CDEB de deux manières :
    – Soit en additionnant les aires des trois triangles rectangle;
le double de l'aire ab des deux triangles ABC ou ADE et l'aire c²
du triangle rectangle isocèle ABE, aire moitié de celle du carré de côté c.
On a S = 2 × ab + c².

    – Soit avec la formule de l'aire du trapèze rectangle :
le produit de la moyenne des bases (b+a) par sa hauteur CD = a+b.
On a S = (b+a) (a+b) est égale à deux
aires du triangle rectangle ABC plus l'aire de ABE.

D'où 2 × ab + c² = (a+b)², donc 2ab + c² = (a+b)².

Et finalement en simplifiant 2ab, on a la propriété de Pythagore c² = a² + b².

Trigonométrie pythagoricienne - Serge Perrine

6.b. Les quatre triangles - Puzzle chinois

Chou Pei Suan Ching, vers 200 avant J.-C.

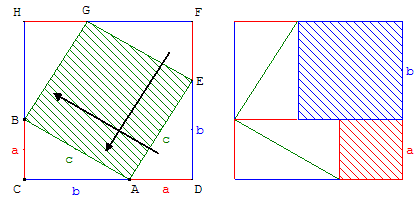
En dupliquant la figure précédente, par une symétrie
de centre O milieu de [BE], on obtient le puzzle chinois.

La démonstration est attribuée à Simson,
mathématicien écossais (1687-1768).

Figure de gauche : construction de quatre triangles rectangles
égaux au triangle rectangle ABC sur les bords
à l'intérieur d'un grand carré de côté a+b.
Les hypoténuses forment un carré, hachuré en vert, de côté c.
L'aire du grand carré est donc égale à l'aire hachurée c²,
plus quatre fois l'aire du triangle rectangle.

Figure dz droite : en faisant glisser deux triangles on obtient
à l'intérieur d'un grand carré, de côté a+b, deux carrés hachurés
de côtés a et b, complétés par quatre triangles rectangles,
égaux au triangle ABC, formant deux rectangles de longueurs a et largeurs b.
L'aire du grand carré est donc égale à l'aire hachurée a² + b²,
plus quatre fois l'aire du triangle rectangle.

Conclusion :
Les aires hachurées des deux figures sont égales et on a c² = a² + b².

6.c. Application : trois carrés contigus

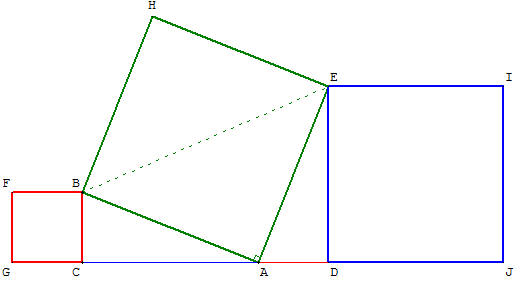
BCGF, ABHE et DEIJ sont des carrés.

Monter que :

  • les triangles rectangles ABC et EAD sont isométriques,

  • l'aire du carré ABHE est égale à la somme des aires
            des carrés BCGF et DEIJ.

7. Thabit Ibn Qurra

7.a. Clairaut

Figure de Thabit Ibn Qurra, mathématicien arabe du IX^e siècle,
né à Harran (Mésopotamie) en 826, mort à Bagdad en 901.
Inde védique – Chine des Han.
Publié en 1741 – Éléments de géométrie – Alexis Clairaut.

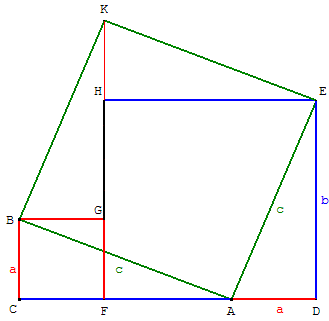
Configuration 1 : construction de deux
carrés BCFG et DEHF
de côtés a et b contenant deux triangles
rectangles ABC et EDA égaux.

Configuration 2 : on fait pivoter les deux triangles rectangles :
BCA autour de B vient en BGK et EDA autour de E
vient en EHK. On obtient un carré ABKE de côté c.

Les deux configurations sont formées de
deux triangles rectangles et du polygone ABGHE.
L'aire a² + b² de la première configuration
est égale à l'aire c² de la deuxième configuration.

7.b. Le Puzzle de Pythagore carré

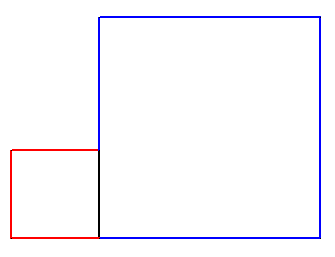
On donne deux carrés accolés comme l'indique la figure ci-dessus.
Former un grand carré en deux coups de
ciseaux et un nouvel assemblage des pièces.

7.c. Le Puzzle carré (Lui Hui, chine III^e siècle)

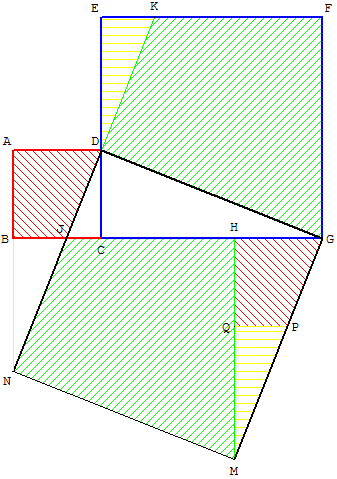
Autre solution en cinq pièces

À partir d'une plaque de carton CDEHGB
constituée d'un grand carré accolé d'un petit,
comme l'indique la figure ci-dessus, on veut
découper les pièces
d'un puzzle qui permettra de reconstituer un
autre carré (plus grand que les deux premiers).

Comment réaliser ce puzzle avec seulement
deux découpes rectilignes du carton ?

Solution en trois pièces

Figure ci-dessus : placer A sur [FD] tel que
AD = a et couper suivant [AB] et [AE].

Une autre solution en quatre pièces ci-contre :

Découper la plaque BGFEDA selon(DJ),
la perpendiculaire en D à [DG] et selon [DG].

8. Puzzle de Périgal

Perigal, Henry
Mathématicien anglais (1801-1898)

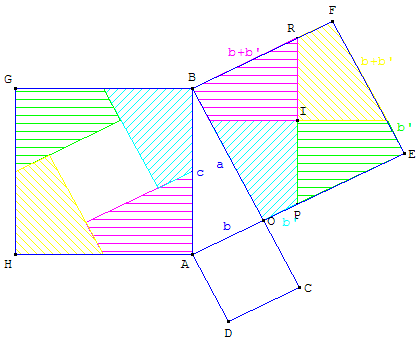
8.a. Découpage de carrés

BOA est un triangle rectangle en O, de côtés a, b (b>a) et d'hypoténuse c.

On découpe le carré moyen BOEF par une parallèle
et une perpendiculaire à l'hypoténuse passant par le centre I du carré.

On obtient quatre quadrilatères superposables que l'on fait glisser,
par translations, dans le grand carré ABGH. L'emplacement central,
laissé libre, est exactement égal au petit carré AOCD.

Le grand carré est recouvert avec cinq pièces issues des deux autres.

8.b. Puzzle de Pythagore en cinq pièces

Avec les quatre quadrilatères et le petit carré central,
on obtient un puzzle de cinq pièces qui permet d'obtenir :
  • ou bien le grand carré de gauche,
  • ou bien deux petits carrés (à droite).

Preuve : les quatre quadrilatères découpés sont
superposables puisque I est centre de symétrie.
La figure APRB ayant ses côtés opposés
parallèles est un parallélogramme.
BR = AP = AO + OP = b + b’.

Les quadrilatères ont donc pour grand côté b + b’ et petit côté b’.
L'emplacement central a pour côté la différence qui est b.
Par les translations le parallélisme est conservé,
le centre est donc un carré de côté b.

Voir : puzzle et carrés

9. Triangles semblables dans un cercle

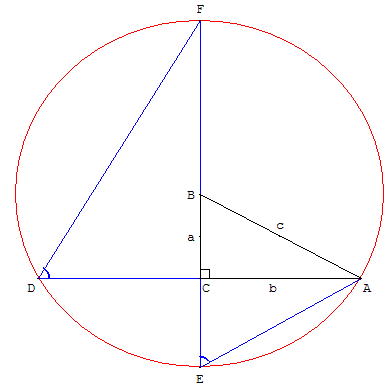
ABC est un triangle rectangle en C.

Le cercle de centre B passant par A coupe (BC)
en E et F (CE < CF) et recoupe (CA) en D.

Les angles inscrits ADF et AÊF sont égaux.
Dans les triangles rectangles FCD et ACE,
semblables, le calcul de tan(ADF) et de tan(AÊF) donne l'égalité :

,

d'où CF × CE = CA × CD (on retrouve l'opposé
de la puissance du point C par rapport au cercle).

Avec CF = c + a, CE = c − a et CA = CD = b,
l'égalité s'écrit (c + a)(c − a) = b².

On retrouve c² = a² + b².

On obtient aussi l'égalité CF × CE = CA²
avec le théorème de Thalès suisse dans le triangle EFA,
inscrit dans un demi-cercle,
rectangle en A et de hauteur AC :
la hauteur issue de l'angle droit est la moyenne géométrique
entre les projections des petits côtés sur l'hypoténuse.

10. Triangles semblables dans un rectangle

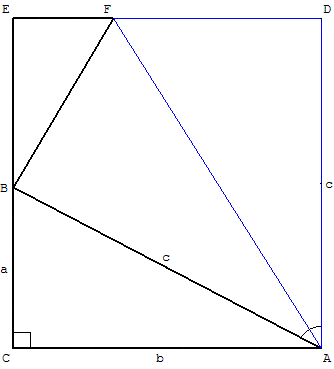
À partir du triangle ABC rectangle en C, on construit le rectangle CADE
tel que la longueur AD soit égale à l'hypoténuse AB = c.
La bissectrice (AF) de DÂB rencontre [ED] en F.

Comme AB = AD, la droite (AF) est axe de symétrie du quadrilatère ADFB.
En posant EF = x on a FB = FD = b − x.
Par symétrie l'angle ABF, égal à ADF, est droit.

Les angles aigus CAB et EBF ayant leurs côtés perpendiculaires sont égaux.
Les triangles rectangles ABC et BFE sont semblables.

Le calcul de tan(FBE) et de tan(BÂC) donne l'égalité : .
On a donc , c'est-à-dire x = .

Une autre égalité avec sin(FBE) et sin(BÂC) :.
On a donc , c'est-à-dire x = .

Dès lors, = .
En simplifiant par a, le calcul des « extrêmes » et des « moyens »
permet de retrouver la propriété de Pythagore ; c² − a² = b².

11. Lunules

Lunule (féminin) : portion de surface délimitée par
deux cercles non concentriques de rayons différents,
formant un croissant de lune en forme de ménisque :
convexe d'un côté et concave de l'autre.

Segment circulaire : portion de surface comprise
entre un arc de cercle et la corde qui le sous-tend.

Le théorème des deux lunules est un ancien théorème
de géométrie démontré par Hippocrate de Chios.
Les deux lunules sont aussi appelées lunules d'Hippocrate.

11.a. Lunules d'Hippocrate de Chios

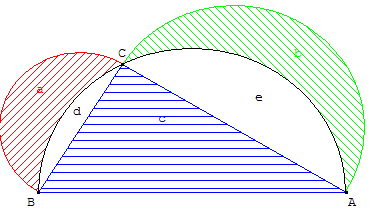
Soit ABC un triangle rectangle en C et (Γ)
le disque de diamètre [AB] circonscrit à ABC.

La lunule a est formée par le demi-disque
de diamètre [BC] extérieur au triangle ABC,
auquel en enlève son intersection avec (Γ) :
le segment circulaire d.

La lunule b est la figure formée par le
demi-disque de diamètre [AC] extérieur au triangle ABC,
auquel en enlève son intersection avec (Γ) : le segment circulaire e.

Théorème des deux lunules :
La somme des aires des deux lunules est égale à l'aire du triangle rectangle ABC.

C'est la « quadrature » des lunules prouvée
au V^e siècle avant J.-C. par Hippocrate de Chios.

Il pensait que la quadrature de ses lunules allait le rapprocher
de la résolution de la quadrature du cercle.

11.b. Théorème de Pythagore généralisé

Le théorème de Pythagore peut être généralisé au cas de figures semblables :
trois figures semblables étant construites sur les trois côtés d'un
triangle rectangle,
l'aire de celle construite contre l'hypoténuse
est égale à la somme des aires des deux autres.

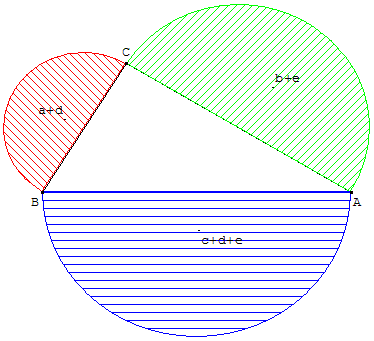
Dans l'exemple ci-dessus, la somme des aires des demi-disques
de diamètres [AC] et [BC] est égale à l'aire du demi-disque de diamètres [AB].

En nommant les aires comme ci-contre, on a :

(a + d) + (b + e) = c + d + e.

En simplifiant par d + e l'égalité précédente, on obtient l'égalité :

a + b = c,

d'où le théorème des deux lunules.

Voir : quatre lunules d'Hippocrate : la quadrature du cercle

    aire maximum de deux lunules

    aire formée par deux segments circulaires

Table des matières

Index triangles

Dans d'autres pages du site

La constante de Pythagore dans une tablette babylonienne

Puissance d'un point par rapport à un cercle :
retrouver le théorème de Pythagore sans les aires

Longueur d'une diagonale du parallélépipède rectangle

Carré au collège - somme ou différence des aires de deux carrés :
    Sulbasutras
    Puzzle de Gougu

Carrés autour d'un triangle BOA

Le triangle rectangle

La géométrie du triangle

Google friendly, sur ordinateur, cette page en grand écran

La première page de ce document n'est pas une image
et ne devrait pas être référencée comme telle par Google !

Copyright 2003 - © Patrice Debart